原题链接：

456. 132 模式

https://leetcode.cn/problems/132-pattern/description/

完成情况：

解题思路：

	/**
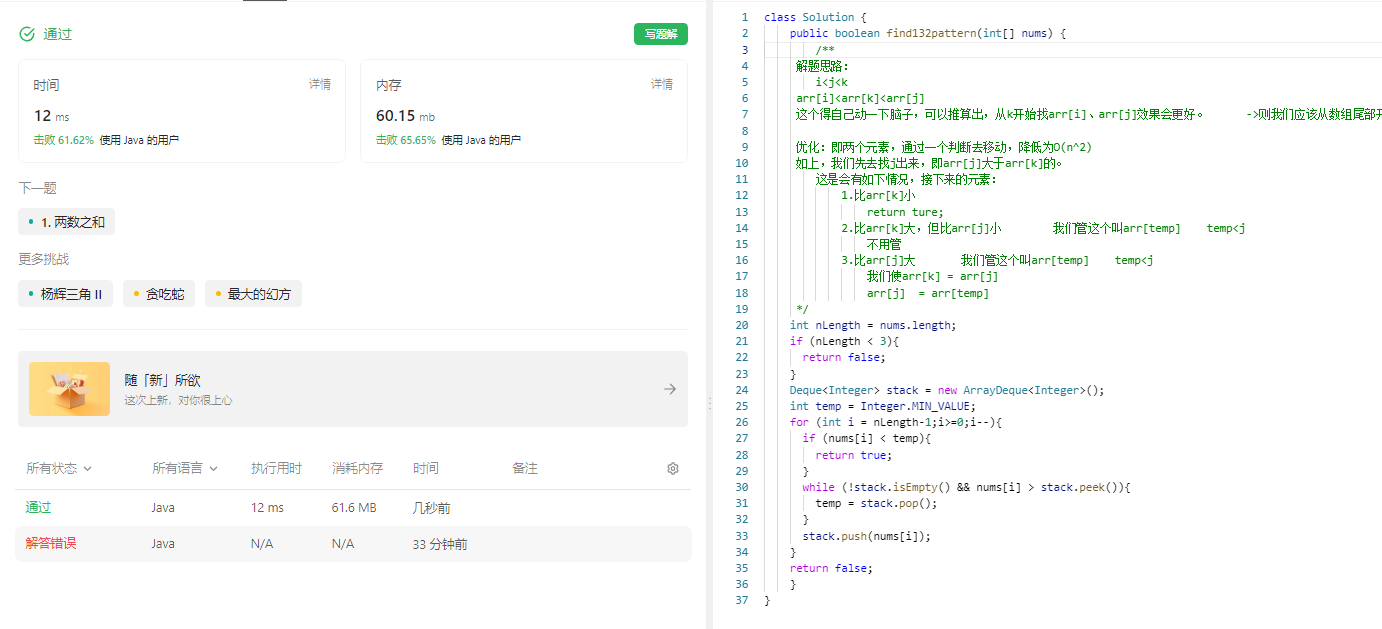
	 解题思路：
	    i<j<k
	 arr[i]<arr[k]<arr[j]
	 这个得自己动一下脑子，可以推算出，从k开始找arr[i]、arr[j]效果会更好。      ->则我们应该从数组尾部开始遍历

	 优化：即两个元素，通过一个判断去移动，降低为O(n^2)
	 如上，我们先去找j出来，即arr[j]大于arr[k]的。
	    这是会有如下情况，接下来的元素：
	        1.比arr[k]小
	            return ture;
	        2.比arr[k]大，但比arr[j]小        我们管这个叫arr[temp]    temp<j
	            不用管
	        3.比arr[j]大       我们管这个叫arr[temp]    temp<j
	            我们使arr[k] = arr[j]
	            arr[j]  = arr[temp]
	 */

参考代码：

package 西湖算法题解___中等题;

import java.util.ArrayDeque;
import java.util.Deque;
import java.util.Stack;

public class __454是否有132模式__单调栈 {
	public boolean find132pattern(int[] nums) {
		/**
		 解题思路：
		    i<j<k
		 arr[i]<arr[k]<arr[j]
		 这个得自己动一下脑子，可以推算出，从k开始找arr[i]、arr[j]效果会更好。      ->则我们应该从数组尾部开始遍历

		 优化：即两个元素，通过一个判断去移动，降低为O(n^2)
		 如上，我们先去找j出来，即arr[j]大于arr[k]的。
		    这是会有如下情况，接下来的元素：
		        1.比arr[k]小
		            return ture;
		        2.比arr[k]大，但比arr[j]小        我们管这个叫arr[temp]    temp<j
		            不用管
		        3.比arr[j]大       我们管这个叫arr[temp]    temp<j
		            我们使arr[k] = arr[j]
		            arr[j]  = arr[temp]
		 */
		int nLength = nums.length;
		if (nLength < 3){
			return false;
		}
		Deque<Integer> stack = new ArrayDeque<Integer>();
		int temp = Integer.MIN_VALUE;
		for (int i = nLength-1;i>=0;i--){
			if (nums[i] < temp){
				return true;
			}
			while (!stack.isEmpty() && nums[i] > stack.peek()){
				temp = stack.pop();
			}
			stack.push(nums[i]);
		}
		return false;
	}
}

单调栈

单调栈（Monotonic Stack），也叫做单调递增栈或单调递减栈，是一种特殊类型的栈数据结构。它主要用于解决一些与序列中元素的单调性有关的问题，如寻找下一个更大的元素、寻找前一个更大的元素等。

单调栈的特点在于，栈中的元素保持特定的单调性（递增或递减）。当新的元素要入栈时，会先将栈中所有不满足单调性要求的元素出栈，然后再将新元素入栈。这样可以保证栈内元素始终保持单调性，从而能够在栈中高效地找到某些与单调性相关的信息。

常见的应用场景包括：

1. 寻找下一个更大（或更小）元素：对于一个序列中的每个元素，需要找到在该元素右边第一个比它更大（或更小）的元素。单调栈可以帮助高效地解决这类问题。

2. 柱状图中的最大矩形面积：给定一个柱状图，找到可以画出的最大矩形的面积。这个问题可以通过单调递增栈来解决。

3. 滑动窗口的最大值：给定一个数组和一个固定大小的窗口，窗口从数组的最左边滑动到最右边，需要找到每个窗口中的最大值。

4. 删除数组中的元素以获得单调数组：给定一个数组，通过删除一些元素，使得剩余元素形成一个单调递增或单调递减的数组。

等等。

单调栈的思想在解决这些问题时能够以较低的时间复杂度实现，因为它可以避免重复计算，只保留有用的信息。无论是单调递增栈还是单调递减栈，其基本操作都是入栈和出栈，通过这些操作来维护单调性，从而解决各种相关问题。