---

前言

直方图操作是图像处理中的一个基本工具，直方图计算简单，适合于快速硬件的实现，基于直方图的技术成为实时图像处理的一个流行工具。

在了解直方图进行图像处理前先明确几个概念：

• 直方图容器：细分的灰度级称为直方图容器，个人理解：容器顾名思义是容纳一类事物的东西，直方图容器就是容纳灰度级的；
• 直方图或图像直方图：通常把处理的归一化直方图简单称为直方图或图像直方图

---

一、直方图为什么可以进行图像处理？

直方图的形状与图像的外观有关。

如下图显示了具有4个基本灰度特性的几幅图像：暗图像(左上)、亮图像(右上)、低对比度图像(左下)和高对比度图像(右下)。

下图分别是这几幅图像的归一化直方图：

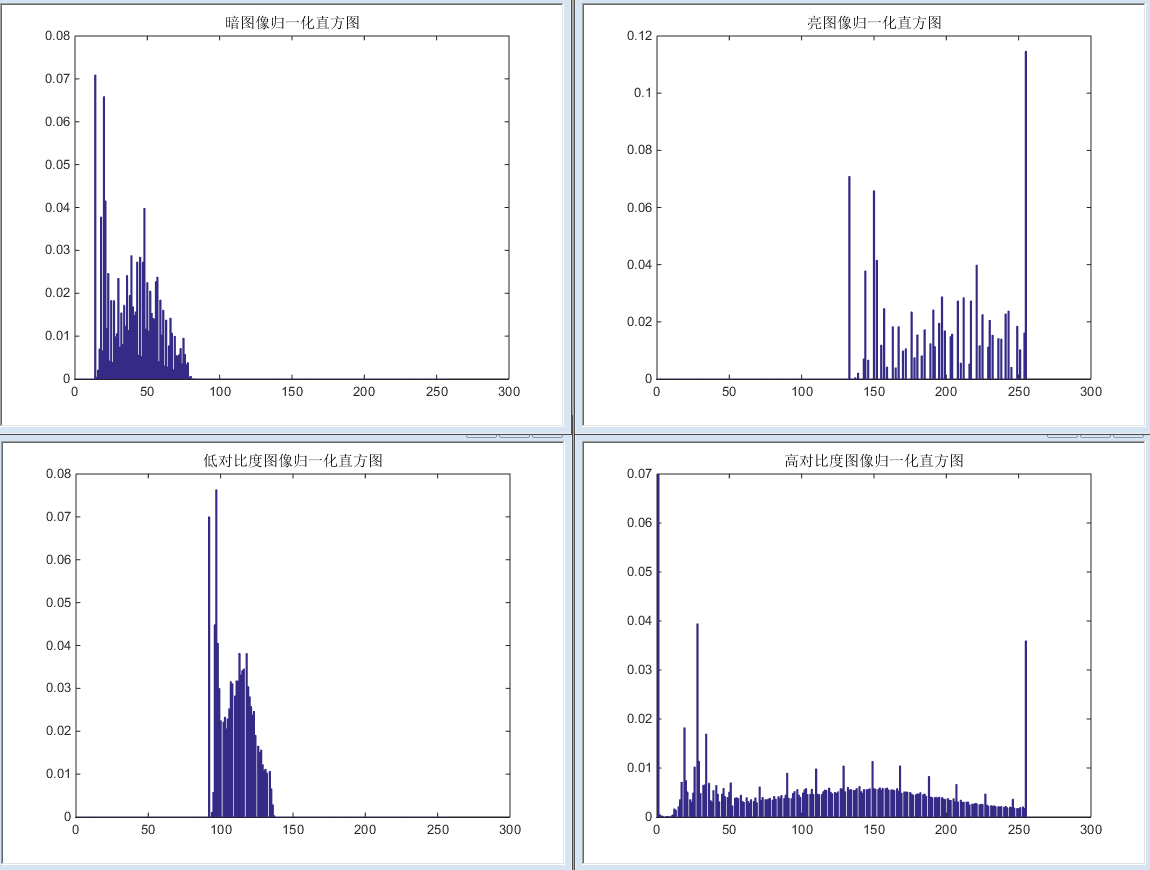
从归一化直方图中我们可以得出这几个结论：

• 暗图像的直方图中，大多数直方图容器集中在灰度级的低端/暗部；
• 亮图像的直方图中，大多数直方图容器集中在灰度级的高端/亮部；
• 低对比度图像的直方图中，直方图容器基本位于灰度级的中间；对于单色图像来说，这表示图像具有灰色的外观；
• 高对比度图像的直方图中，直方图容器覆盖了较宽范围的灰度级，并且像素的分布也基本上是均匀的，直方图容器的高度基本相同。

可以简单的得出结论：像素占据整个灰度级范围并且均匀分布的图像，将具有高对比度的外观和多种灰色调。最终呈现的图像效果将是显示了大量灰度细节并具有高动态范围。

另外，直方图可以表达更多的信息，比如，物体的颜色分布、物体的边缘梯度模板或是以概率分布的形式表达当前对物体位置的估计。

直方图可以说是计算机视觉领域中的经典工具之一。

例如，通过判断帧与帧之间边缘和颜色的统计量是否出现巨大变化，来检测视频中场景的变换。

通过使用兴趣点邻域内的特征组成的直方图，来辨识兴趣点。若将边缘、颜色、角点等等的直方图作为特征，可以使用分类器来进行目标识别。

提取视频中的颜色或边缘直方图序列，可以用来判断视频是否拷贝自网络。

直方图是一种用来揭示数据分布的统计特性的工具。

---

二、直方图处理怎么实现？

基础的直方图处理有：直方图均衡化、直方图规定化、局部直方图处理、直方图统计量增强图像等。

直方图均衡化

具体理论基础参考《数字图像处理（第四版）》冈萨雷兹版3.3.1节P87。

直方图均衡化的计算公式：
$$s_k=T(r_k)=(L-1)\sum _{j=0}^k{p}_r(r_j)=\frac{L-1}{MN}\sum _{j=0}^k{n}_j$$
其中$r_k$是输入图像的灰度值，通常$r_k=k$，$k=0,1,2,...L-1$；$s_k$是$r_k$对应的输出图像灰度值；$L$是图像的灰度级，比如$8bit$图像灰度级为$255$；$MN$是图像像素总数；$n_j$表示灰度值为$r_k$的像素数量。

直方图均衡化视会常事产生一幅具有均匀直方图的输出图像，希望自动增强图像时，直方图均衡化是很好的选择。

---

直方图匹配-规定化

具体理论基础参考《数字图像处理（第四版）》冈萨雷兹版3.3.2节P92。

用于生成具有规定直方图的图像的方法，称为直方图匹配或直方图规定化。

直方图规定化需要有一幅图像，这幅图像的直方图即为规定的直方图，将输入图像经过某种转换，得到输出图像，使得输出图像的直方图与规定的直方图一致或者大致相同。

离散直方图规定化的过程总结如下：

1. 计算输入图像的直方图，并将利用式将(1)输入图像中的灰度映射到直方图均衡化后的图像中的灰度，将得到的值$s_k$四舍五入到整数区间$[0,L-1]$；
2. 由规定的直方图值$p_z$，用式$G(z_q)=(L-1){\sum }_{i=0}^q{p}_z(z_i)$ 计算$G(z_q)$的所有值，将得到的值四舍五入到区间$[0,L-1]$内的整数，将四舍五入后的$G(z_q)$值存储到一个查找表中；
3. 找到$s_k$与$G(z_q)$最接近时对应的$z_q$值，存储从$s$到$z$的映射；当多个$z_q$值有相同的匹配时，按照约定选择最小值；
4. 根据步骤3中找到的映射，将每个均衡化后的像素$s_k$值映射到直方图规定化图像中值为$z_q$的对应像素，形成直方图规定化后的图像。

---

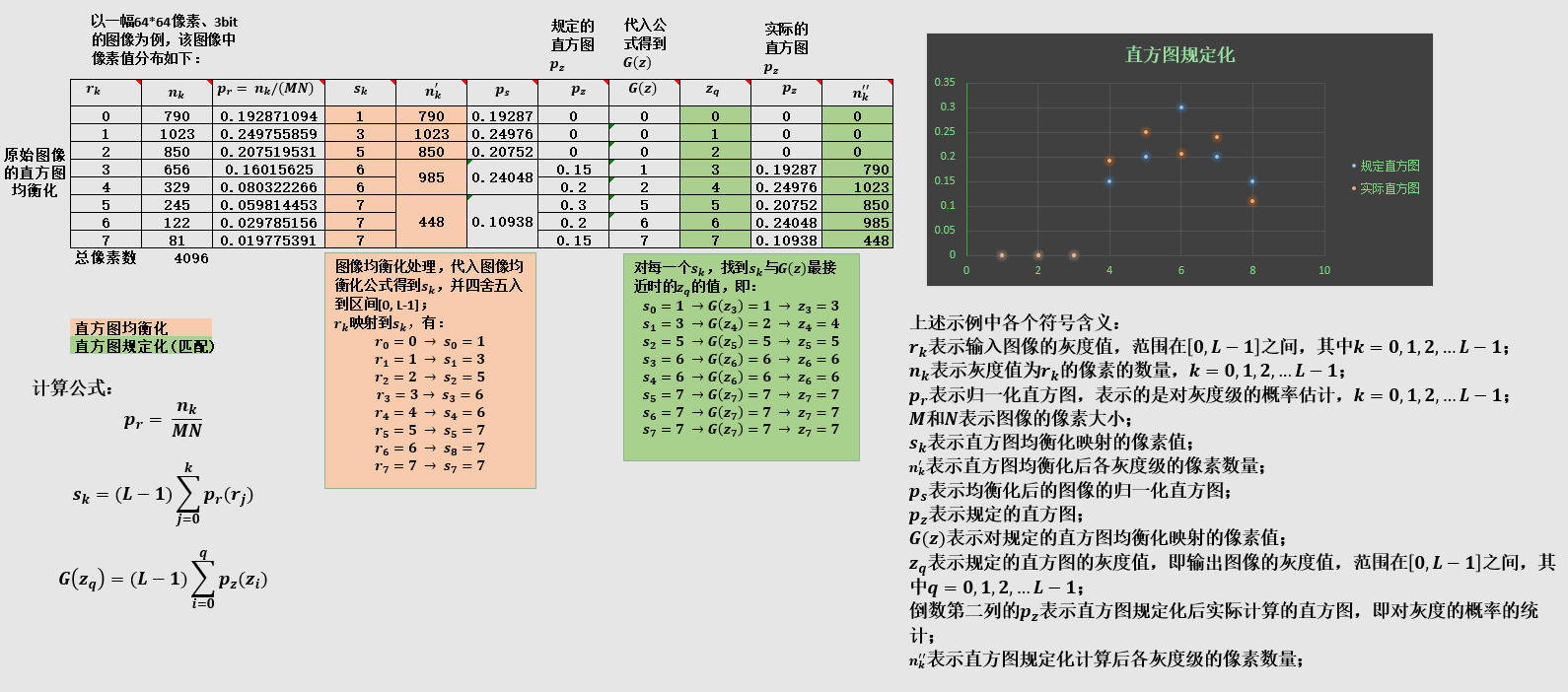
如下以一个简单的示例展示了直方图均衡化和直方图规定化的原理。

上图的表格中展示了直方图均衡化以及直方图规定化过程中的计算数据；表格上下文字是对过程的描述；右上图表中展示了规定直方图与规定化实际计算的直方图，从这里可以看出实际计算的结果与规定直方图并不完全匹配，但是实现了将灰度向灰度级的高端移动的一般趋势。

具体文件链接：
链接1；
链接2 提取码：ci06；

---

局部直方图处理

当需要增强图像中几个小区域的细节时，通常采用基于像素邻域的灰度分布的变换函数进行局部增强。

局部直方图处理的过程大致是：定义一个邻域，并将其中心在水平方向或垂直方向上从一个像素移动到另一个像素；在每个位置，计算邻域中的各点的直方图，得到直方图均衡化或直方图规定化变换函数；这个函数用于映射邻域中心像素的灰度；然后将邻域的中心移到一个相邻像素位置，并重复这个过程。

---

直方图统计量增强图像

直方图统计量增强图像的主要思路是计算图像的均值和方差，根据邻域像素的均值和方差判断中心像素是否需要增强，如果需要，则根据给定的灰度变换函数增强该像素。

均值是平均灰度的测度，方差是图像对比度的测度。

使用局部均值和方差处理图像的一个重要优点是，根据这些与图像外观紧密相关的统计测度可以开发处简单且强大的增强规则；

如下是根据直方图统计量增强图像的一种方法：

1. 确定某个区域在点$(x,y)$处是相对较亮还是较暗的方法：将局部灰度均值$m_{s_{xy}}$与全局灰度均值$m_G$进行比较，如果$k_0{m}_G\le m_{s_{xy}}\le k_1{m}_G$，则将$(x,y)$处的像素作为待处理的候选像素；其中$k_0$和$k_1$是非负常数，且$k_0\le k_1$。比如，如果关注区域是比平均灰度的$1/4$更暗的区域，那么选择$k_0=0$和$k_1=0.25$。

2. 增强低对比度的区域，确定某个区域的对比度是否使得它是一个增强的候选区域的方法：将局部灰度方差${\sigma }_{s_{xy}}$与全局灰度方差${\sigma }_G$比较，若$k_2{\sigma }_G\le {\sigma }_{s_{xy}}\le k_3{\sigma }_G$，则考虑将$(x,y)$处的像素作为候选像素；其中$k_2$和$k_2$是非负常数，且$k_2<k_3$。比如，要增强对比度较低的一个暗色区域，可以选择$k_2=0$和$k_3=0.1$。

3. 满足上面所有局部增强的候选像素按照如下方式处理：乘以一个规定常数$C$，增大或减小其相对于图像剩下部分的灰度值，不满足增强条件的像素则保持不变；

上面方法总结为公式如下：
$$g(x,y)=\{\begin{array}{cc}Cf(x,y),& k_0{m}_G\le m_{s_{xy}}\le k_1{m}_{G}AND{k}_2{\sigma }_G\le {\sigma }_{s_{xy}}\le k_3{\sigma }_G\\ f(x,y)& 其他\end{array}$$
其中，$x=0,1,2,...,M-1$，$y=0,1,2,...N-1$，$C、k_0、k_1、k_2和k_3$是规定的常数$，$$m_G$是输入图像的全局均值，${\sigma }_G$是输入图像的标准差，参数$m_{s_{xy}}$和${\sigma }_{s_{xy}}$分别是局部均值和局部标准差，在每个$(x,y)$位置都会变化，$M$和$N$是输入图像中的行数和列数。

从上面的叙述中可以知道，$k_0、k_1、k_2、k_3、C$等参数的选择很重要，

---

三、OpenCv提供的直方图基础操作

直方图均衡化

扩大图像的动态范围以增强对比度最常用的技术是直方图均衡化。

解决扩展分布值的问题的一个较好的方法是重映射函数是累积分布函数，这也是直方图均衡化的原理。

OpenCv提供函数cv::equalizeHist()用于直方图均衡处理，要注意，该函数只能处理$8bit$一维图像，并且输出也是$8bit$一维图像；如果要处理的是彩色图像，需要分通道逐一处理。

函数声明：

void cv::equalizaHist(
    const cv::InputArray src,
    cv::OutputArray dst
);

OpenCv中的直方图均衡化操作实际并没有用到直方图，仅仅将原始图像与结果图像在直方图上直观展示时用到了直方图操作。

---

OpenCv提供一种数据类型来表达直方图，这个数据类型可以表达一维至多维的直方图，并包括必要的数据以支持均匀或非均匀的组宽，并配备各种有用的函数方便对直方图进行各种操作。

OpenCv中直方图的表示

在C++ API中，OpenCv使用数组表示直方图，可以使用cv::Mat或vector<>或稀疏矩阵cv::SparseMat表示。

当把一个数组视为直方图时，这个数据和普通数据的含义完全不同。

如果一个n维数组被视为直方图，那么数组中的每个元素表示该n维直方图对应组的计数结果，直方图中组的编号即数组某维与该组对应的元素的下标，下标通常是整数。

直方图中组的实际含义不同于该组的编号，当使用直方图时，可能需要在组的实际含义和组的编号之间转换。比如，有一个表达人群体重的直方图，其中的组可能被设计为$20-40$、$40-60$、$60-80$、$80-100$，单位是$kg$，表示为数组时这些组的编号是$0$、$1$、$2$和$3$。

OpenCv也提供了一些函数完成转换工作。

处理一个高维直方图时，经常会出现直方图中大部分元素都是0的情况，这时可以选择使用cv::SparseMat类表示直方图。

---

从数据创建直方图：cv::calcHist()

OpenCv提供函数cv::calcHist()可以从一个或多个数组中创建直方图。

直方图的维度和输入数组的维度或大小无关，而是取决于输入数组的数量。直方图中的每个维度对应于某个输入数组上的某个通道。

如果不想使用图片的所有通道，选择想使用的通道传入cv::calcHist()函数即可。

cv::calcHist()函数声明：

void calcHist(const Mat* images, int nimages, const int* channels, 
              InputArray mask, OutputArray hist, int dims, 
              const int* histSize, const float** ranges, 
              bool uniform=true, bool accumulate=false);

void calcHist(const Mat* images, int nimages, const int* channels, 
              InputArray mask, SparseMat& hist, int dims, 
              const int* histSize, const float** ranges, 
              bool uniform=true, bool accumulate=false);

void calcHist(InputArrayOfArrays images, const vector<int>& channels,
              InputArray mask, OutputArray hist, 
              const vector<int>& histSize, const vector<float>& ranges,
              bool accumulate=false);

前两种方式是C风格数组，第三种使用 STL vector模板类型的参数；前两种的主要区别是计算结果被保存在稠密数组还是稀疏数组中。

以一个示例说明这些参数。假设有一幅8bit三通道图像images，要求计算该图像的后两个通道的直方图，每个通道的直方图分为32个区间，每个区间的范围是均匀分布的。 示例代码如下：

	int nimages = 1;  // 数组个数
    int channels[] = { 1,2};  // 计算数组images中的1、2通道的直方图，通道从0开始
    int dims = 2;  // 输出的直方图是2维
    const int histSize[] = {32, 32};  // 每一通道的区间个数
    float range[] = {0, 256};  // uniform=true时每一维的区间的上限与下限，
                               // 比如对于1维区间范围是(256-0)/32=8，
                               // 其中第一个区间范围[0, 8),第二个区间范围[8, 16)...直到第20个区间范围[248, 256)
    const float *ranges[] = {range, range};  // 计算2个维度的直方图，所以有4个范围，每个范围都是[0,256)
    bool uniform = true;  // true表示使用规范化的情况
    bool accumulate = false;  // false表示计算结果被累加前，将设置hist为0

函数参数详细说明：

第一个参数是数组数据，images是一个指向C风格数组列表的指针，或者是一个更现代化的InputArrayOfArrays。直方图从images或InputArrayOfArrays中一个或更多数组中计算。images数组的要求：通道数可以不同，大小和数组的数据类型必须相同，数组元素可以是8位整数或32位浮点数。

如果以C风格作为输入，必须同时指定nimages作为images中包含的数组个数。

参数channels控制直方图计算时，哪些通道需要被考虑。channel中的整数表示在计算直方图时，使用输入数据images中的哪些通道。通道按顺序进行序列编号，比如images包含2个大小一致、数据类型相同的三通道数组，那么images[0]的3个通道被编号为$0、1、2$，images[1]的3个通道被编号为$3、4、5$，如果要计算images[0]的前2个通道和images[1]的后2个通道，那么channels={0,1,4,5};。channels中的元素个数是计算得到的直方图的维度。

数组mask是一个可选掩膜，可以用来选择images的每个数组中哪些像素参与直方图的计算。mask必须是一个8-bit数组并且和images中的输入数组大小相同。计算直方图时会考虑每个在mask中有非零值的像素，如果不想使用掩膜，传入cv::noArray()。

参数hist是直方图计算的输出值。

参数dims是输出直方图的维度，该值是channels中元素的个数，每个维度的来源由channels指定。

参数histSize表示直方图中每个维度需要分为多少个区间，histSize中元素的个数也应该等于dims，与channels中元素的个数保持一致。

参数ranges指定每个区间对应的值。如果以C风格传参，ranges中的每个元素是一个数组，元素个数等于dims，与参数channel和histSize中元素个数保持一致，这时ranges[i]表示第i维中区间的结构。

参数uniform决定了ranges参数的具体内容。

对于C风格数组

• 如果uniform=true，表示规范化的情况，即第i维中的所有区间都等长，此时只需要指定[下限，上限)，此时得到的是均匀直方图；
• 如果uniform=false，表示非规范化的情况，即第i维中的区间值需从ranges[i]中获取， 此时得到的是非均匀直方图。

对于vector风格的数组，含义与使用C风格时相同，只是将C风格中的内容摊平成为一维数组

• 规范化情况下，按照维度的顺序每个维度对应两个元素；
• 非规范化情况下按照维度的顺序每个维度对应$N+1$个元素。

简单说，在均匀直方图中，只需提供每个区间的最小边界和最大边界，在非均匀直方图中，需要提供每一维度中的每个区间的最小边界和最大边界。

参数accumulate表示在从images得到的数据被累加进入hist之前，不要将其中的元素删除，重新分配或是设置为0。

---

显示直方图

calcHist()计算得到的直方图hist不能直接显示出来，需要经过处理绘制直方图。

// 绘制二维直方图
void Draw2DimsHistogram(const cv::InputArray &calchist, const int *histSize, int scale, const char* histname = "histogram")
{
    cv::Mat hist_img(histSize[0]*scale, histSize[1]*scale, CV_8UC3);
    cv::Mat hist = calchist.getMat();
    for(int h=0; h<histSize[0]; ++h){
        for(int w=0; w<histSize[1]; ++w){
            float hVal = hist.at<float>(h,w);
            cv::rectangle(hist_img, cv::Rect(h*scale,w*scale, scale, scale), cv::Scalar::all(hVal), -1);
        }
    }

    cv::imshow(histname, hist_img);
}
// 绘制一维直方图
void Draw1DimHistogram(const cv::InputArray &calchist, const int histSize, int scale, const char *histname = "historgam")
{
    // 获取最大值
    double maxVal;
    cv::minMaxIdx(calchist, NULL, &maxVal);

    cv::Mat hist_img(maxVal + 20, histSize*scale, CV_8UC3);
    cv::Mat hist = calchist.getMat().t();

    for(int w=0; w<histSize; ++w){
        float hVal = hist.at<float>(0,w);
        cv::rectangle(hist_img, cv::Rect(w*scale, hist_img.rows-hVal, scale, int(hVal)), cv::Scalar(0,0,hVal), -1);
    }

    cv::imshow(histname, hist_img);
}
// 绘制一维直方图的折线图
void Draw1DimLineChartm(const cv::InputArray &calchist, const int histSize, int scale, const char *histname = "Line chart")
{
    // 获取最大值
    double maxVal;
    cv::minMaxIdx(calchist, NULL, &maxVal);

    cv::Mat hist_img(maxVal + 20, histSize*scale, CV_8UC3);

    cv::Mat hist = calchist.getMat().t();

    for(int w=1; w<histSize; ++w){
        float preVal = hist.at<float>(0, w-1);
        float hVal = hist.at<float>(0,w);
        cv::line(hist_img, cv::Point((w-1)*scale, hist_img.rows - preVal), cv::Point(w*scale, hist_img.rows - hVal), cv::Scalar(0,0,255), 2, 8);
    }

    cv::imshow(histname, hist_img);
}

---

直方图归一化

构造直方图时，首先需要将信息放入在各个区间。有时希望将直方图变为归一化的形式，这时的每个区间表示的是该区间内的信息占总体的百分比。比如说，对一幅8bit灰度图来说，设定区间为灰度值$[0,255]$， 那么归一化前每个区间表示图像中当前灰度级的像素数量，归一化后表示当前灰度级的像素数量占总像素数量的百分比。

在C++ API中，可以简单使用数组的代数算子和操作完成直方图的归一化，如下：

cv::Mat normalized = my_hist / sum(my_hist)[0];
// 或者
cv::normalize(my_hist, my_hist, 1, 0, NORM_L1);

---

直方图二值化

如果希望将直方图二值化并丢弃所有其中元素个数少于给定值的区间，可以使用标准数组二值化函数：

cv::threshold(my_hist, my_threshold_hist, threshold, 0, cv::THRESHOLD_TOZERO);

---

找出最显著的区间

如果希望找出所有元素个数高于某个给定阈值的区间，或者希望找出有最多元素的区间，比如在使用直方图表示概率分布的情况时，可以选择使用cv::minMaxLoc()。

函数声明如下：

void minMaxLoc( cv::InputArray src, 
				double *minVal, double *maxVal, 
				cv::Point* minLoc=0, cv::Point* maxLoc=0,
				cv::InputArray mask = cv::noArray);

void minMaxLoc(const cv::SparseMat& src, 
				double* minVal, double* maxVal, 
				int* minLoc=0, int* maxLoc=0);

该函数需要传入minVal和maxVal用来存放计算出来的最小值和最大值，需要传入minLoc和maxLoc存放计算出的最小值和最大值的位置。如果不想要某个计算结果，将该参数置为NULL即可。

当处理二维数组时，可以使用cv::InputArray的形式。

当处理二维直方图时，可以使用cv::SparseMat的形式。如果处理的是一个一维vector<>数组，可以使用cv::Mat(vec).reshape(1)将其转换为一个$N\times 1$的二维数组。

需要注意使用稀疏矩阵作为输入时，要求传入的minLoc和maxLoc为int*型，这是因为稀疏矩阵形式的minMaxLoc()支持任意维的矩阵，因此需要手动分配存放位置的变量并确保其可存放n维稀疏直方图对应的原图中的一个点。

---

比较两个直方图

可以通过对两幅图像取直方图，并通过直方图比较方法来比较原来的两幅图像，也可以借助直方图比较方法在图像中识别物体，方法是将物体的直方图和图片中不同的子区域的直方图进行比较，通过直方图相配的程度来判断该子区域是否有物体。

OpenCv提供函数cv::compareHist()通过特殊的判据对两个直方图的相似度进行度量。

cv::compareHist()函数声明：

double cv::compareHist(cv::InputArray H1, cv::InputArray H2, int method);
double cv::compareHist(const cv::SparseMat& H1, const cv::SparseMat& H2, int method);

前两个参数是待比较的直方图，该直方图应该具有相同的大小。

第三个参数是需要选择的距离度量方法。OpenCv提供四个可用的方法：

• 相关性方法cv::COMP_CORRL，使用基于统计相关性的方法，实现了皮尔逊相关性系数方法，计算公式：$d_{correl}(H_1, H_2) = \frac{ {\textstyle \sum_{i}^{} H_1’(i) \cdot H_2’(i) } } {\sqrt{ {\textstyle \sum_{i}^{} H_1’^2(i) \cdot H_2’^2(i) } } } $，这里的$H_1$和$H_2$解释为概率分布。大的相关性系数比小的相关性系数匹配的好。完全匹配的相关性系数为$1$， 完全不匹配的相关性系数为$-1$， $0$表示两个分布没有关系，随机组合；
• 卡方方法cv::COMP_CHISQR_ALT，该距离度量是基于卡方检验统计量，是一种检验两个分布是否相关的替换检验方法，计算公式：$d_{chi-square} (H_1, H_2) = \sum_{i}^{} \frac{ (H_1(i) - H_2(i))^2 } { H_1(i) + H_2(i) } $，对于该检验方法，低分值表示直方图匹配的很好，完全匹配的分值为$0$，完全不匹配的分值无下限，依赖于直方图的大小；
• 交集法cv::COMP_INTERSECT，简单基于两个直方图的交集，该方法对两个直方图中的共同部分求和，计算公式：$d_{intersection}(H_1,H_2)={\sum }_i^{}min(H_1(i),H_2(i))$，对于该检验方法，高分值表示匹配的好，如果两个直方图都进行了归一化，$1$表示完全匹配，$0$表示完全不匹配。
• 巴氏距离cv::COMP_BHATTACHARYYA，对两个分布重叠程度的一种度量方法，计算公式：$d(H_1, H_2) = \sqrt{1- \frac{ {\textstyle \sum_{i}^{} H_1(i) \cdot H_2(i)} }{\sqrt{ {\textstyle \sum_{i}^{} H_1(i) \cdot {\textstyle \sum_{i}^{} H_2(i)} } } } } $，对于该检验方法，值越小表示匹配的效果越好，$0$表示完全匹配，$1$表示完全不匹配。

交集法在快速而粗略的匹配中效果很好，卡方法和巴氏距离法效果更好，但是速度更慢。另外还有EMD距离方法可以比较直方图，该方法最符合直觉的匹配效果，但是计算速度更慢。

---

四、OpenCv提供的一些复杂的直方图操作

OpenCv提供的一些可用的复杂的方法，在某些特定应用中比较有用。

---

EMD距离

EMD距离的基本思路是：通过将一部分(或全部)直方图搬到一个新位置，度量花多大的功夫才能把一个直方图搬到另一个直方图里。

光照的变化会使得颜色值产生很大的偏移，这种偏移不改变颜色直方图的形状，上面介绍的相关性法、卡方方法、交集法、巴氏距离法都是对直方图颜色位置的度量，而对直方图颜色位置的移动度量不准确。EMD距离是一种对平移不敏感的距离度量方法。EMD距离可以在任意维度下工作。

EMD算法允许用户设置自己的距离度量或是自己的移动花费矩阵，即记下材料如何从一个直方图流向另一个直方图的，并用从数据的先验信息导出的非线性距离对其度量。OpenCv提供的EMD函数为cv::EMD()，函数声明如下：

float cv::EMD(cv::InputArray signature1, cv::InputArray signature2, 
              int distType, cv::InputArray cost = cv::noArray(), 
              float* lowerBound = 0, 
              cv::OutputArray flow = cv::noArray());

这个函数要求使用签名的方式传入前两个数组参数，签名要求是float类型的数组，每行包括直方图区间的计数值，接下来是该区间的坐标。比如对于下列的一维直方图，其签名分别为：上-$[[1,0],[0,1]]$；中-$[[0.5,0],[0.5,1]]$；下-$[[0,0],[1,1]]$。如果在一个三维直方图$(x,y,z)$位置上有区间计数$537$，那么该区间这个位置的签名为$[537,x,y,z]$。在调用cv::EMD()函数之前需要将直方图转换为签名的形式。

参数distType应该选择以下之一：

• 曼哈顿距离cv::DIST_L1
• 欧几里得距离cv::DIST_L2
• 棋盘距离cv::DIST_C
• 用户自定义距离cv::DIST_USER，使用该选择时需要通过参数cost传进一个预先计算好的矩阵，这个矩阵大小是一个$n_1\times n_2$，其中$n_1$和$n_2$是signature1和signature2的大小。

参数lowerBound有两个功能，一个作为输入，一个作为输出。作为输出时，表示两个直方图重心距离的下限，要计算这个下限，必须提供一个标准的距离度量方法，同时两个签名的总权重必须相同，比如直方图归一化后的情况。如果选择提供一个下限，必须将该值初始化为一个有意义的值，低于这个下限的，EMD距离才会被计算。如果希望任何情况下都计算EMD距离，将lowerBound置为0即可。

参数flow是一个可选的$n_1\times n_2$的矩阵，用来记录从signature1的第$i$个点流向signature2的第$j$个点的质量，本质上给出的是计算整个EMD中质量的具体安排情况。

示例：从直方图为EMD算法构造签名，在不同的光照条件下对手部的直方图进行比较。代码运行工具：Qt。

void on_action_EMD_triggered()
{
    QStringList files;
    // 0.jpg：model图片（该图片会被拆分为上下两部分） 1.jpg：和第一张图片一样 2.jpg/3.jpg/4.jpg：与第一张图片进行比较的三张图片
    files << "0.jpg" << "1.jpg" << "2.jpg" << "3.jpg" << "4.jpg";

    std::vector<cv::Mat> src(5);
    cv::Mat tmp;
    // 读取model图片
    tmp = cv::imread(files.at(0).toStdString().data());
    if(tmp.empty()){
        qCritical() << "Error on reading image 1," << files.at(0) << "\n\n";
        return;
    }
    // 将第一张图片拆分一半
    cv::Size size = tmp.size();
    int width = size.width;
    int height = size.height;
    int halfheight = height >> 1;

    qDebug() << "Getting size [[" << tmp.cols << "] [" << tmp.rows << "]]\n\n";
    qDebug() << "Got size (w, h): (" << width << ", " << height << ")\n";

    src[0] = cv::Mat(cv::Size(width, halfheight), CV_8UC3);
    src[1] = cv::Mat(cv::Size(width, halfheight), CV_8UC3);

    // 将第一张图像分为上下两部分，分别赋给src[0]和src[1]
    cv::Mat_<cv::Vec3b>::iterator tmpit = tmp.begin<cv::Vec3b>();
    // 上半部分
    cv::Mat_<cv::Vec3b>::iterator s0it = src[0].begin<cv::Vec3b>();
    for(int i=0; i<width*halfheight; ++i, ++tmpit, ++s0it)
        *s0it = *tmpit;
    // 下半部分
    cv::Mat_<cv::Vec3b>::iterator s1it = src[1].begin<cv::Vec3b>();
    for(int i=0; i<width*halfheight; ++i, ++tmpit, ++s1it)
        *s1it = *tmpit;

    // 加载另外三张图像
    for(int i=2; i<5;++i){
        src[i] = cv::imread(files.at(i).toStdString().data());
        if(src[i].empty()){
            qCritical() << "Error on reading image " << i << ": " << files.at(i) << "\n";
            return;
        }
    }

    // 计算HSV图像，分解为单独的平面
    std::vector<cv::Mat> hsv(5), hist(5), hist_img(5);
    int h_bins = 8;
    int s_bins = 8;
    int hist_size[] = {h_bins, s_bins}, ch[] = {0,1};
    float h_range[] = {0, 180};
    float s_range[] = {0, 360};
    const float *range[] = {h_range, s_range};
    int scale = 30;

    // 计算并绘制直方图
    for(int i=0; i<5; ++i){
        // 转换为HSV图像
        cv::cvtColor(src[i], hsv[i], cv::COLOR_BGR2HSV);
        //  计算直方图
        cv::calcHist(&src[i], 1, ch, cv::noArray(), hist[i], 2, hist_size, range);
        // 归一化
        cv::normalize(hist[i], hist[i], 0, 255, cv::NORM_MINMAX);

        // 绘制直方图
        hist_img[i] = cv::Mat::zeros(hist_size[0]*scale, hist_size[1]*scale, CV_8UC3);

        for(int h=0; h<hist_size[0]; ++h){
            for(int s=0; s<hist_size[1]; ++s){
                float hval = hist[i].at<float>(h,s);
                cv::rectangle(hist_img[i],
                              cv::Rect(h*scale, s*scale, scale, scale),
                              cv::Scalar::all(hval), -1);
            }
        }

    }

    // 显示
    int index=0;
    cv::namedWindow("0source", cv::WINDOW_AUTOSIZE); cv::imshow("0source", hsv[index]);
    cv::namedWindow("0H-S Histogram", cv::WINDOW_AUTOSIZE); cv::imshow("0H-S Histogram", hist_img[index++]);

    cv::namedWindow("1source", cv::WINDOW_AUTOSIZE); cv::imshow("1source", hsv[index]);
    cv::namedWindow("1H-S Histogram", cv::WINDOW_AUTOSIZE); cv::imshow("1H-S Histogram", hist_img[index++]);

    cv::namedWindow("2source", cv::WINDOW_AUTOSIZE); cv::imshow("2source", hsv[index]);
    cv::namedWindow("2H-S Histogram", cv::WINDOW_AUTOSIZE); cv::imshow("2H-S Histogram", hist_img[index++]);

    cv::namedWindow("3source", cv::WINDOW_AUTOSIZE); cv::imshow("3source", hsv[index]);
    cv::namedWindow("3H-S Histogram", cv::WINDOW_AUTOSIZE); cv::imshow("3H-S Histogram", hist_img[index++]);

    cv::namedWindow("4source", cv::WINDOW_AUTOSIZE); cv::imshow("4source", hsv[index]);
    cv::namedWindow("4H-S Histogram", cv::WINDOW_AUTOSIZE); cv::imshow("4H-S Histogram", hist_img[index++]);

    // 比较直方图 src0 vc src1 , vs src2, vs src3, vs src4
    std::cout << "Comparsion:\n"
             << "\t\t  Corr    Chi    Intersect   Bhat\n";

    for(int i=1; i<5; ++i){
        std::cout << "Hist[0] vs Hist[" << i << "]: ";
        for(int j=0;j<4;j++){  // 4种算法
            std::cout << /*"method[" << j << "]: "  <<*/ cv::compareHist(hist[0], hist[i], j) << "  ";
        }
        std::cout << std::endl;
    }

    // 使用EMD方法比较并输出数据
    std::vector<cv::Mat> sig(5);
    std::cout << "\nEMD:" << std::endl;

    // 转换为签名形式
    for(int i=0; i<5;++i){

        std::vector<cv::Vec3f> sigv;

        // 归一化直方图使得总和为1
        cv::normalize(hist[i], hist[i], 1, 0, cv::NORM_L1);
        // 转换
        for(int h=0; h<h_bins; ++h){
            for(int s=0; s<s_bins; ++s){
                float bin_val = hist[i].at<float>(h,s);
                if(bin_val != 0){
                    sigv.push_back(cv::Vec3f(bin_val, float(h), float(s)));
                }
            }
        }

        // 转换为 Nx3 32FC1的矩阵，n是直方图区间的个数
        sig[i] = cv::Mat(sigv).clone().reshape(1);

        if(i > 0){
            std::cout << "Hist[0] vs Hist[" << i << "]:"
                      << cv::EMD(sig[0], sig[i], CV_DIST_L2) << std::endl;
        }

    }

}

---

反向投影

反向投影是计算像素和直方图模型中像素吻合度的一种方法。比如，现有肤色的直方图，可以使用反向投影在图像中寻找肤色区域。

OpenCv提供实现这种基础操作的函数：cv::calcBackProject()，该函数从输入图像的指定通道中计算出一个向量。不同于cv::calcHist()在直方图中记录累计值，反向投影从输入图像的直方图中读取当前像素对应的计数值作为结果。比如，计算输入图像的H-S直方图，在某个区间的计数概率为$p$，那么就将当前图像中在该区间的所有像素置为$p$。

从统计学的角度来看，如果将输入的直方图视为某个物体上特定的向量的一个概率分布，那么反向投影就是计算图片上某个特定部分来自该先验分布的概率。

函数声明如下：

void cv::calcBackProject(const cv::Mat* images, int nimages, 
                         const int* channels, 
                         cv::InputArray hist, cv::OutputArray backProject, 
                         const float** ranges, double scale, 
                         bool uniform = true);

void cv::calcBackProject(const cv::Mat* images, int nimages,
                        const int* channels,
                        const cv::SparseMat& hist,
                         cv::OutputArray backProject,
                        const float** ranges, double scale = 1,
                        bool uniform = true);

void cv::calcBackProject(cv::InputArrayOfArrays images,
                        const vector<int>& channels,
                        cv::InputArray hist,
                        cv::OutputArray backProject,
                        const vector<float>& ranges,
                        double scale = 1,
                        bool uniform = true);

cv::calcBackProject()函数以单通道或是多通道数据集合的形式提供图像，即传入的images参数。同时以cv::calcHist()输出的直方图的格式传入直方图，即hist参数。如果使用C风格数组，需要参数nimages指定输入数组中元素的个数。

参数channels指定在反向投影中发挥作用的通道的列表，该参数与cv::calcHist()时的参数形式一致。

反向投影的计算结果保存在参数backProject中，该参数和images[0]的大小类型相同，只有一个通道。

参数ranges作用与cv::calcHist中的参数作用一致。

参数scale是一个可选的应用于backProject的缩放因子，如果希望对结果可视化，这个参数很有用。

参数uniform表示输入的直方图是不是一个均匀的直方图，和cv::calcHist中意义相同。

在新的图片中寻找一个物体或是需要的区域的一个方法如下：

1. 创建要寻找的物体或区域的直方图；
2. 为了在新图片中找到它，使用步骤1中的直方图对新图片进行cv::calcBackProject()以创建一个反向投影图，在反向投影图中，具有最大值的区域很可能包含感兴趣的物体；
3. 反向投影中的高值区域取局部直方图并使用cv::compareHist()将它与要寻找的物体或区域的直方图进行比较；

---

模板匹配

OpenCv提供函数cv::matchTemplate()进行模板匹配，但是该函数实现原理不基于直方图，而是使用一个图像块在输入图像上进行滑动，并用指定的匹配方法进行比较。

cv::matchTemplate()函数声明：

void cv::matchTemplate(cv::InputArray image,
                      cv::InputArray temp1,
                      cv::OutputArray result,
                      int method);

参数image是一幅8bit或浮点型灰度或彩色图像。

参数temp1是一个包含给定物体的另一张图片上选取的模板图片块，另一张图片和当前图片相似。

参数result存放计算结果，是一个单通道、大小为image.width - temp1.width +1, image.height - temp1.height +1、以整数字节或浮点型存储的图片。

参数method表示匹配方法，每一种匹配方法，都有一个归一化的版本。归一化的方法可以降低模板和图片之间由于光照不同引起的效果。具体方法如下所示，$I$表示输入图像，$T$表示模板，$R$表示输出的结果图像。

• 方差匹配方法cv::TM_SQDIFF，以方差为依据进行匹配，完全匹配结果为0， 不匹配会得到一个很大的值。计算公式：$R_{sq\_diff}={\sum }_{x^{\prime },y^{\prime }}^{}[T(x^{\prime },y^{\prime })-I(x+x^{\prime },y+y^{\prime }){]}^2$。

• 归一化方差匹配方法cv::TM_SQDIFF_NORMED，是方差匹配方法的归一化版本，完全匹配结果为0。计算公式：$R_{sq_diff_normed} = \frac{ \sum_{x’, y’}^{} [T(x’, y’) - I(x+x’, y+y’)]^2 }{\sqrt{ \sum_{x’, y’}^{} T(x’, y’)^2 \cdot \sum_{x’, y’}^{} I(x+x’, y+y’)^2 } } $。

• 相关性匹配方法cv::TM_CCORR，以相乘的方式进行模板匹配，完全匹配结果值很大，不匹配会得到一个很小的值或0。计算公式：$R_{ccorr}={\sum }_{x^{\prime },y^{\prime }}^{}T(x^{\prime },y^{\prime })\cdot I(x+x^{\prime },y+y^{\prime })$。

• 归一化的互相关匹配方法cv::TM_CCORR_NORMED，是相关性匹配方法的归一化版本，图片和模板极度不匹配，结果为0。计算公式：$R_{ccorr_normed} = \frac{R_{ccorr} = \sum_{x’, y’}^{} T(x’, y’) \cdot I(x+x’, y+y’)}{\sqrt{\sum_{x’, y’} T(x’, y’)^2} \cdot \sum _{x’, y’} I(x+x’, y+y’)^2 } $。

• 相关系数匹配方法cv::TM_CCOEFF，该方法以模板相对于其平均值的变化和图片相对于其平均值的变化进行匹配，完全匹配会得到1，完全不匹配得到-1， 如果是随机图片匹配得到0。计算公式：

$$\begin{gathered} R_{ccoeff}=\sum _{x^{\prime },y^{\prime }}{T}^{\prime }(x^{\prime },y^{\prime })\cdot I^{\prime }(x+x^{\prime },y+y^{\prime }) \\ {T}^{\prime }(x^{\prime },y^{\prime })=T(x^{\prime },y^{\prime })-\frac{{\sum }_{x^{\prime \prime },y^{\prime \prime }}T(x^{\prime \prime },y^{\prime \prime })}{w-h} \\ {I}^{\prime }(x+x^{\prime },y+y^{\prime })=I(x+x^{\prime },y+y^{\prime })-\frac{{\sum }_{x^{\prime \prime },y^{\prime \prime }}I(x^{\prime \prime },y^{\prime \prime })}{w-h} \end{gathered}$$

• 归一化的相关系数匹配方法cv::TM_CCOEFF_NORMED，相关系数匹配方法的归一化版本，相对好的匹配得到正值，误匹配得到负值。计算公式：$R_{ccoedd\_normed}=\frac{{\sum }_{x^{\prime },y^{\prime }}{T}^{\prime }(x^{\prime },y^{\prime })\cdot I^{\prime }(x+x^{\prime },y+y^{\prime })}{\sqrt{{\sum }_{x^{\prime },y^{\prime }}{T}^{\prime }(x^{\prime },y^{\prime }{)}^2\cdot {\sum }_{x^{\prime },y^{\prime }}{I}^{\prime }(x+x^{\prime },y+y^{\prime }{)}^2}}$，其中$T^{\prime }$和$I^{\prime }$与相关系数匹配中含义一致。

实际使用中可以从一个相对简单的度量方法换成一个更复杂的度量方法，比如从方差换成相关系数，会得到更精确的结果，但同时计算时间也会更长。最好的办法是尝试所有的度量方法，选择一个可以兼顾精确度和计算时间的最好的方法。

---

五、 MATLAB中的直方图操作

MATLAB提供了一些直方图操作函数。

计算并显示图像直方图

首先imread函数读取图像，然后imhist函数计算图像直方图，最后使用图窗绘制函数subplot及图像显示函数imshow将原图及结果显示出来。具体参考代码如下：

MATLAB版本：R2014B

%% 显示图像直方图

filename = './images/lena.jpg';
img = imread(filename);

% 如果是彩色图，转换为灰度图
if ndims(img) < 3
  grayimg = img;
else
    grayimg = rgb2gray(img);
end

% 显示原图
subplot(2,2,1); imshow(img); title('原图');
subplot(2,2,2); imshow(grayimg); title('灰度图');
% 计算并显示直方图，传入的图像为灰度图
subplot(2,2,[3,4]); bar(imhist(grayimg, 256), 'b');title('图像直方图');

直方图归一化

利用imhist()得到图像直方图，将该直方图除以像素总数即得到归一化的直方图。

MATLAB版本：R2014B

%% 图像直方图归一化

filename = './images/lena.jpg';
img = imread(filename);

% 如果是彩色图，转换为灰度图
if ndims(img) < 3
  grayimg = img;
else
    grayimg = rgb2gray(img);
end

% 显示原图
subplot(2,2,1); imshow(img); title('原图');
subplot(2,2,2); imshow(grayimg); title('灰度图');
% 计算并显示直方图，传入的图像为灰度图，默认划分256个灰度级，可以设置该参数
h = imhist(grayimg, 256);  % 计算图像直方图
subplot(2,2,3); bar(h, 'b'); title('图像直方图');
subplot(2,2,4); bar(h/numel(grayimg), 'r'); title('图像直方图归一化');

直方图均衡化

histeq函数实现图像直方图均衡化。

MATLAB版本：R2014B

%% 直方图均衡化

filename = './images/lena.jpg';
img = imread(filename);

% 如果是彩色图，转换为灰度图
if ndims(img) < 3
  grayimg = img;
else
    grayimg = rgb2gray(img);
end

% 显示原图
subplot(2,2,1); imshow(grayimg); title('原始灰度图');
% 计算并显示直方图，传入的图像为灰度图，默认划分256个灰度级，可以设置该参数
h1 = imhist(grayimg, 256);  % 计算图像直方图
subplot(2,2,3); bar(h1, 'b'); title('原始灰度直方图');
e = histeq(grayimg);  % 直方图均衡化
h2 = imhist(e);  % 计算均衡化后图像的直方图
subplot(2,2,2); imshow(e); title('均衡化后的图像');
subplot(2,2,4); bar(h2, 'b'); title('均衡化后图像的灰度直方图');

正比例变换

加入一幅图像的灰度范围在$[40,200]$之间，将其缩放到$[0,255]$范围。

MATLAB版本：R2014B

%% 正比例变换
clc;
filename = './images/lena.jpg';
img = imread(filename);
if ndims(img) < 3
  grayimg = img;
else
    grayimg = rgb2gray(img);
end

subplot(2,2,1); imshow(grayimg); title('(a)原始灰度图');
subplot(2,2,2); imhist(grayimg); title('(b)原始灰度图的统计直方图')
l = min(min(grayimg))
h = max(max(grayimg))
% 原始图像灰度值最大为20， 最小为245，将其缩放到[0, 255]
a = imadjust(grayimg, [20/255, 245/255], [0, 1]);
subplot(2,2,3); imshow(a); title('(c)变换图像');
subplot(2,2,4); imhist(a); title('(d)变换图像的灰度统计直方图')