C++笔记之Eigen库的使用
code review!
文章目录
- C++笔记之Eigen库的使用
- 0.矩阵构造和矩阵初始化
- 1.声明一个2\*3的float矩阵:Matrix<float, 2, 3> matrix_23;
- 2.初始化Matrix<float, 2, 3> matrix_23;
- - 使用逗号初始化器:
- - 使用赋值运算符逐个赋值:
- 3.声明一个3维向量Vector3d
- - Vector3d v_3d;
- - Matrix<double, 3, 1> vd_3d;
- 4.初始化Vector3d
- 5.初始化Matrix<float, 3, 1> vd_3d
- 6.将3维向量或矩阵初始化为零
- 7.将向量或矩阵初始化为零
- 8.动态大小的二维矩阵
- 9.矩阵和向量元素访问
- 10.矩阵和矩阵相乘
- 11.矩阵和向量相乘
- 12.eigen中的成员函数colwise()
- 13.矩阵相乘前的类型转换
- 14.矩阵转置
- 15.矩阵四则运算中的加减
- 16.矩阵除以标量(矩阵的数乘)
- 17.矩阵乘以标量(矩阵的数乘)
- 18.矩阵各元素和
- 19.矩阵的迹
- 20.矩阵的逆
- 21.矩阵除法(实际上是矩阵与逆矩阵的乘法)
- 23.矩阵的行列式
- 24.矩阵的特征值和特征向量
- 25.使用Eigen库中的SelfAdjointEigenSolver类来计算一个3x3矩阵的特征值和特征向量
- 26.解线性方程组 Ax = b,使用LU分解
- 27.解线性方程组 Ax = b,使用QR分解
- 27.解线性方程组 Ax = b,使用Cholesky分解
- 28.将旋转向量转为旋转矩阵
- 29.将旋转矩阵转为旋转向量
- 30.使用旋转向量对向量进行旋转的坐标变换
- 31.将旋转矩阵转换为欧拉角
- 32.创建欧氏变换矩阵
- 33.使用变换矩阵进行坐标变换
- 34.创建四元数
- 35.使用四元数旋转向量
- 36.使用刚体变换(欧氏变换)来进行旋转和平移操作
- 37.eigen的数据类型
- 38.eigen的block()函数
- 39.eigen中的.col()和.row()方法
- 40.eigen的点乘和叉乘.dot()和.cross()
- 41.元素乘积.prod()——即向量中所有元素的乘积
- 42.元素均值.mean()
- 43.查找向量或矩阵中的最小值和最大值minCoeff()和maxCoeff()
- 44.生成随机矩阵random()
- 45.用于处理数组(元素级操作)的数据结构Array类
- 46.eigen中Array类的常见操作
0.矩阵构造和矩阵初始化

1.声明一个2*3的float矩阵:Matrix<float, 2, 3> matrix_23;
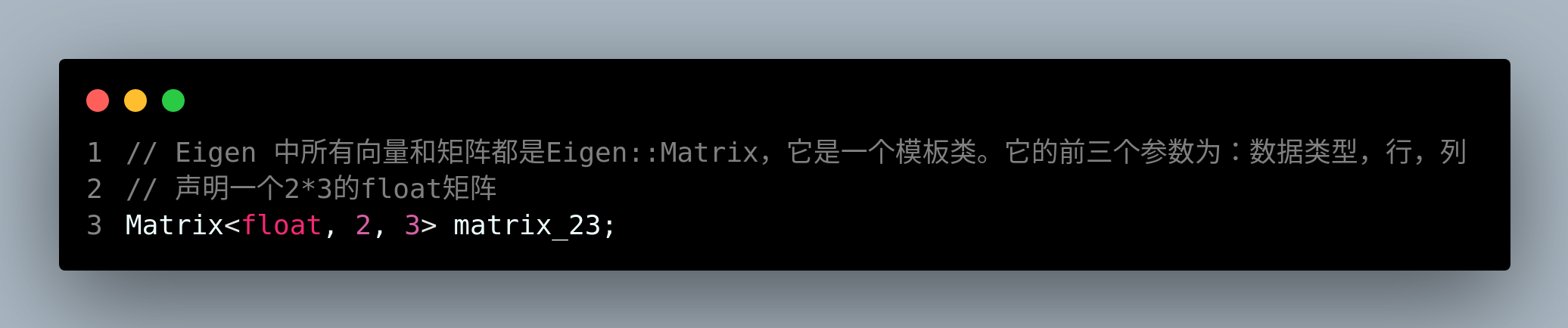
2.初始化Matrix<float, 2, 3> matrix_23;
- 使用逗号初始化器:
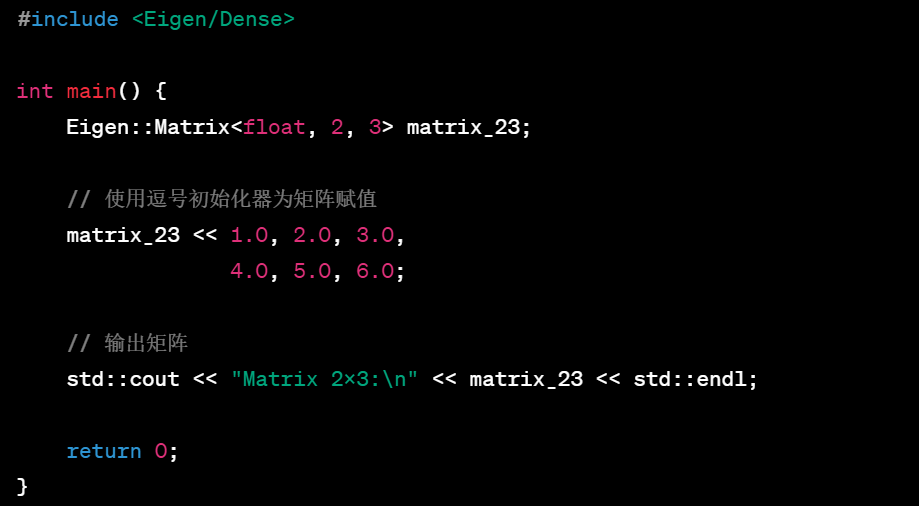
- 使用赋值运算符逐个赋值:
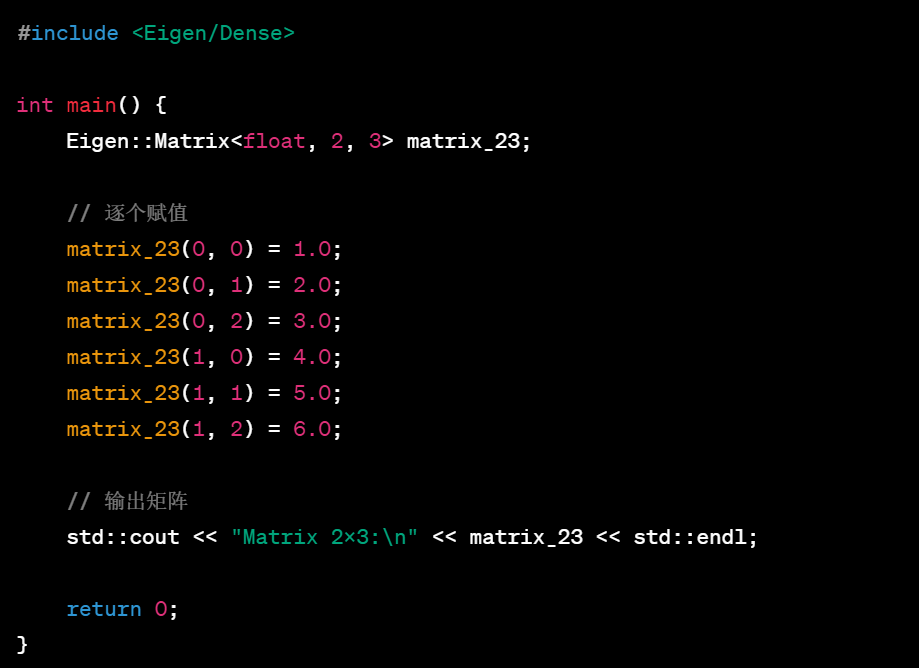
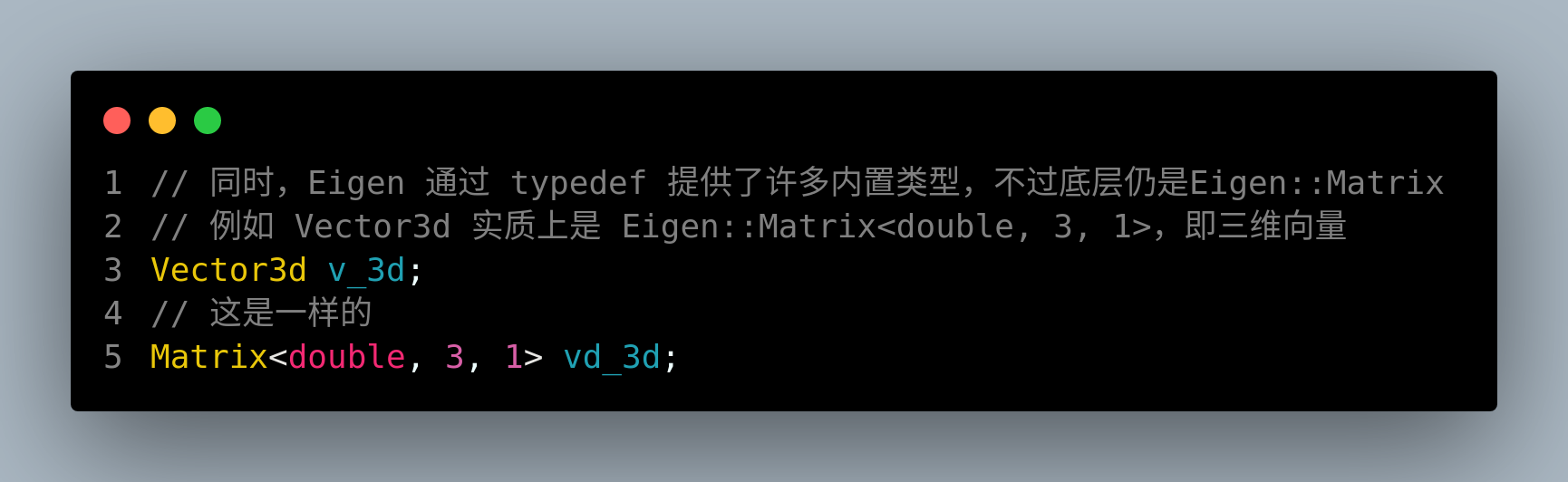
3.声明一个3维向量Vector3d
下述两种方法是等价的
- Vector3d v_3d;
- Matrix<double, 3, 1> vd_3d;
4.初始化Vector3d
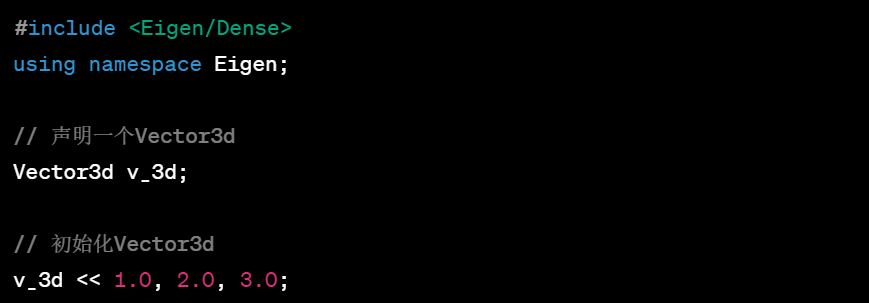
5.初始化Matrix<float, 3, 1> vd_3d

6.将3维向量或矩阵初始化为零
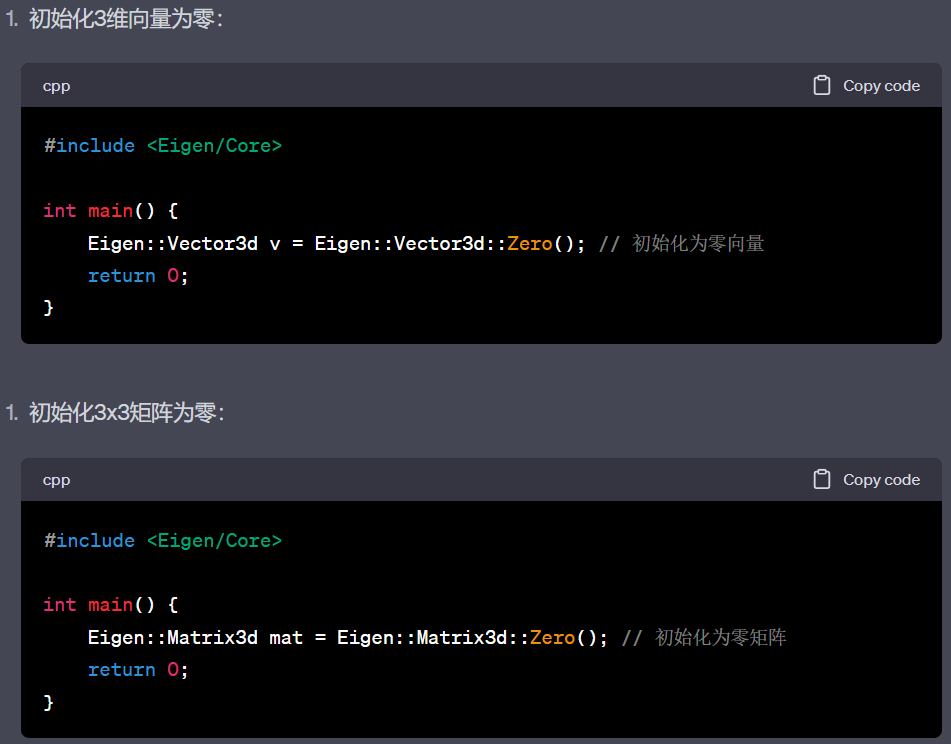
7.将向量或矩阵初始化为零
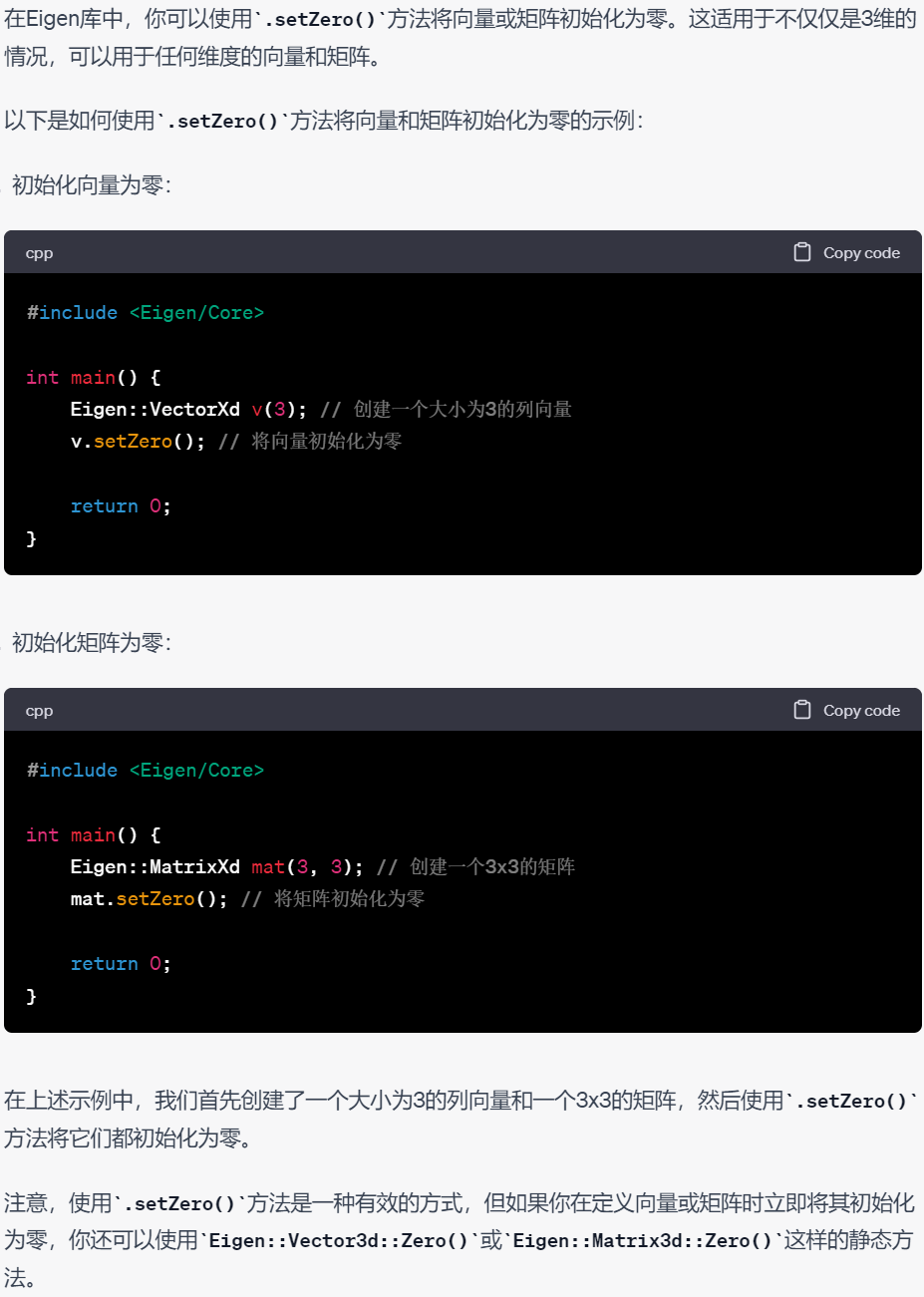
8.动态大小的二维矩阵
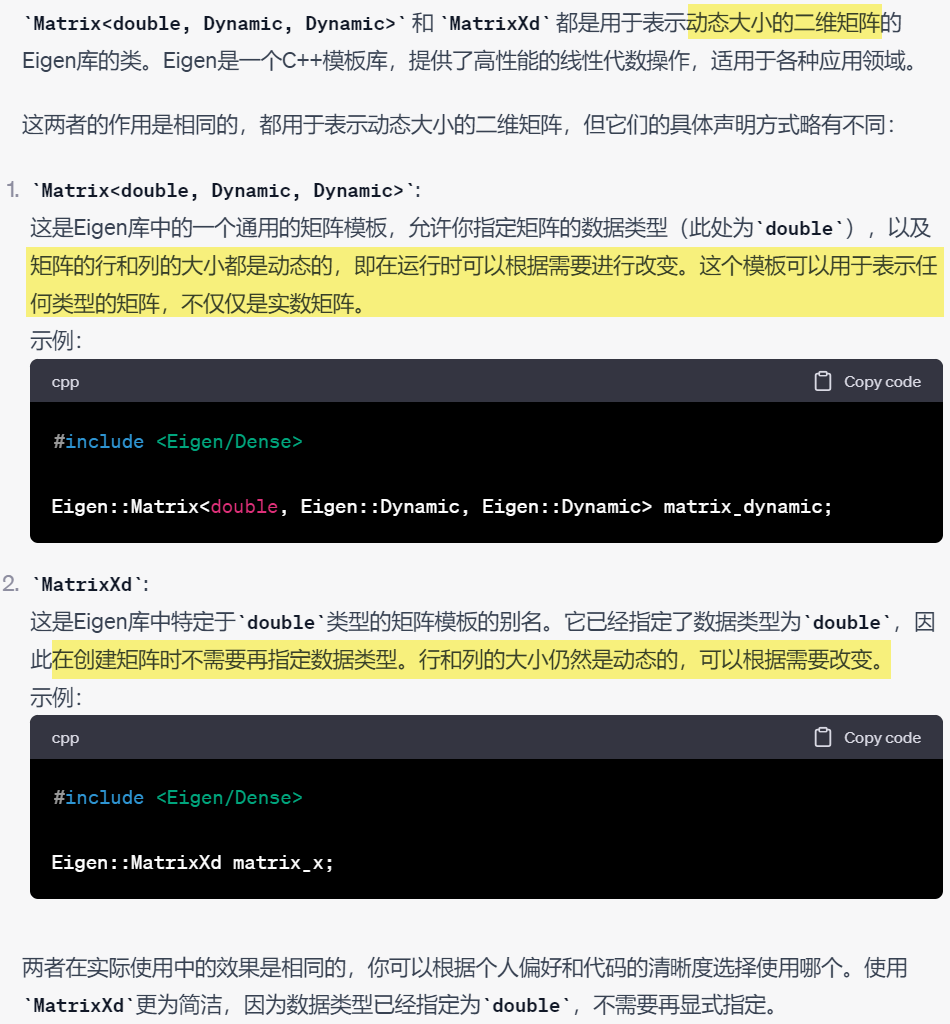
9.矩阵和向量元素访问
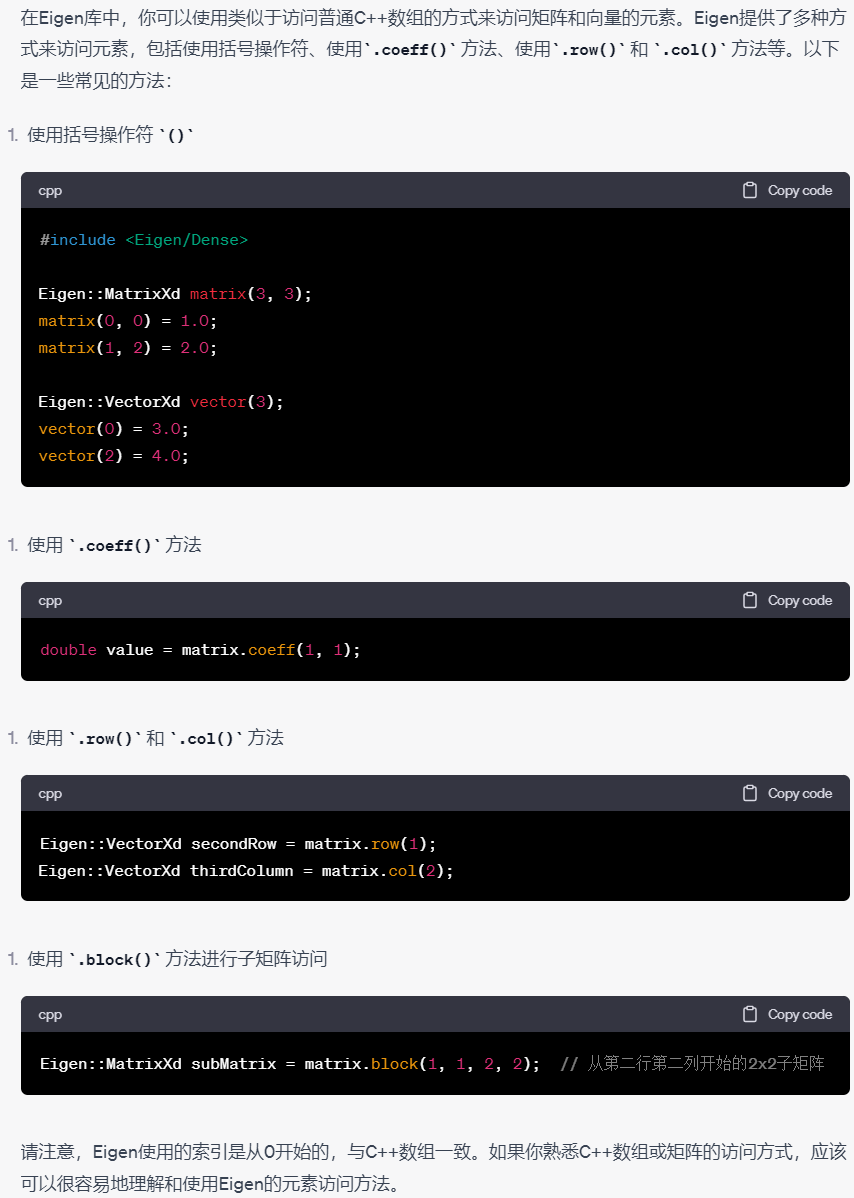
10.矩阵和矩阵相乘
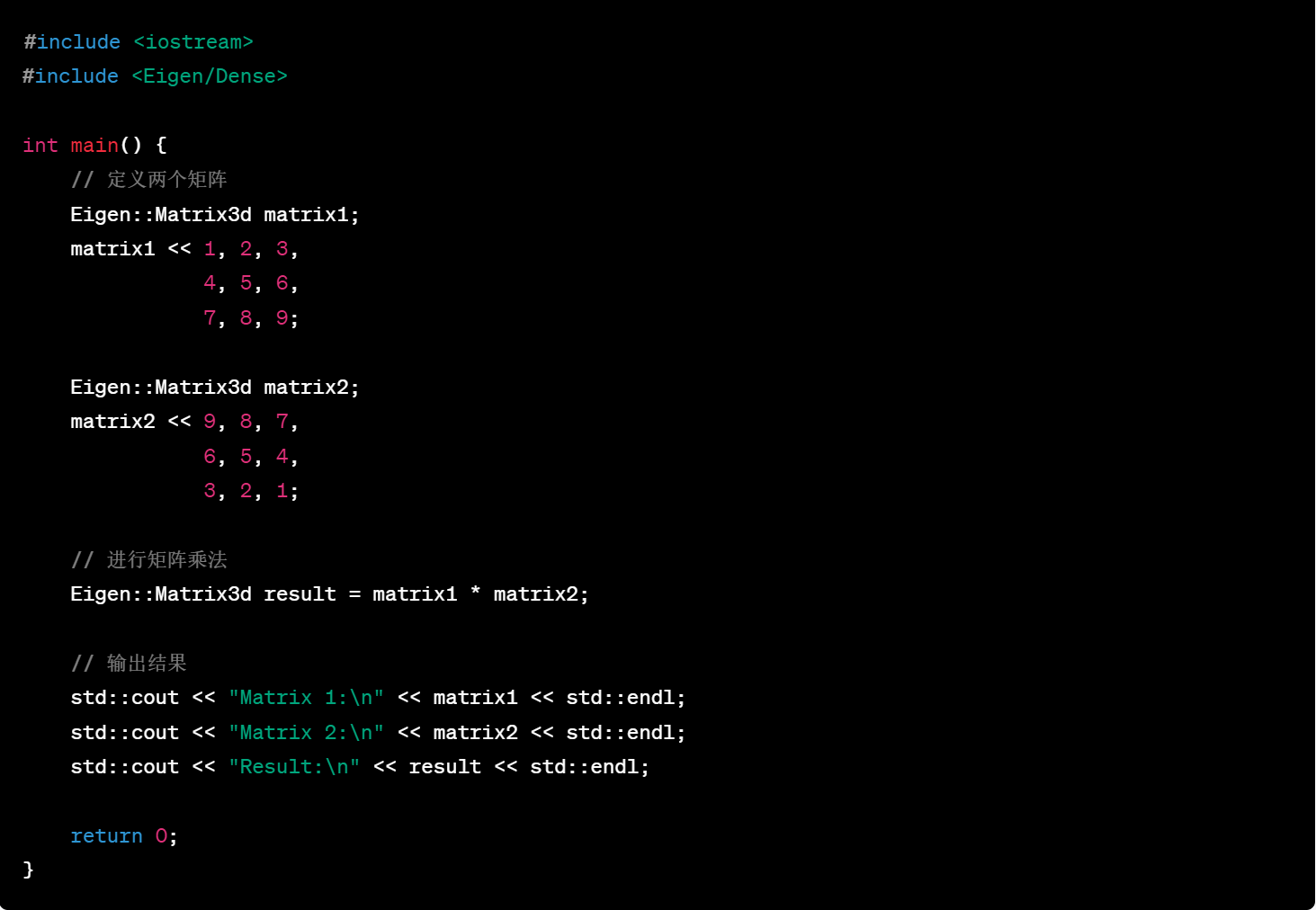
11.矩阵和向量相乘
-
方法一:使用矩阵乘法运算符
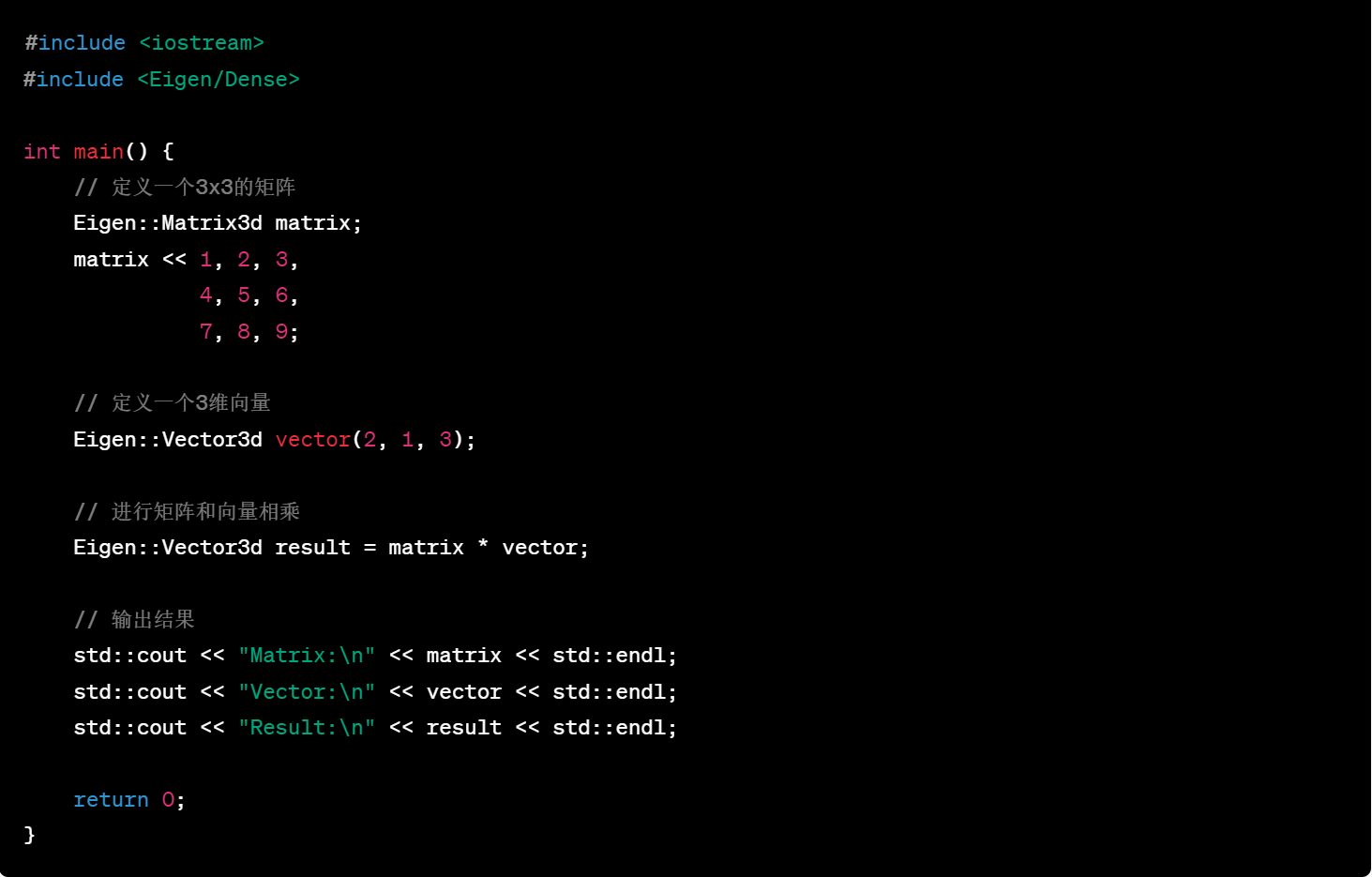
-
方法二:使用矩阵的 dot() 成员函数
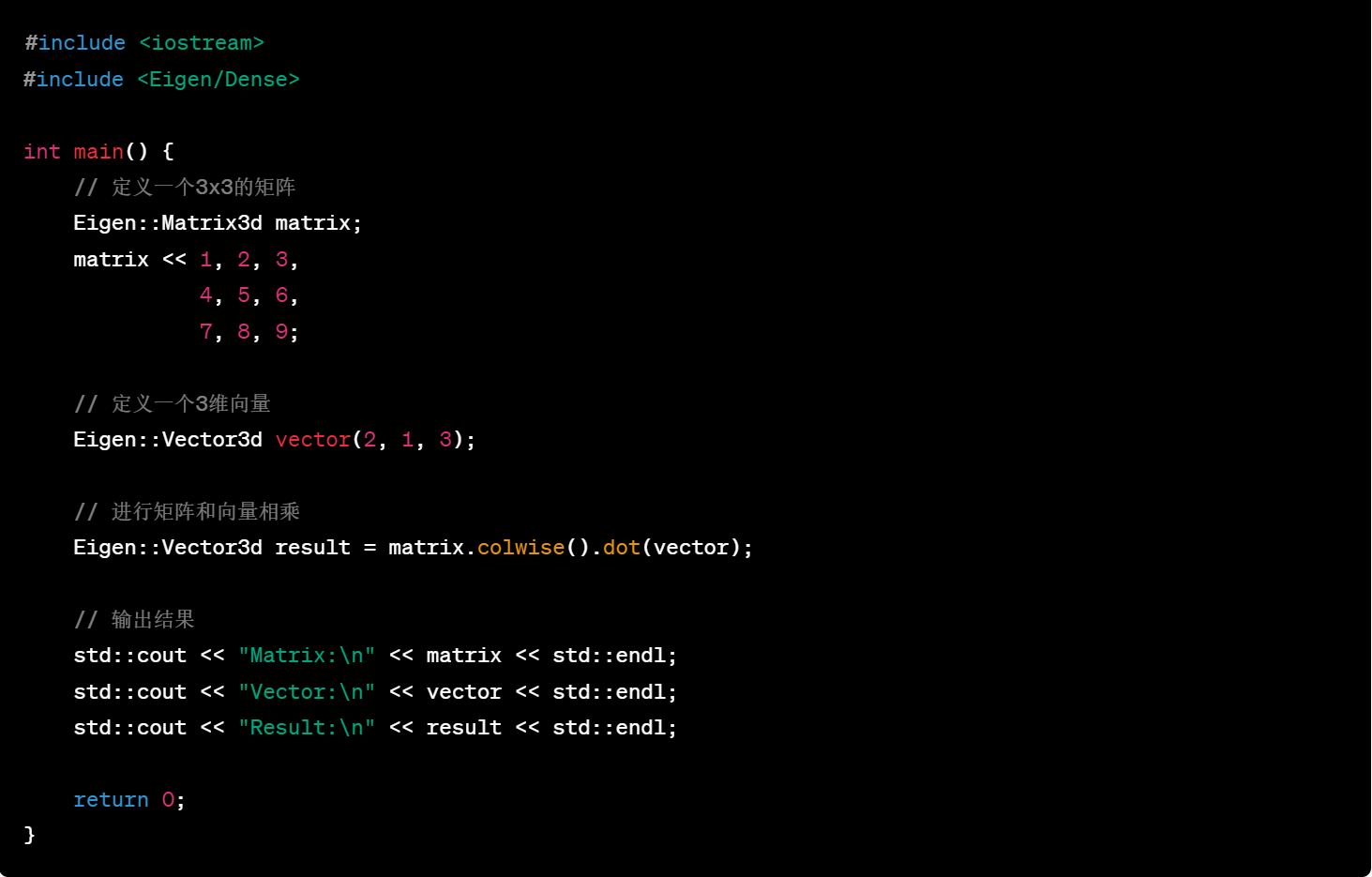
12.eigen中的成员函数colwise()
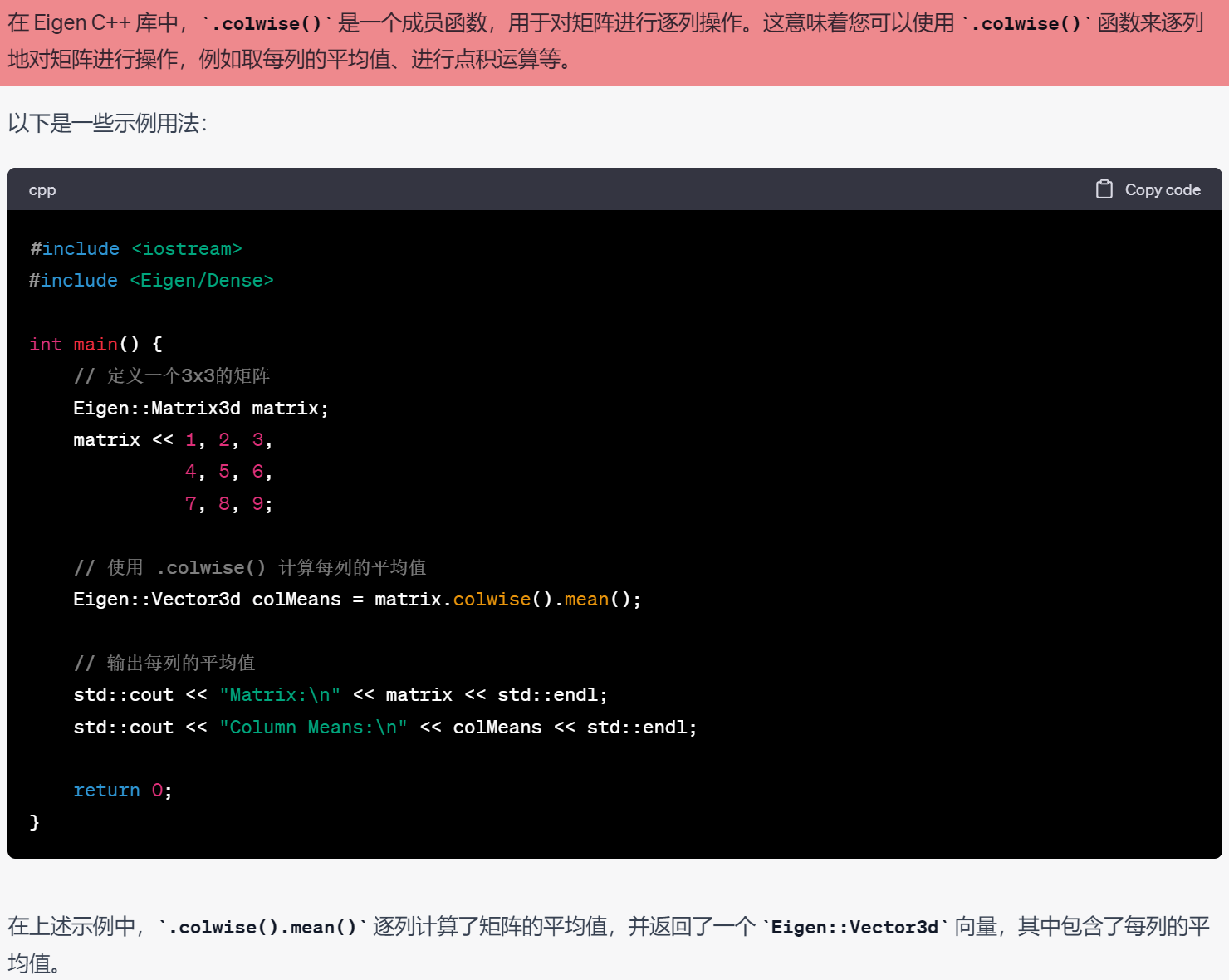
13.矩阵相乘前的类型转换
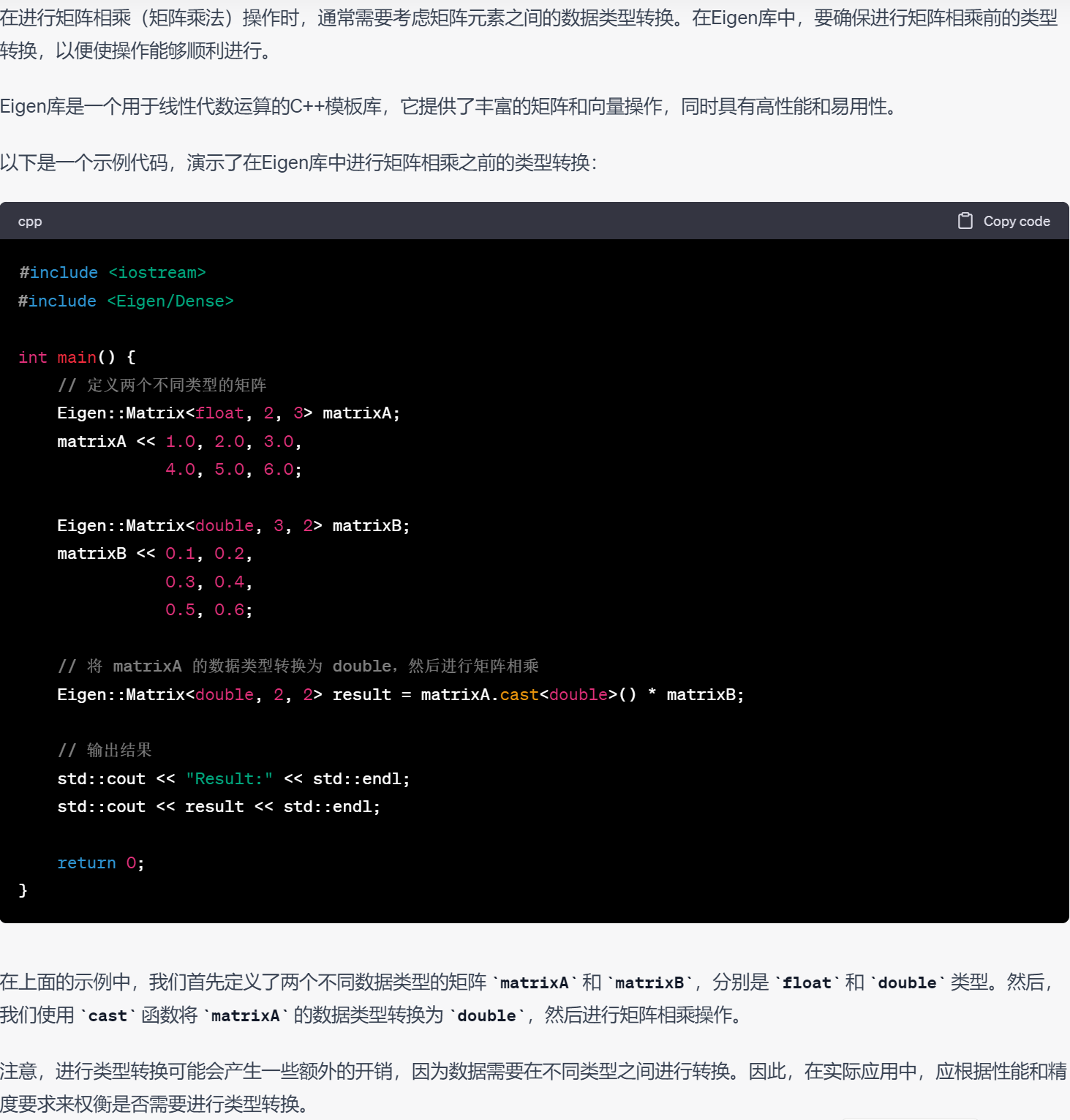
14.矩阵转置
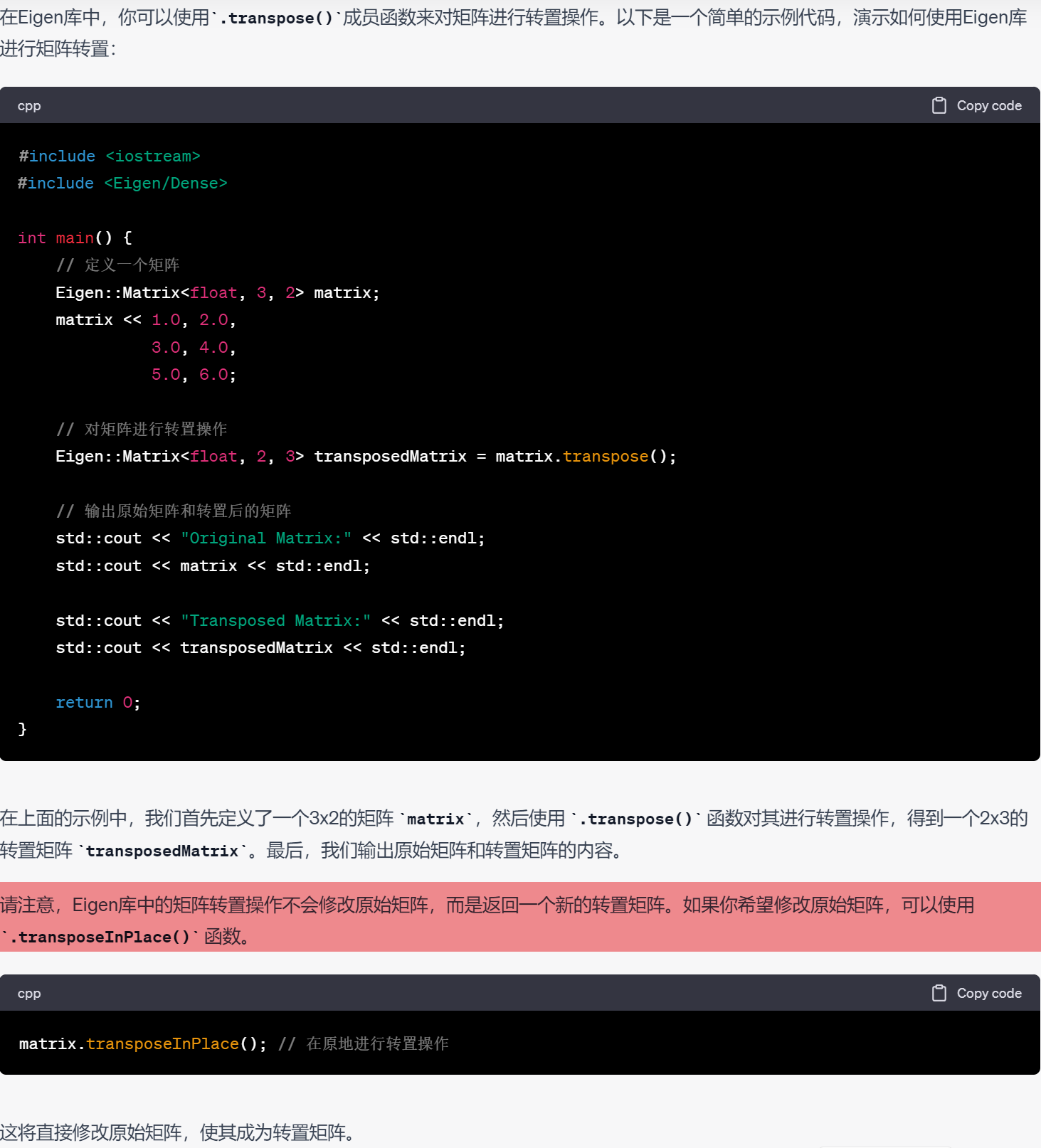
15.矩阵四则运算中的加减
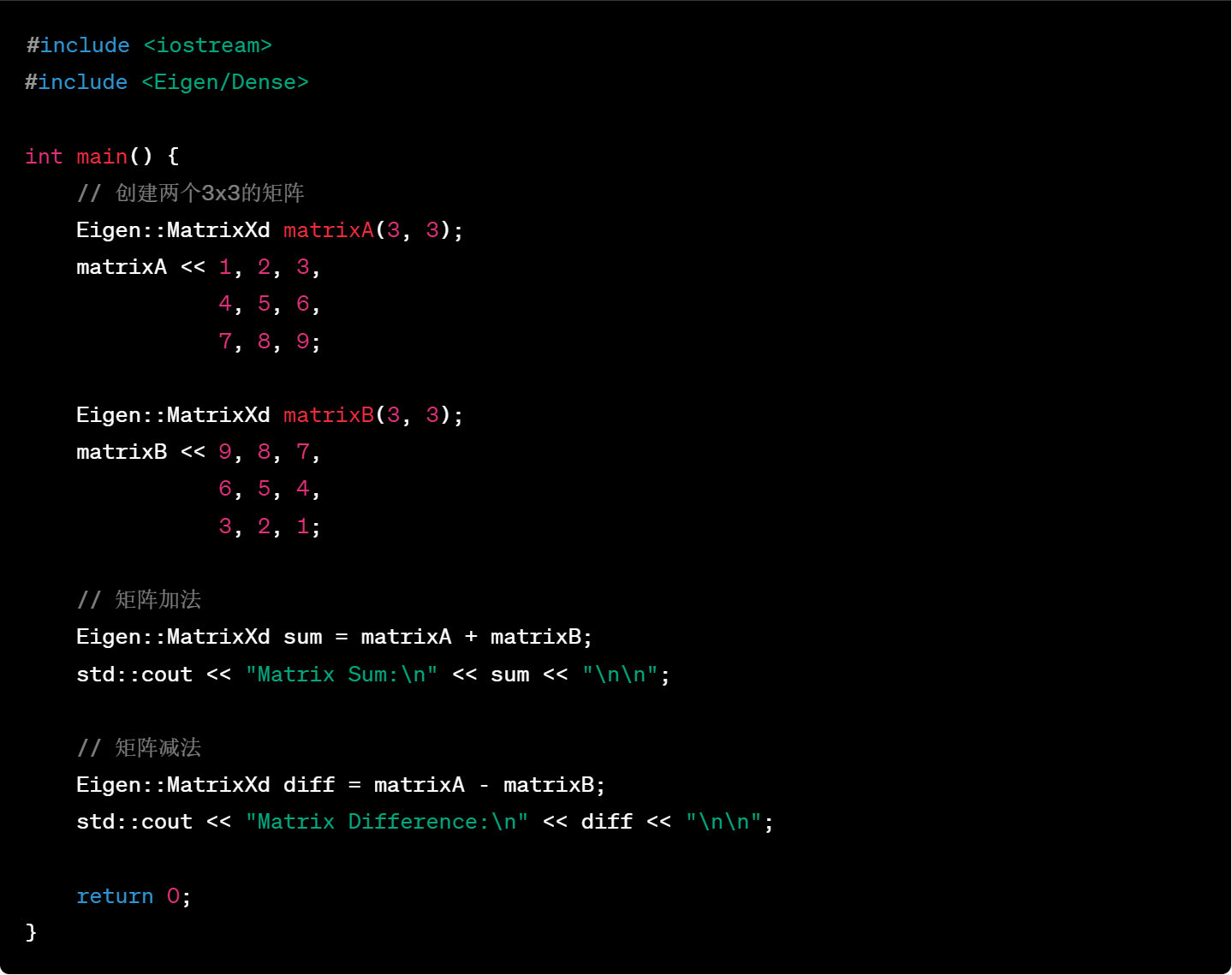
16.矩阵除以标量(矩阵的数乘)

17.矩阵乘以标量(矩阵的数乘)

18.矩阵各元素和
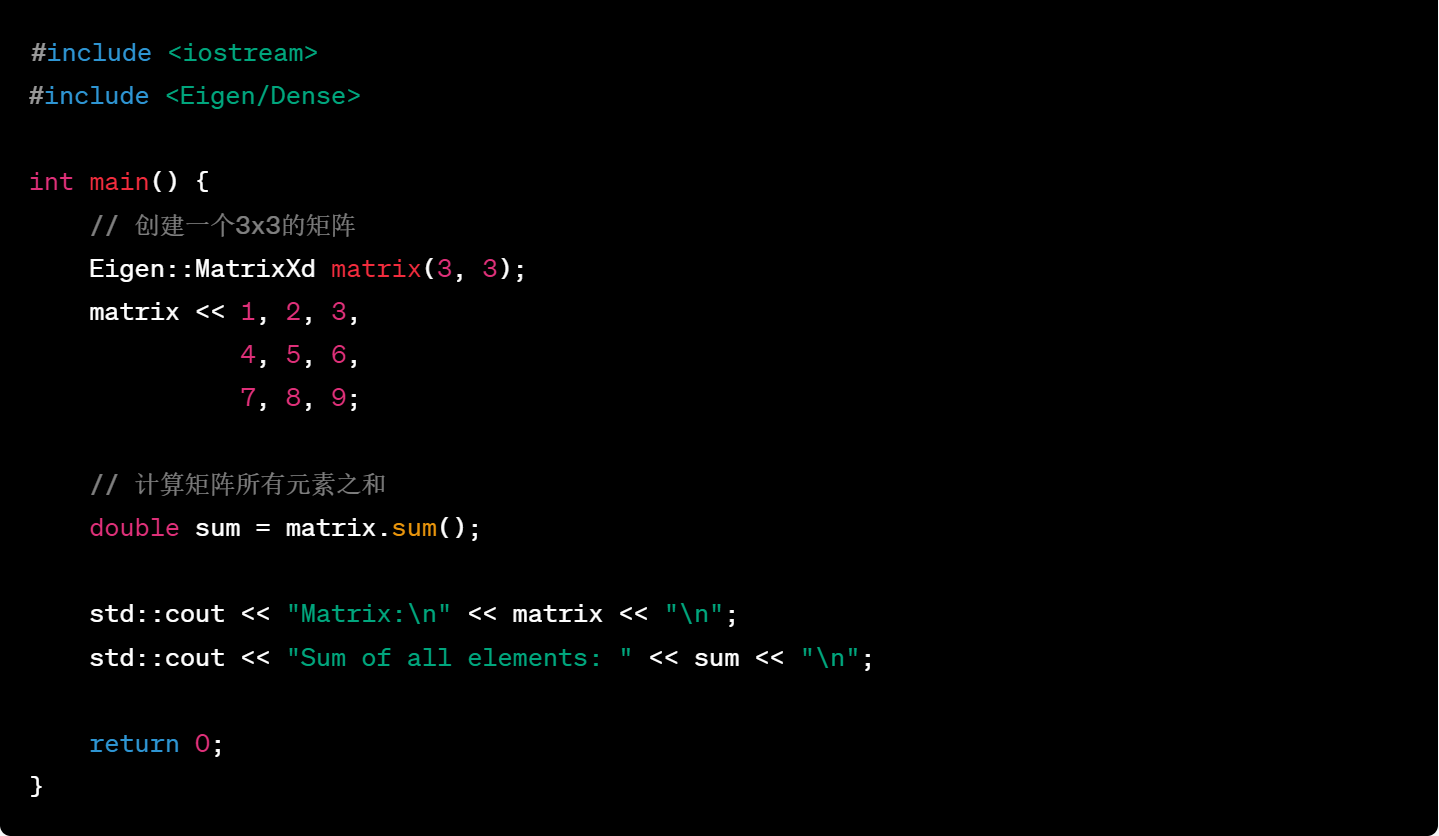
19.矩阵的迹
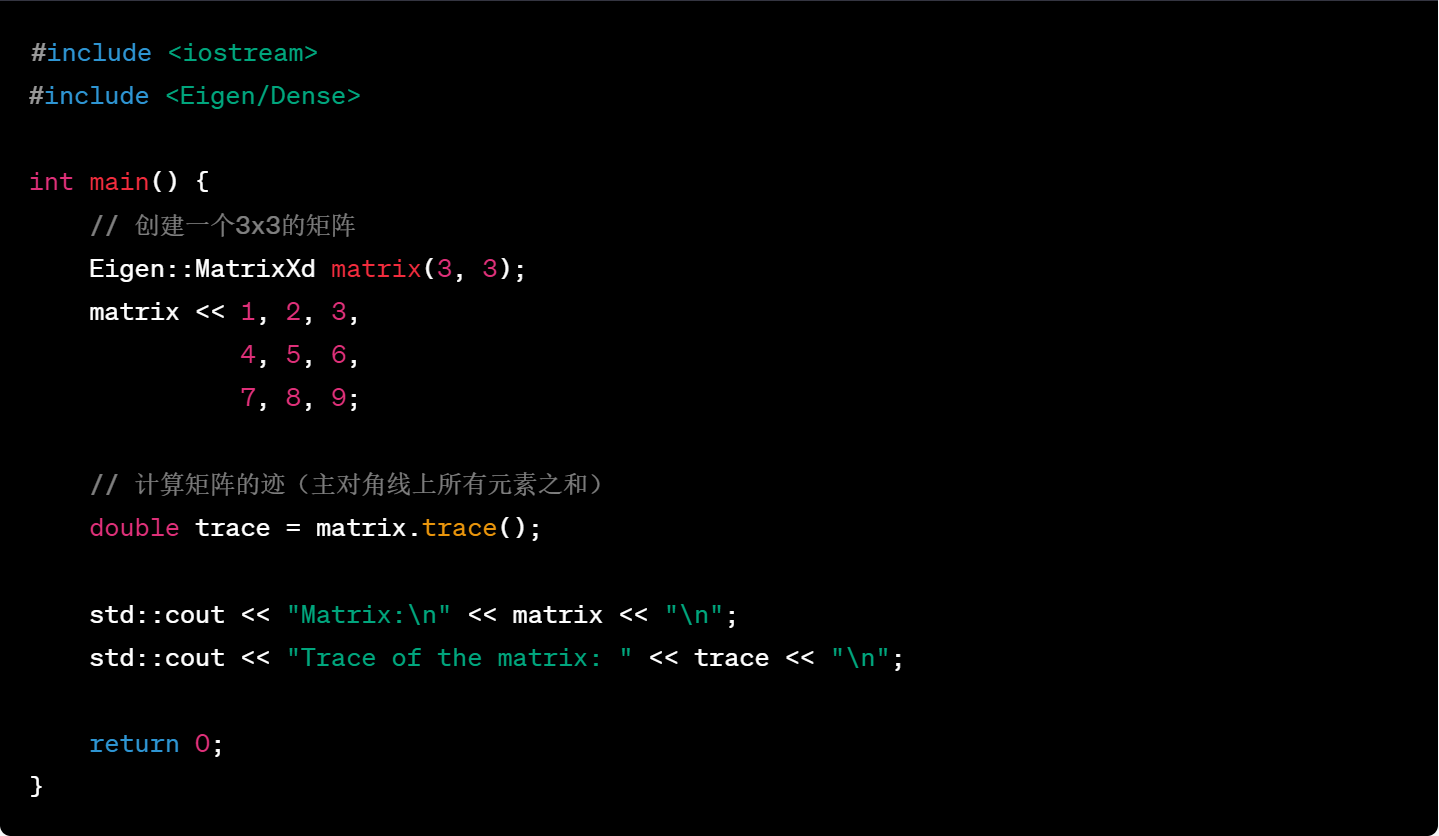
20.矩阵的逆
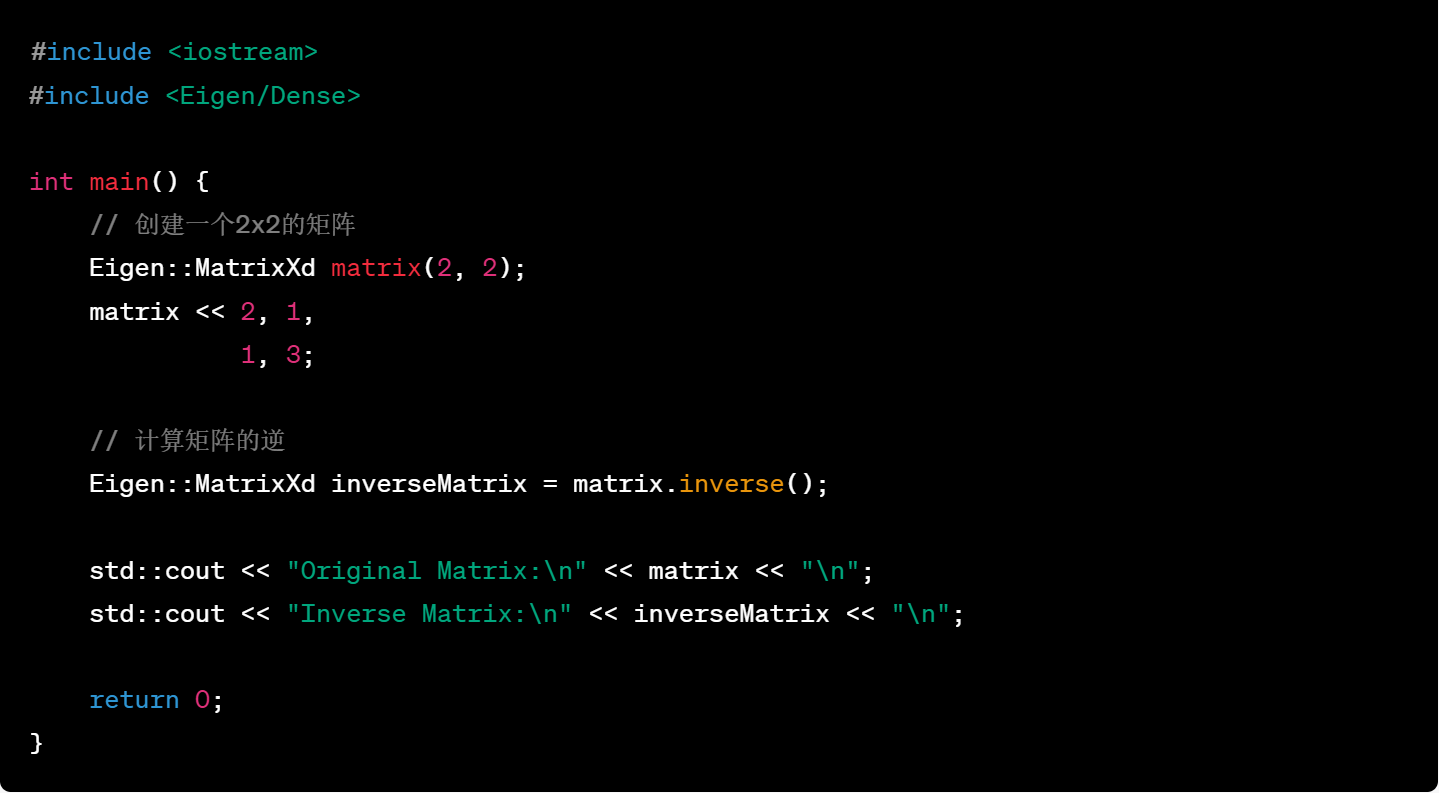
21.矩阵除法(实际上是矩阵与逆矩阵的乘法)
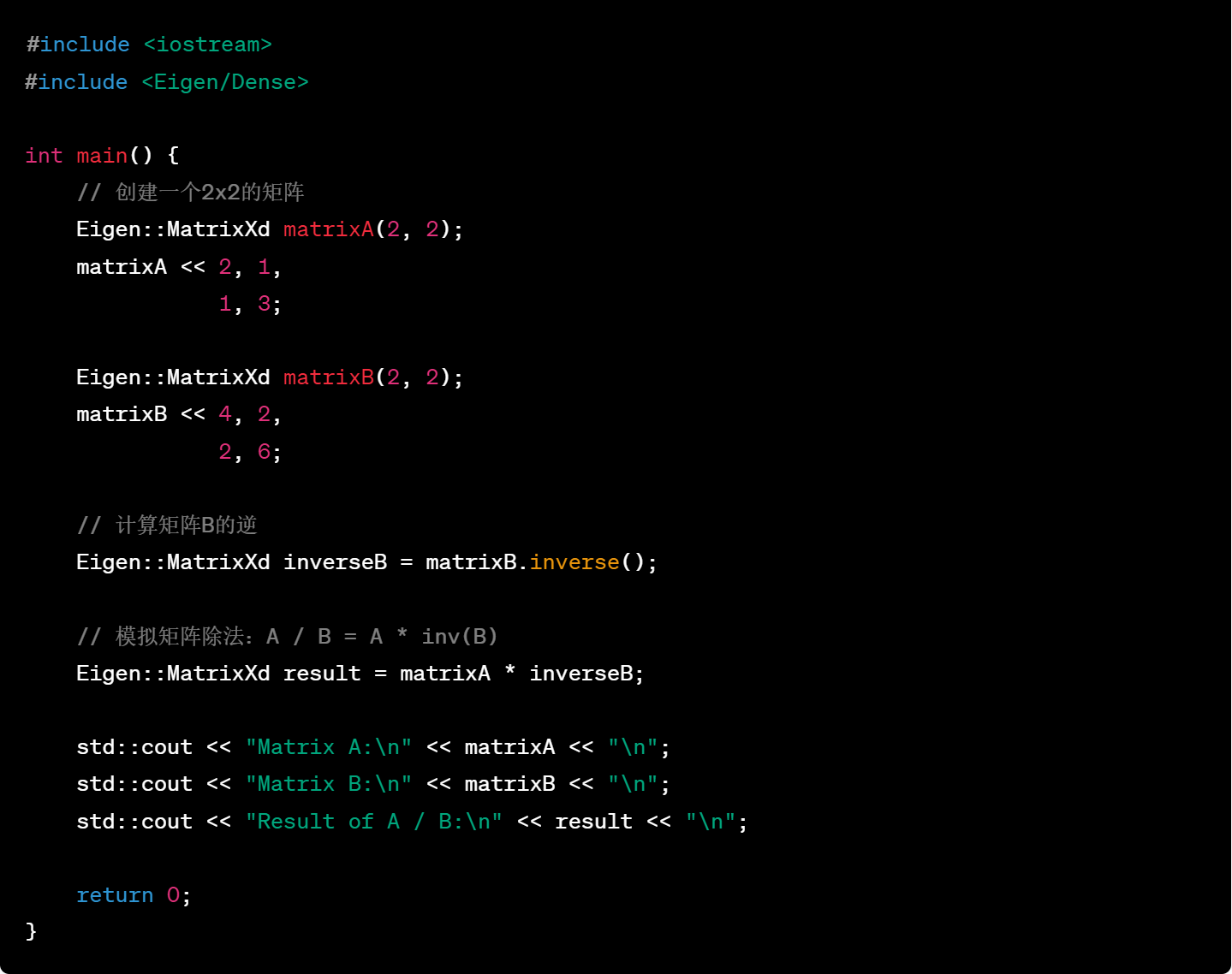
23.矩阵的行列式
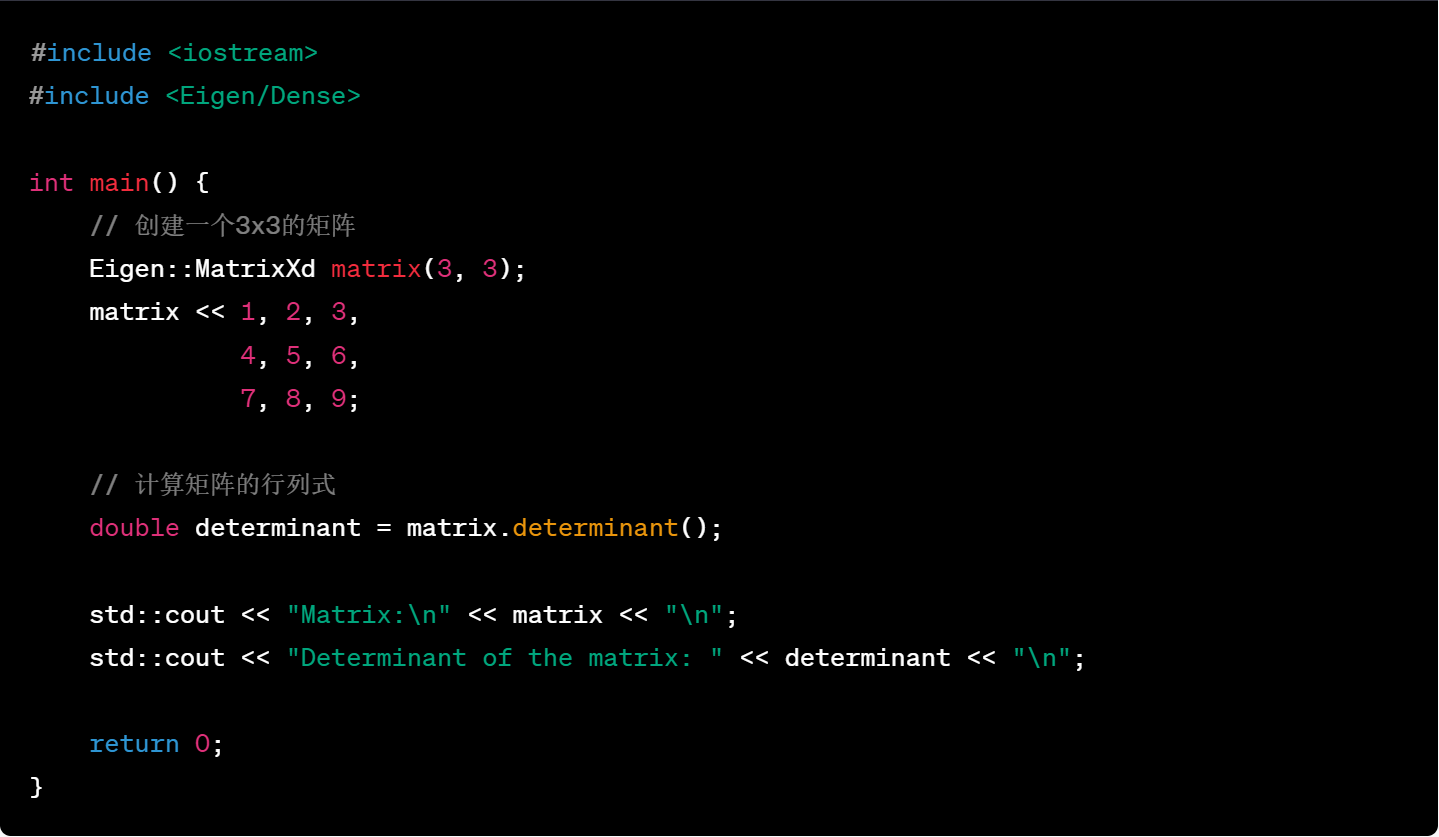
24.矩阵的特征值和特征向量
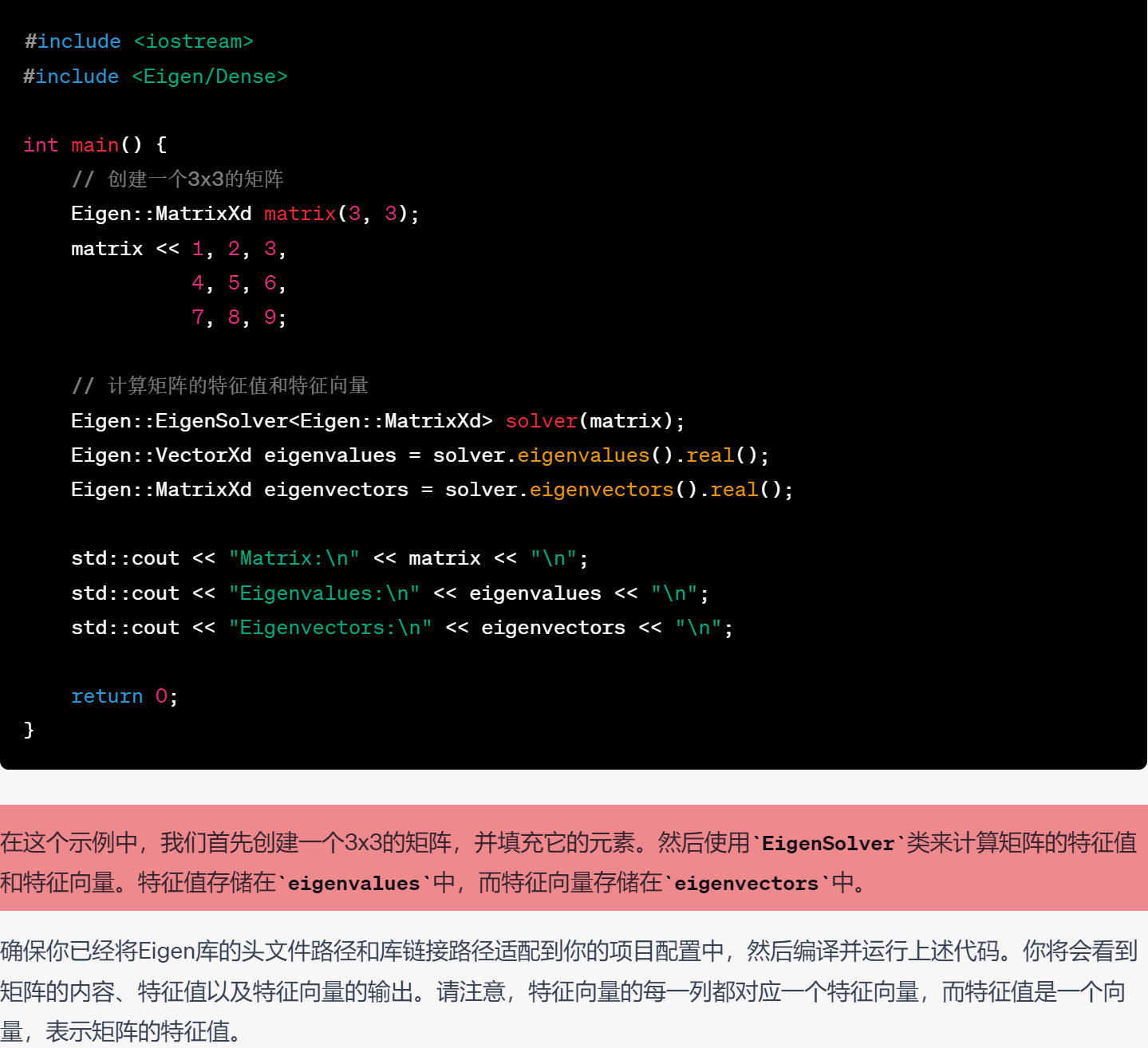
25.使用Eigen库中的SelfAdjointEigenSolver类来计算一个3x3矩阵的特征值和特征向量
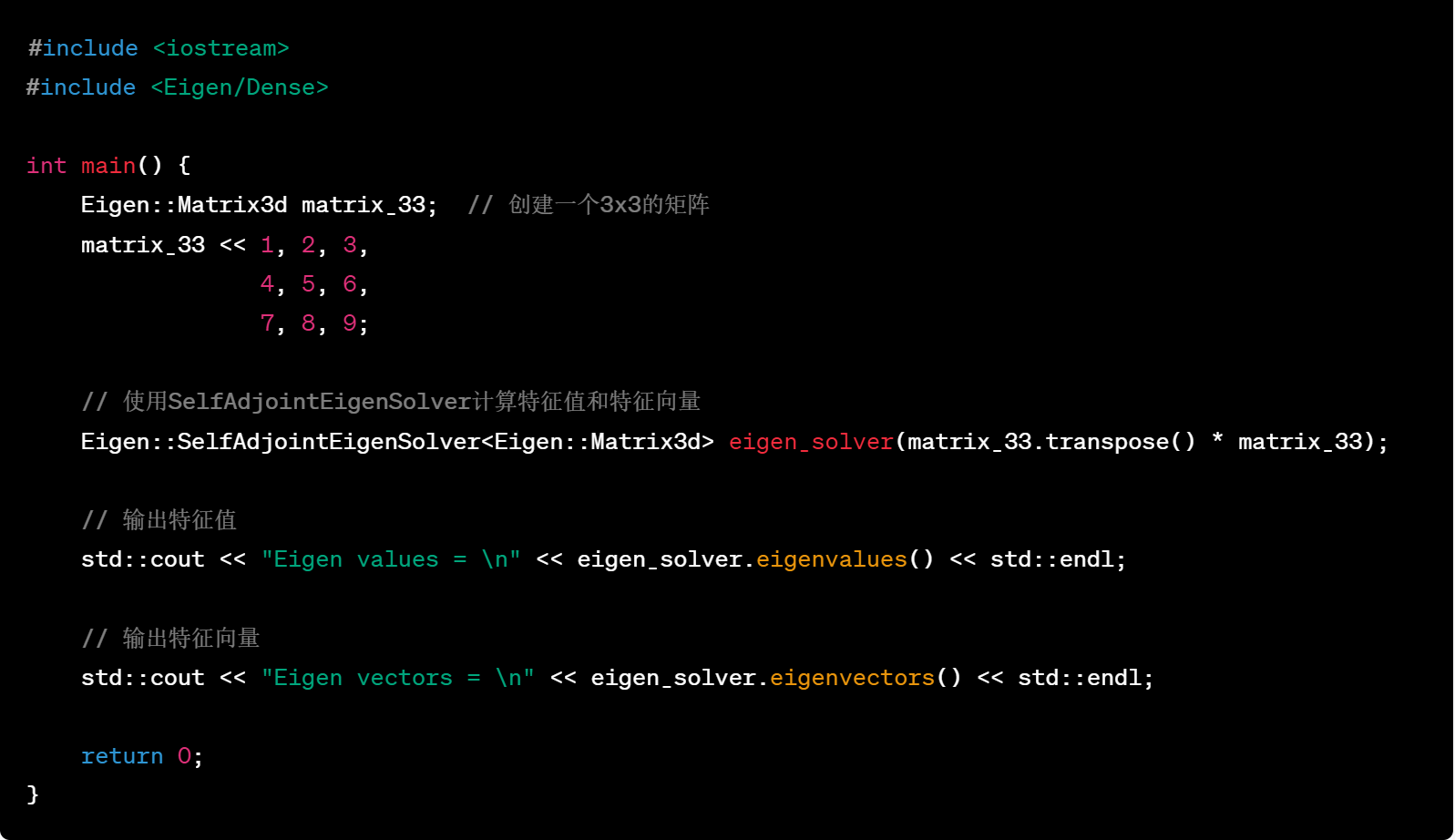
这个示例演示了使用Eigen库中的SelfAdjointEigenSolver类来计算一个3x3矩阵的特征值和特征向量。它首先创建一个对称矩阵 matrix_33,然后通过计算其转置与自身的乘积来准备进行特征值和特征向量计算。
分析:
Eigen::Matrix3d表示一个3x3的矩阵,matrix_33是我们创建的对称矩阵。SelfAdjointEigenSolver<Eigen::Matrix3d>是特征值和特征向量求解器的类型,这里使用SelfAdjointEigenSolver类来处理对称矩阵。eigen_solver是我们创建的特征值和特征向量求解器的实例,它在被构造时会计算给定矩阵的特征值和特征向量。eigen_solver.eigenvalues()用于获取计算得到的特征值,它返回一个向量,表示矩阵的特征值。eigen_solver.eigenvectors()用于获取计算得到的特征向量,它返回一个矩阵,其中每一列是一个特征向量。
确保你已经将Eigen库的头文件路径和库链接路径适配到你的项目配置中,然后编译并运行上述代码。你将会看到特征值和特征向量的输出。这个示例演示了如何使用Eigen库来进行矩阵的特征值和特征向量计算。
26.解线性方程组 Ax = b,使用LU分解

代码
#include <iostream>
#include <Eigen/Dense>
int main() {
// 创建一个系数矩阵A和一个常数向量b
Eigen::MatrixXd A(3, 3);
A << 2, -1, 0,
-1, 2, -1,
0, -1, 2;
Eigen::VectorXd b(3);
b << 1, 2, 3;
// 解线性方程组 Ax = b
Eigen::VectorXd x = A.fullPivLu().solve(b);
std::cout << "Coefficient Matrix A:\n" << A << "\n";
std::cout << "Constant Vector b:\n" << b << "\n";
std::cout << "Solution Vector x:\n" << x << "\n";
return 0;
}
27.解线性方程组 Ax = b,使用QR分解
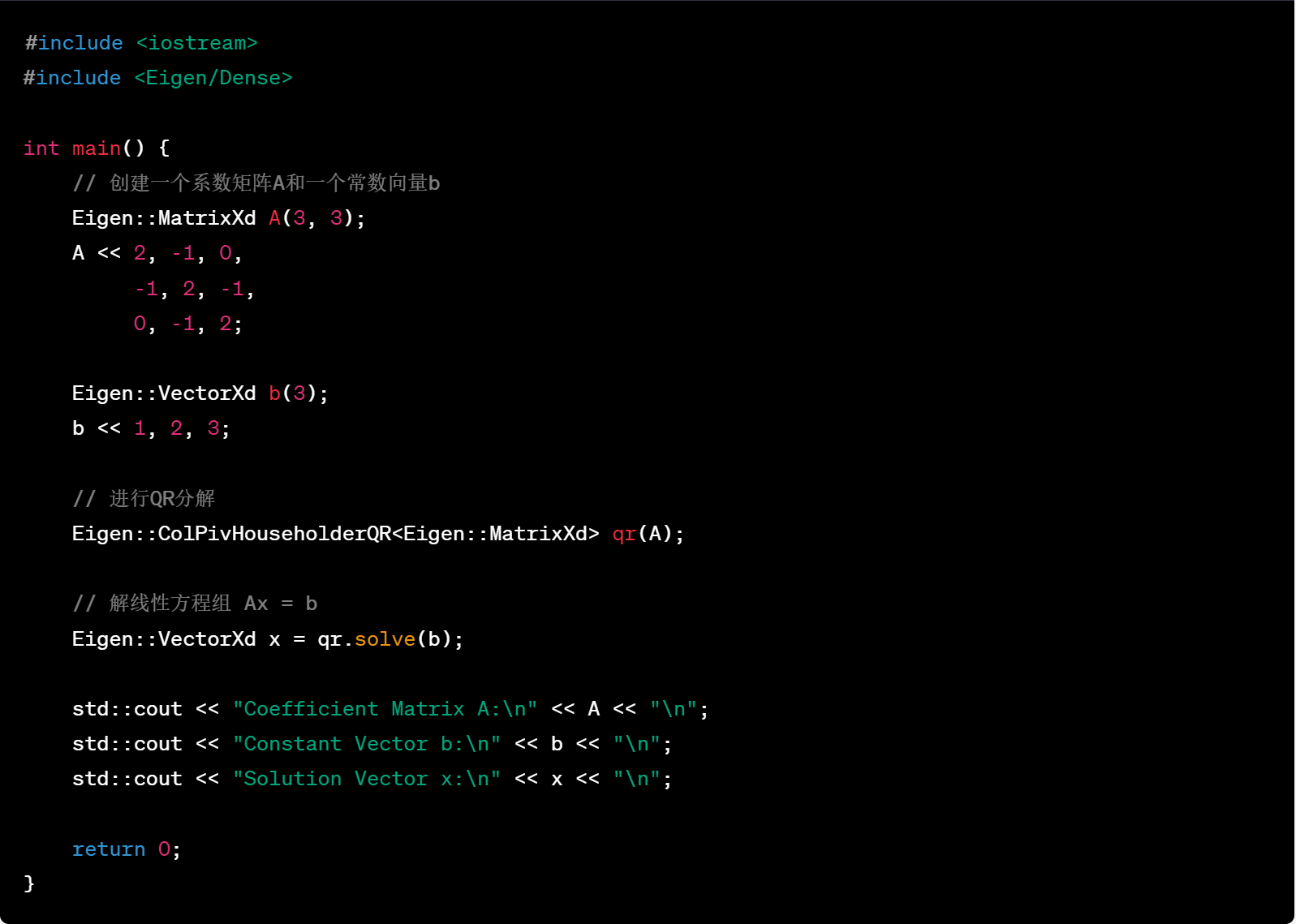
代码
#include <iostream>
#include <Eigen/Dense>
int main() {
// 创建一个系数矩阵A和一个常数向量b
Eigen::MatrixXd A(3, 3);
A << 2, -1, 0,
-1, 2, -1,
0, -1, 2;
Eigen::VectorXd b(3);
b << 1, 2, 3;
// 进行QR分解
Eigen::ColPivHouseholderQR<Eigen::MatrixXd> qr(A);
// 解线性方程组 Ax = b
Eigen::VectorXd x = qr.solve(b);
std::cout << "Coefficient Matrix A:\n" << A << "\n";
std::cout << "Constant Vector b:\n" << b << "\n";
std::cout << "Solution Vector x:\n" << x << "\n";
return 0;
}
27.解线性方程组 Ax = b,使用Cholesky分解
在C++中,你可以使用Eigen库进行Cholesky分解来解决线性方程组。Cholesky分解是一种用于对称正定矩阵的分解方法,可以有效地解决线性方程组。以下是一个使用Eigen库进行Cholesky分解解线性方程组的示例代码:
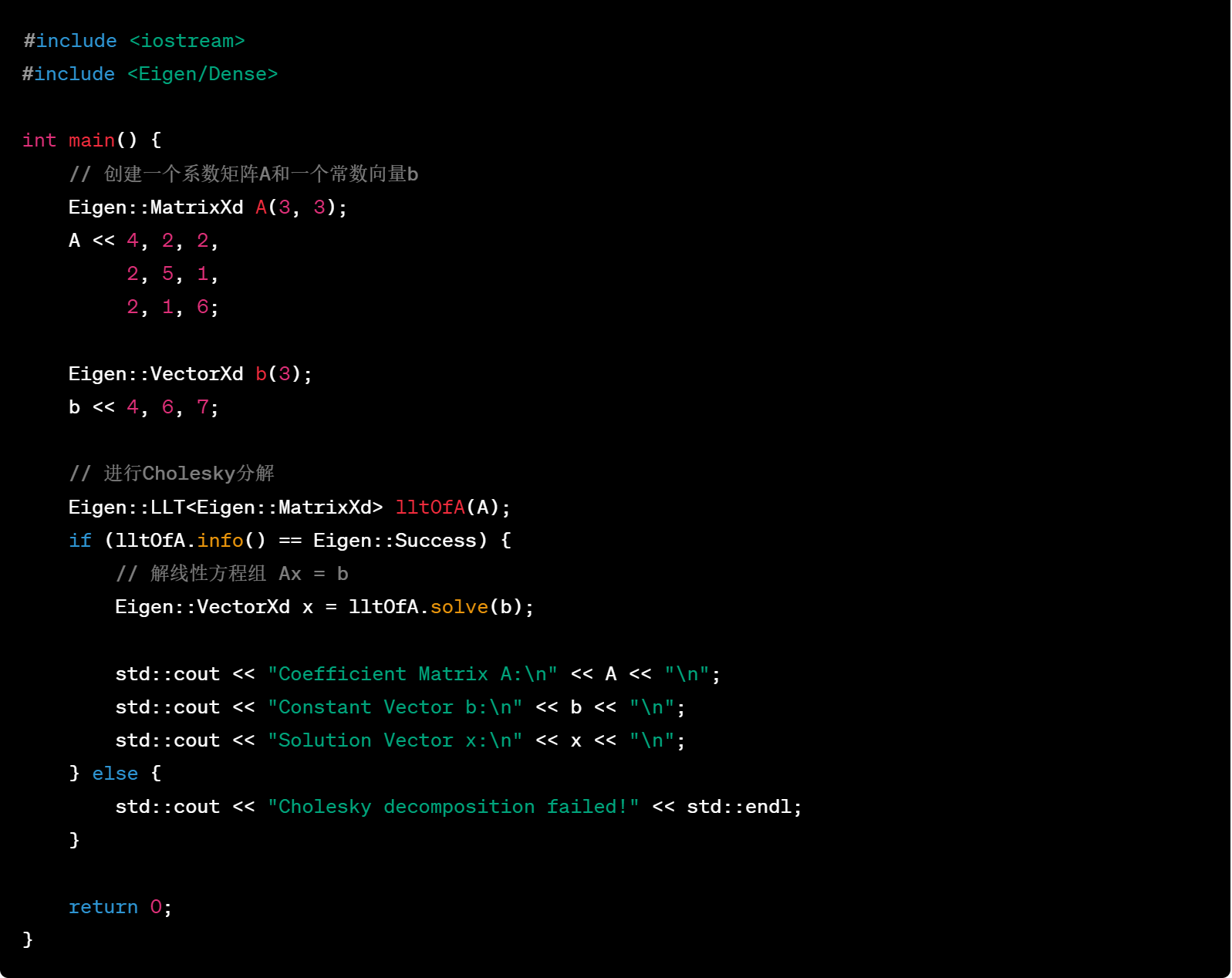
在这个示例中,我们首先创建一个系数矩阵 A 和一个常数向量 b,代表线性方程组 Ax = b。然后使用LLT类进行Cholesky分解,如果分解成功(正定矩阵才能成功分解),就调用solve(b)方法来解线性方程组并计算得到解向量 x。
请注意,Cholesky分解适用于对称正定矩阵。在使用之前,你应该确保矩阵 A 是对称正定的。如果矩阵不满足这些条件,Cholesky分解将会失败。
确保你已经将Eigen库的头文件路径和库链接路径适配到你的项目配置中,然后编译并运行上述代码。你将会看到系数矩阵、常数向量和解向量的输出。这个示例演示了如何使用Eigen库进行Cholesky分解来解决线性方程组。
代码
#include <iostream>
#include <Eigen/Dense>
int main() {
// 创建一个系数矩阵A和一个常数向量b
Eigen::MatrixXd A(3, 3);
A << 4, 2, 2,
2, 5, 1,
2, 1, 6;
Eigen::VectorXd b(3);
b << 4, 6, 7;
// 进行Cholesky分解
Eigen::LLT<Eigen::MatrixXd> lltOfA(A);
if (lltOfA.info() == Eigen::Success) {
// 解线性方程组 Ax = b
Eigen::VectorXd x = lltOfA.solve(b);
std::cout << "Coefficient Matrix A:\n" << A << "\n";
std::cout << "Constant Vector b:\n" << b << "\n";
std::cout << "Solution Vector x:\n" << x << "\n";
} else {
std::cout << "Cholesky decomposition failed!" << std::endl;
}
return 0;
}
28.将旋转向量转为旋转矩阵
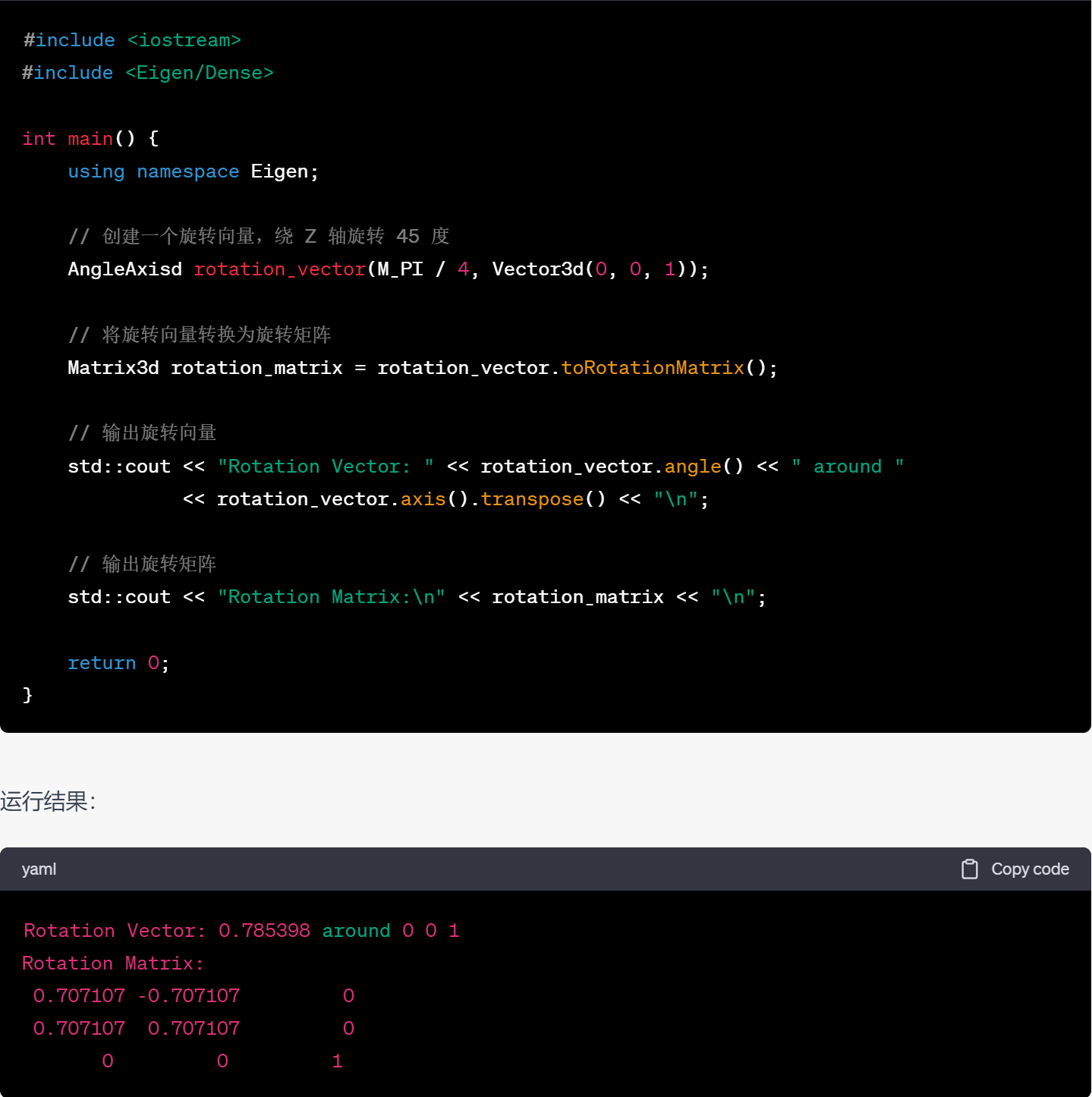
代码
#include <iostream>
#include <Eigen/Dense>
int main() {
using namespace Eigen;
// 创建一个旋转向量,绕 Z 轴旋转 45 度
AngleAxisd rotation_vector(M_PI / 4, Vector3d(0, 0, 1));
// 将旋转向量转换为旋转矩阵
Matrix3d rotation_matrix = rotation_vector.toRotationMatrix();
// 输出旋转向量
std::cout << "Rotation Vector: " << rotation_vector.angle() << " around "
<< rotation_vector.axis().transpose() << "\n";
// 输出旋转矩阵
std::cout << "Rotation Matrix:\n" << rotation_matrix << "\n";
return 0;
}
29.将旋转矩阵转为旋转向量
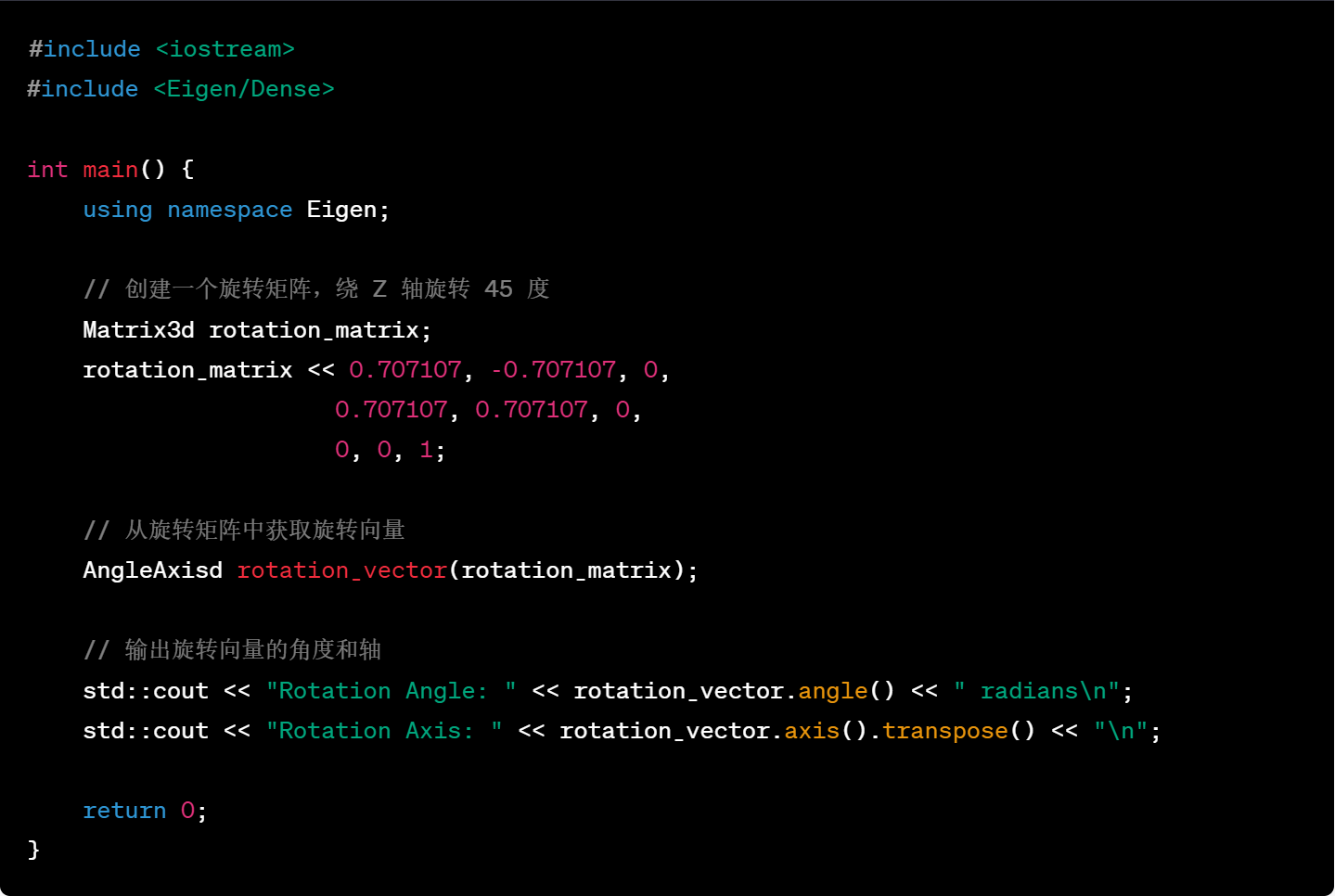
代码
#include <iostream>
#include <Eigen/Dense>
int main() {
using namespace Eigen;
// 创建一个旋转矩阵,绕 Z 轴旋转 45 度
Matrix3d rotation_matrix;
rotation_matrix << 0.707107, -0.707107, 0,
0.707107, 0.707107, 0,
0, 0, 1;
// 从旋转矩阵中获取旋转向量
AngleAxisd rotation_vector(rotation_matrix);
// 输出旋转向量的角度和轴
std::cout << "Rotation Angle: " << rotation_vector.angle() << " radians\n";
std::cout << "Rotation Axis: " << rotation_vector.axis().transpose() << "\n";
return 0;
}
30.使用旋转向量对向量进行旋转的坐标变换
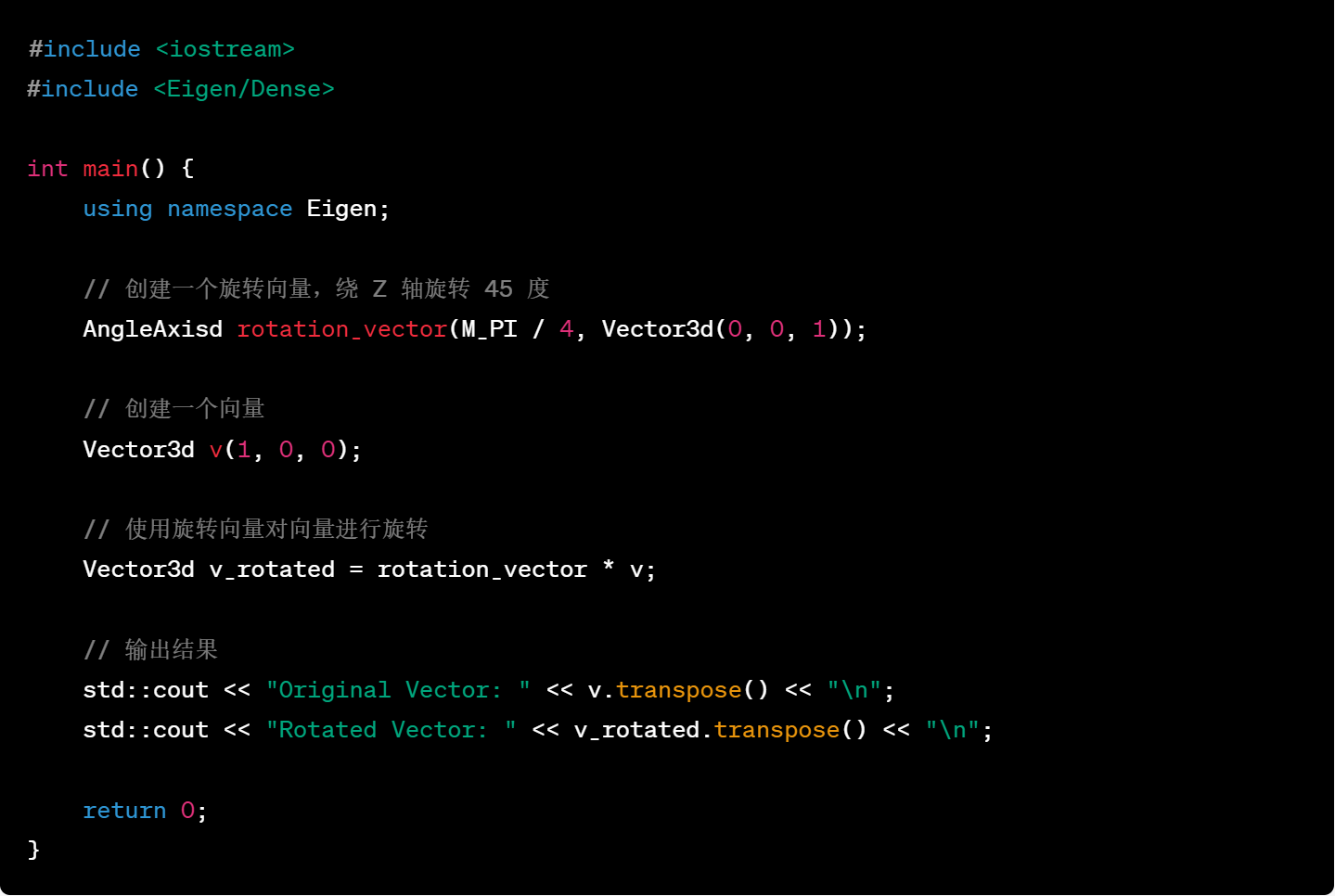
31.将旋转矩阵转换为欧拉角
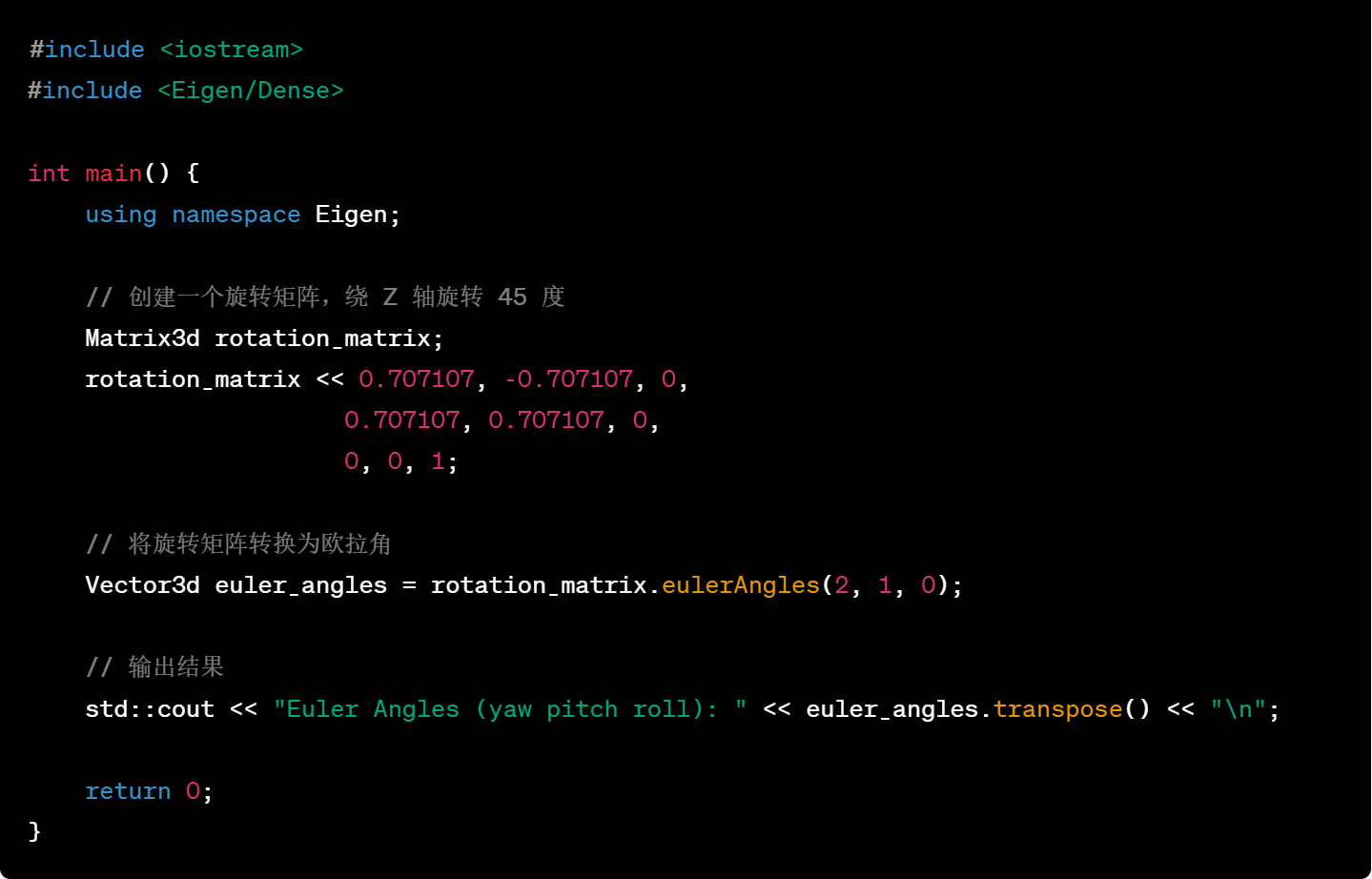
32.创建欧氏变换矩阵
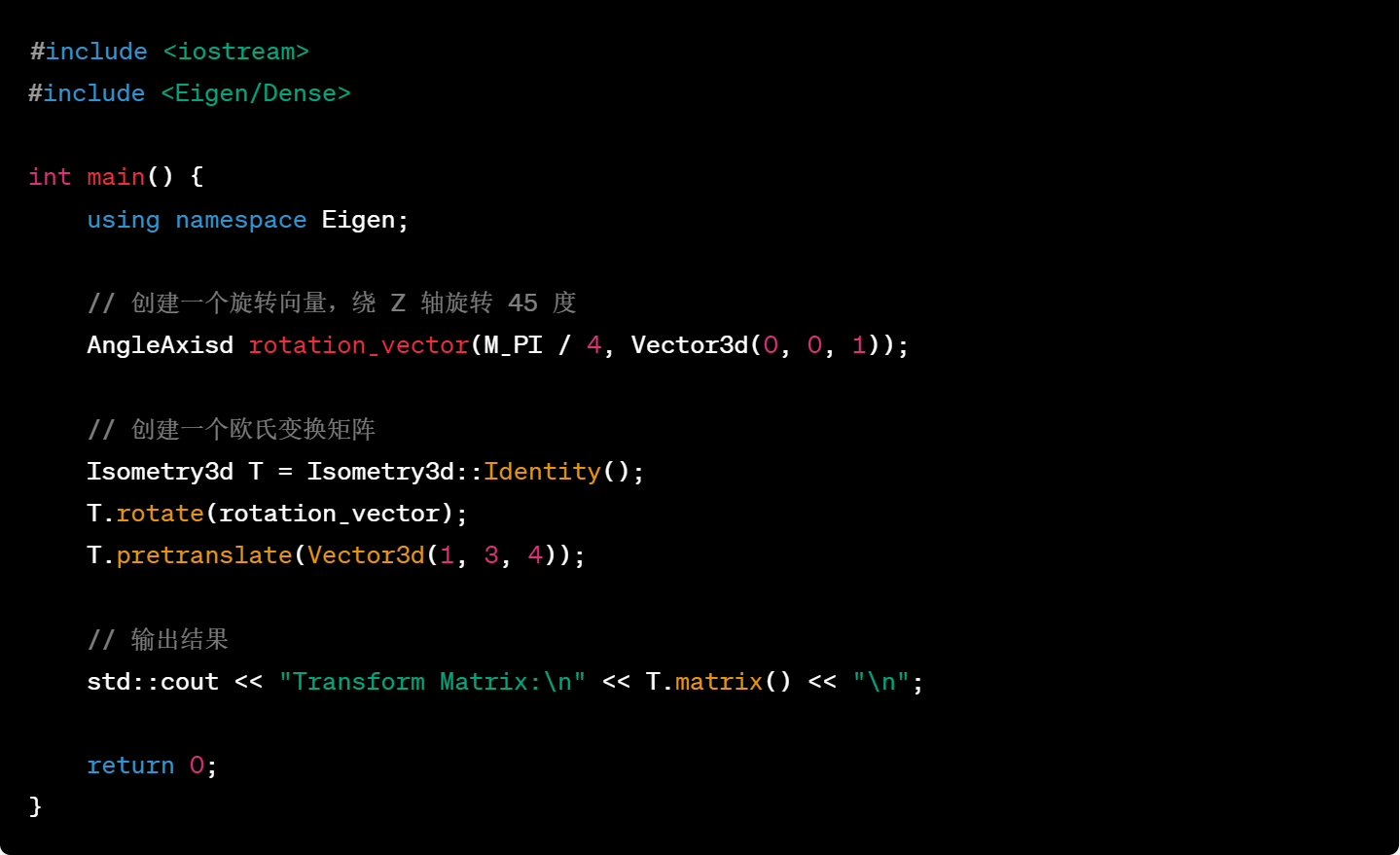
33.使用变换矩阵进行坐标变换
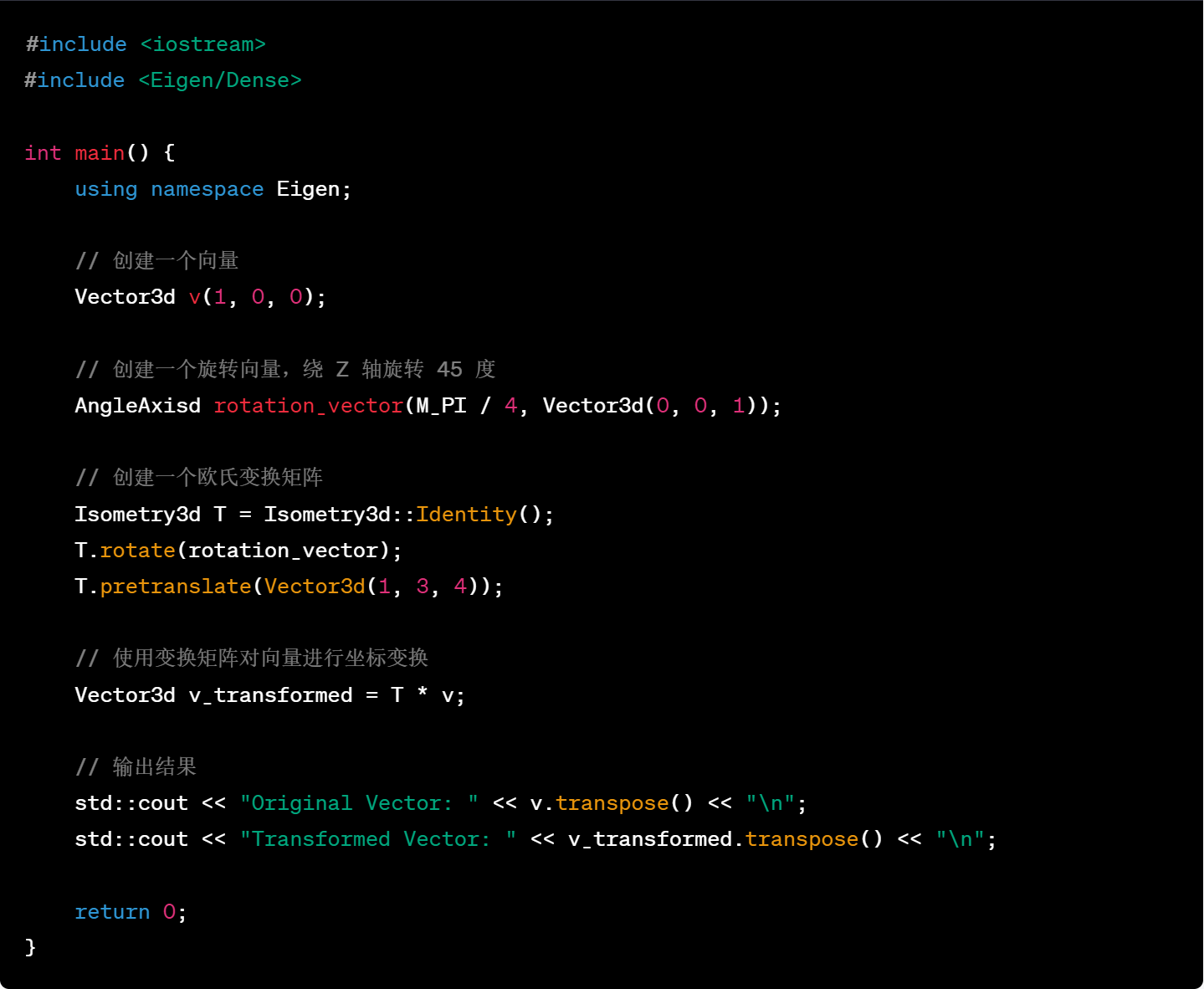
34.创建四元数
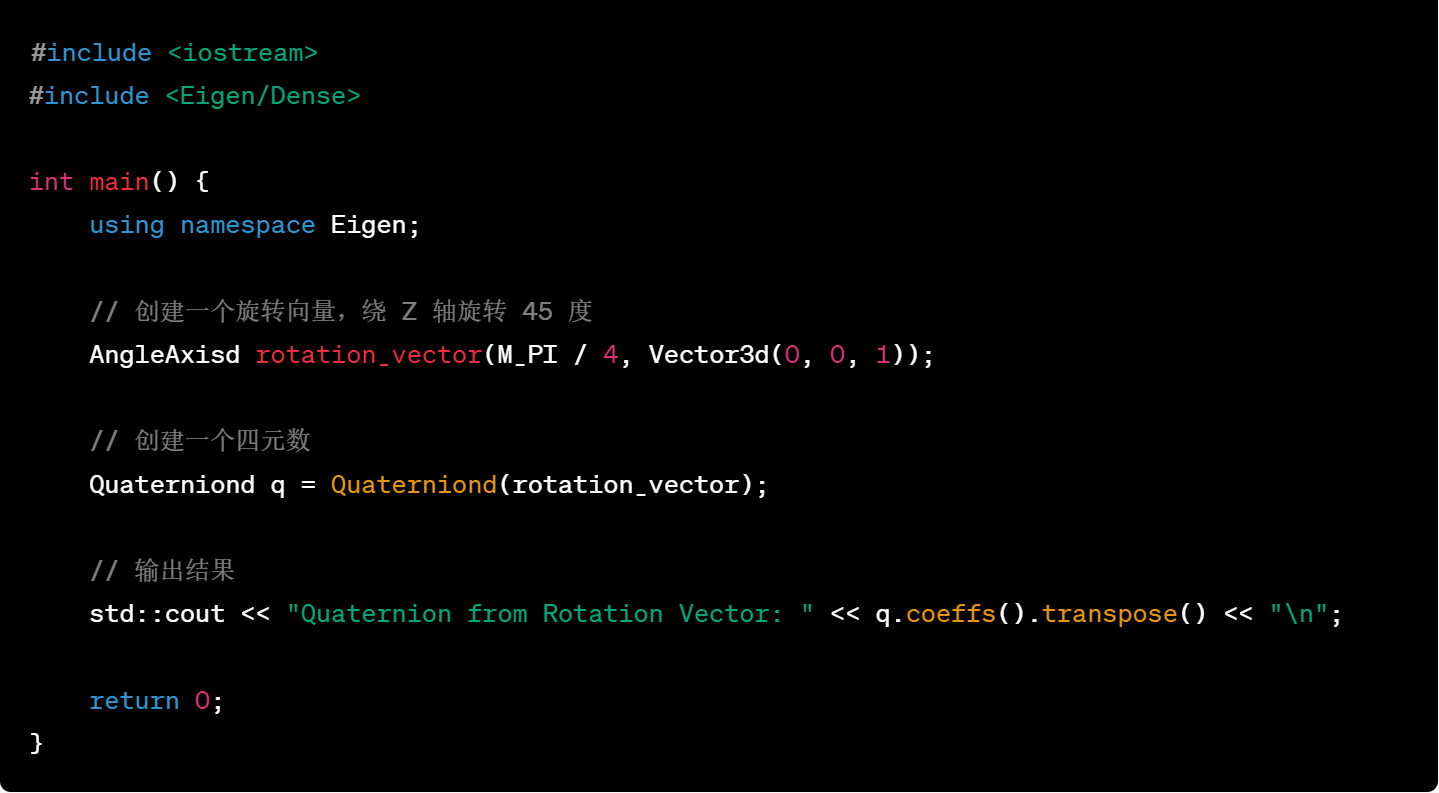
35.使用四元数旋转向量
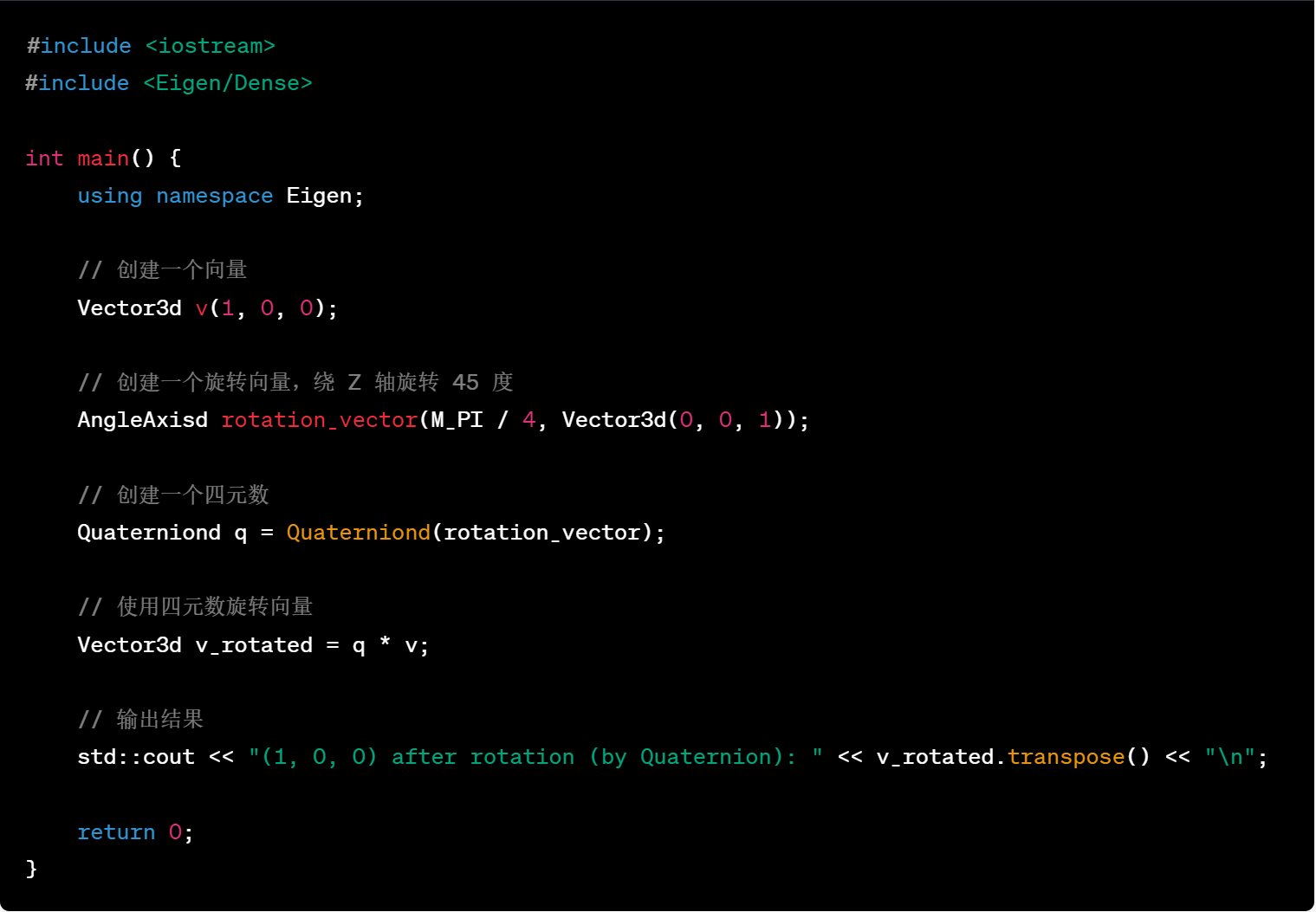
36.使用刚体变换(欧氏变换)来进行旋转和平移操作
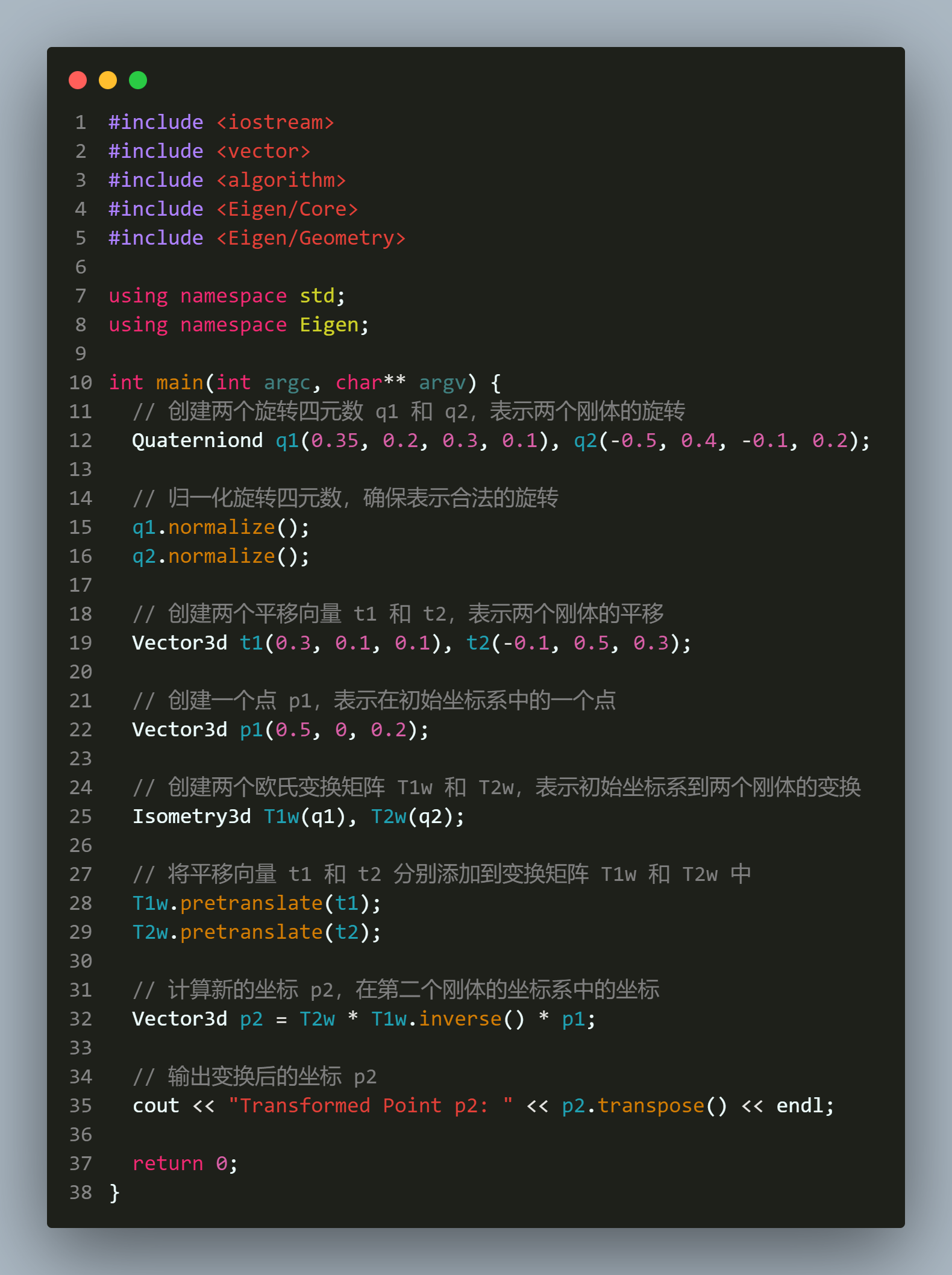
代码
#include <iostream>
#include <vector>
#include <algorithm>
#include <Eigen/Core>
#include <Eigen/Geometry>
using namespace std;
using namespace Eigen;
int main(int argc, char** argv) {
// 创建两个旋转四元数 q1 和 q2,表示两个刚体的旋转
Quaterniond q1(0.35, 0.2, 0.3, 0.1), q2(-0.5, 0.4, -0.1, 0.2);
// 归一化旋转四元数,确保表示合法的旋转
q1.normalize();
q2.normalize();
// 创建两个平移向量 t1 和 t2,表示两个刚体的平移
Vector3d t1(0.3, 0.1, 0.1), t2(-0.1, 0.5, 0.3);
// 创建一个点 p1,表示在初始坐标系中的一个点
Vector3d p1(0.5, 0, 0.2);
// 创建两个欧氏变换矩阵 T1w 和 T2w,表示初始坐标系到两个刚体的变换
Isometry3d T1w(q1), T2w(q2);
// 将平移向量 t1 和 t2 分别添加到变换矩阵 T1w 和 T2w 中
T1w.pretranslate(t1);
T2w.pretranslate(t2);
// 计算新的坐标 p2,在第二个刚体的坐标系中的坐标
Vector3d p2 = T2w * T1w.inverse() * p1;
// 输出变换后的坐标 p2
cout << "Transformed Point p2: " << p2.transpose() << endl;
return 0;
}
37.eigen的数据类型
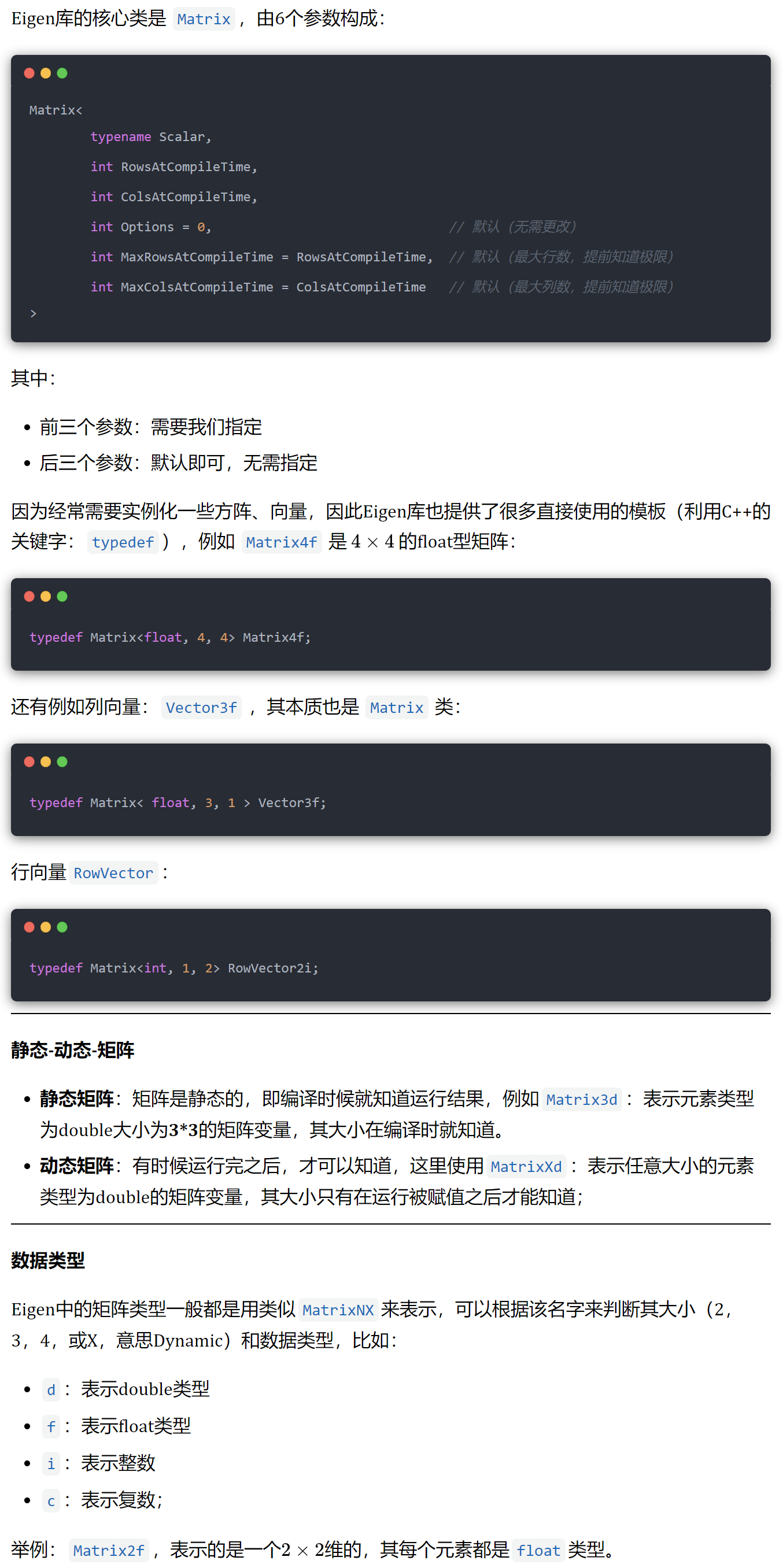
38.eigen的block()函数
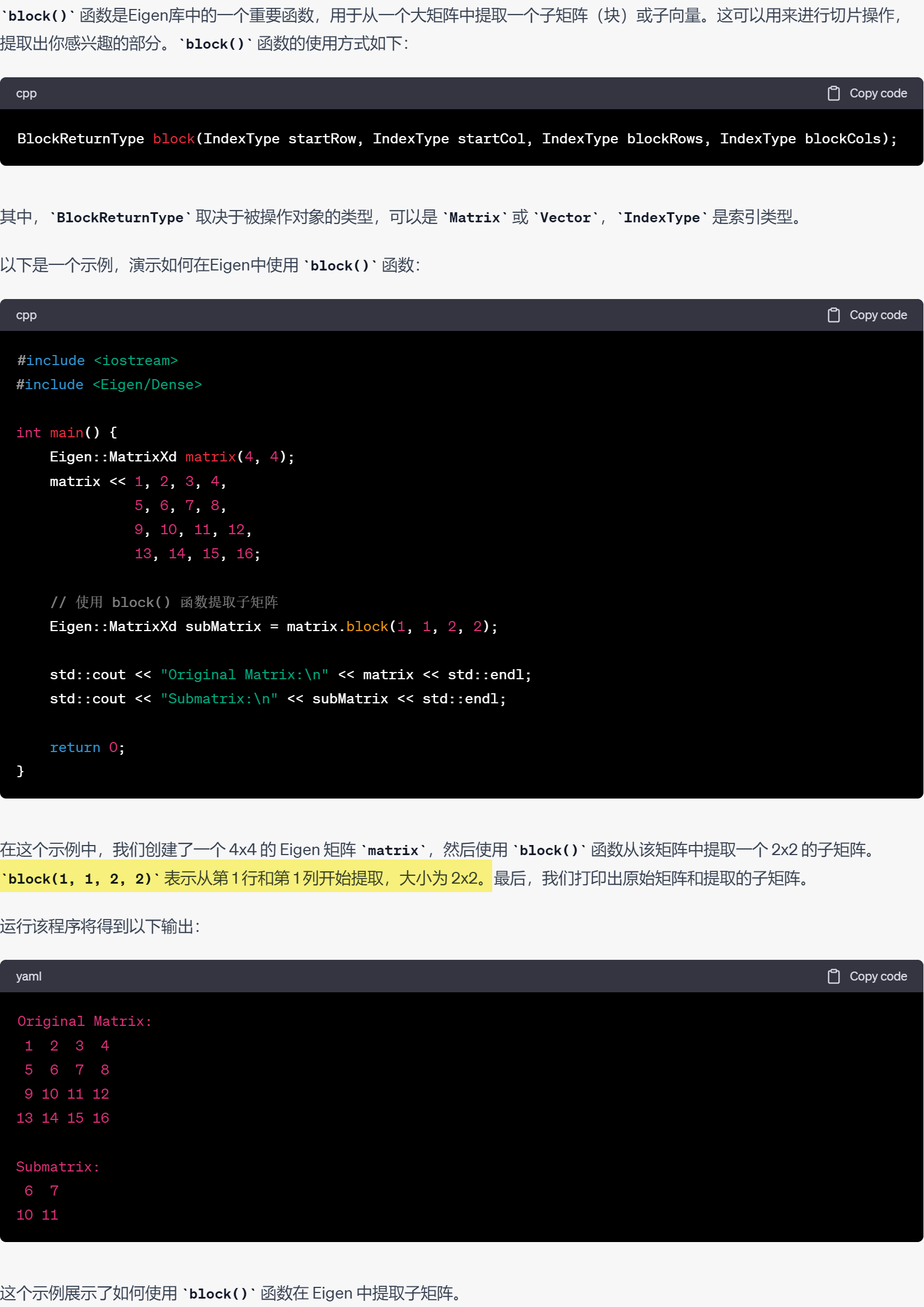
39.eigen中的.col()和.row()方法
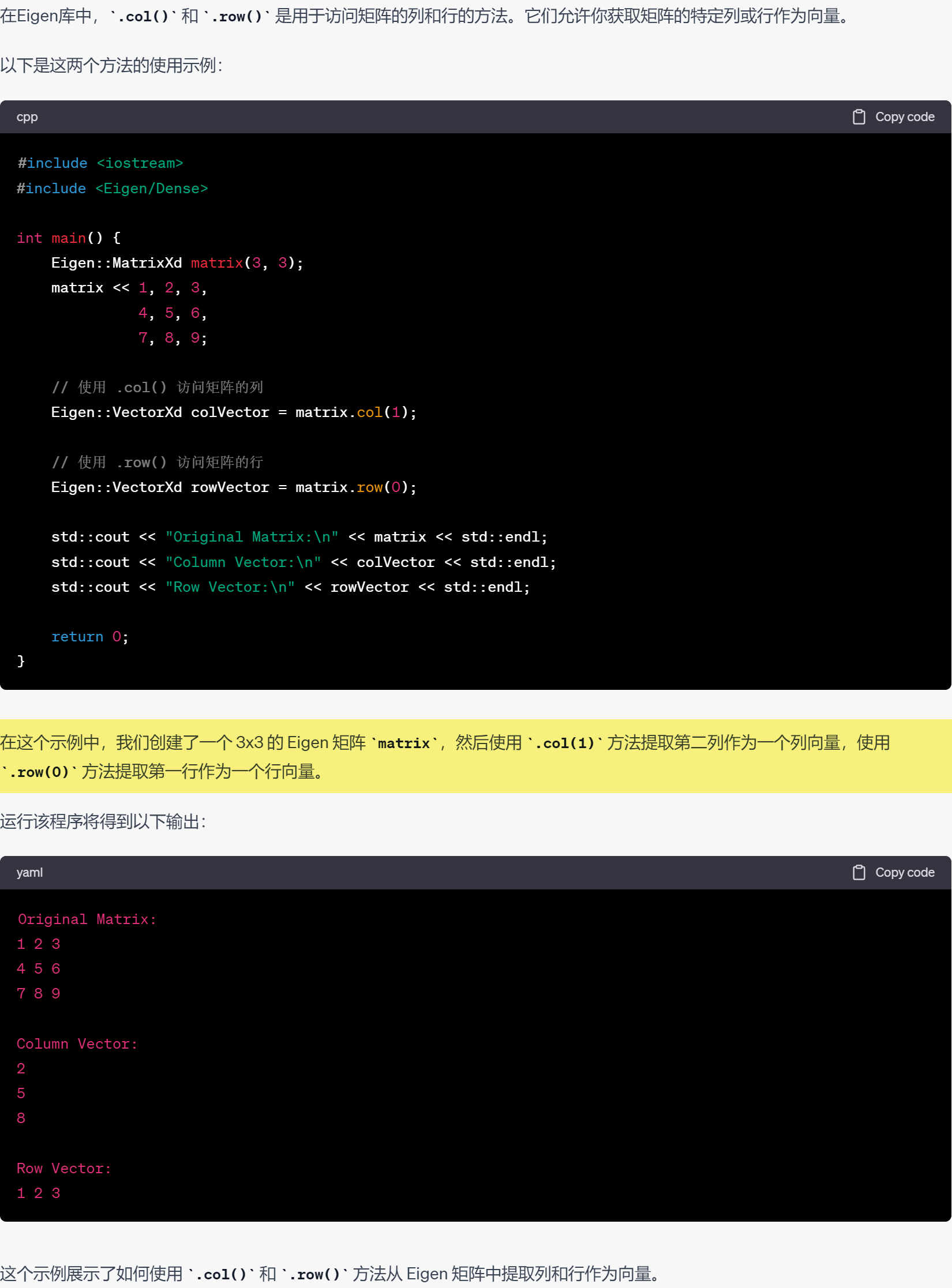
40.eigen的点乘和叉乘.dot()和.cross()
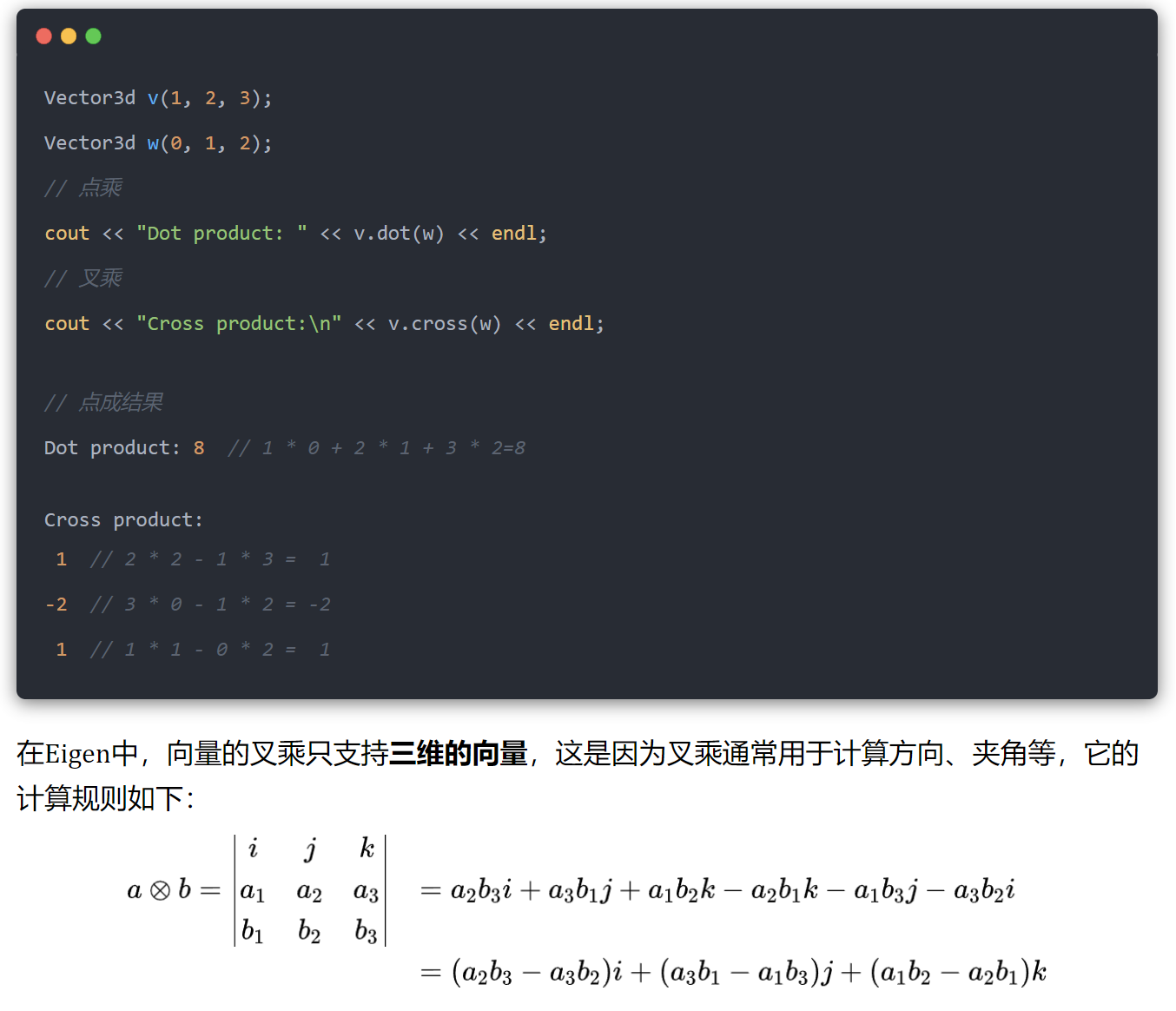
41.元素乘积.prod()——即向量中所有元素的乘积
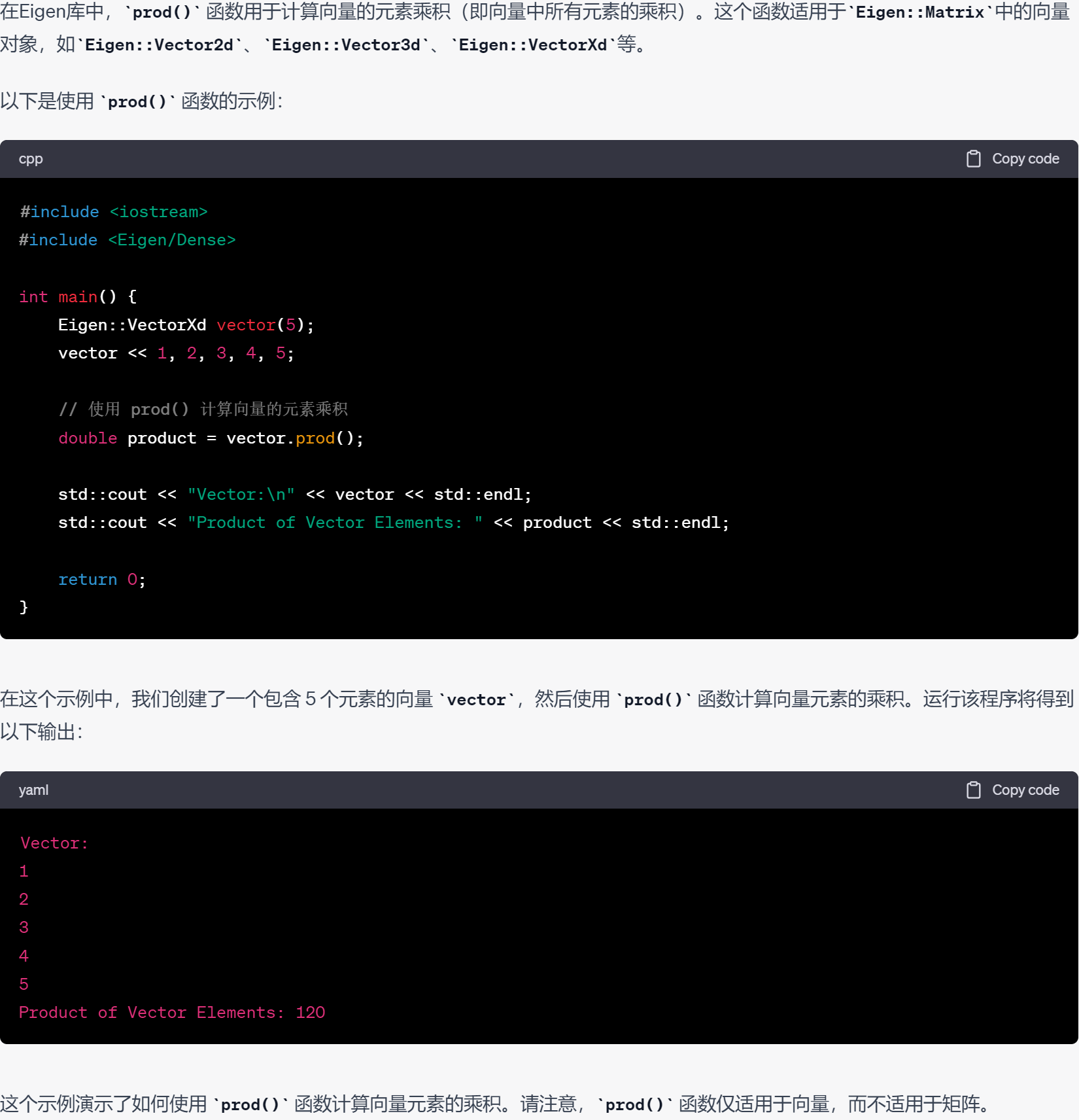
42.元素均值.mean()
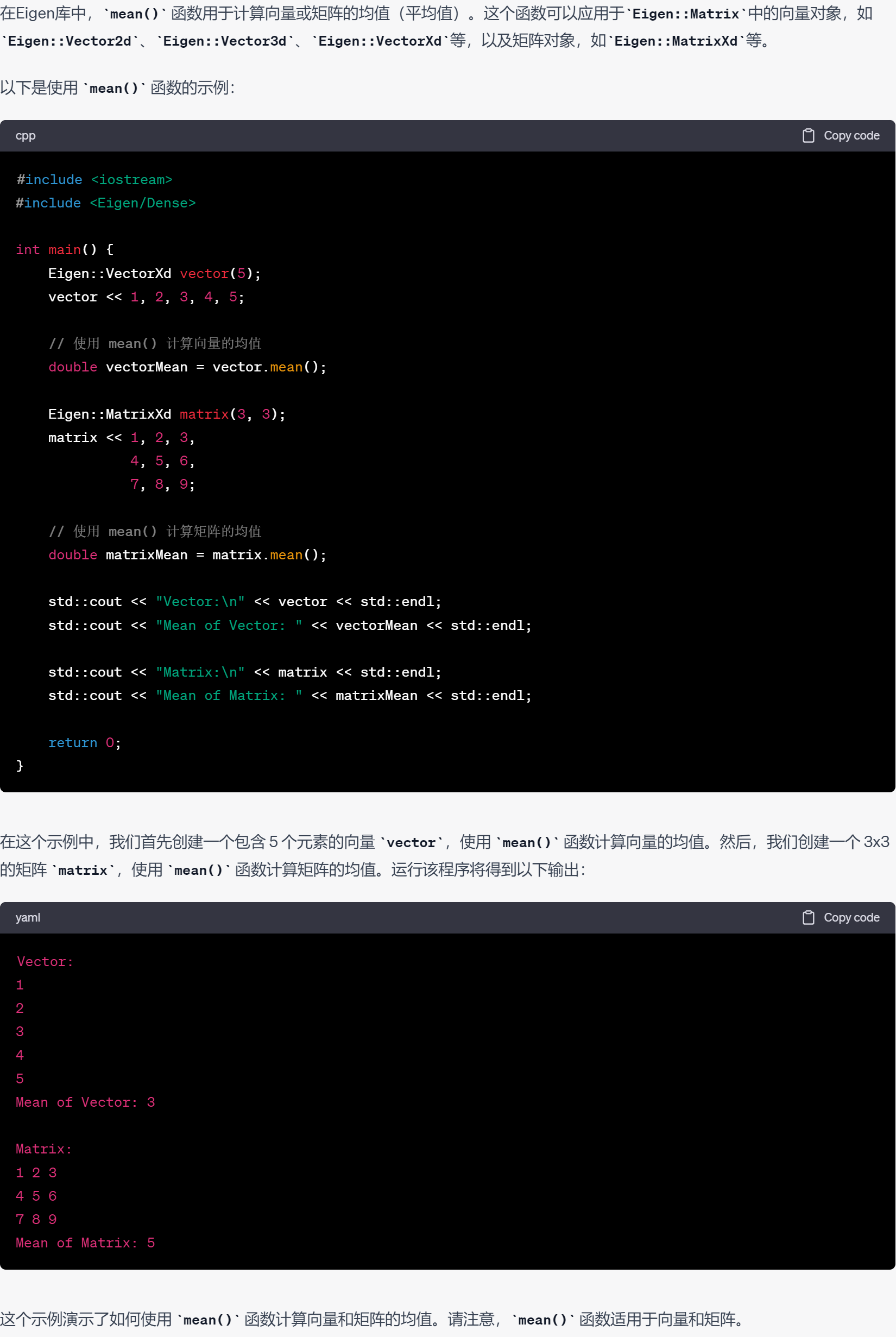
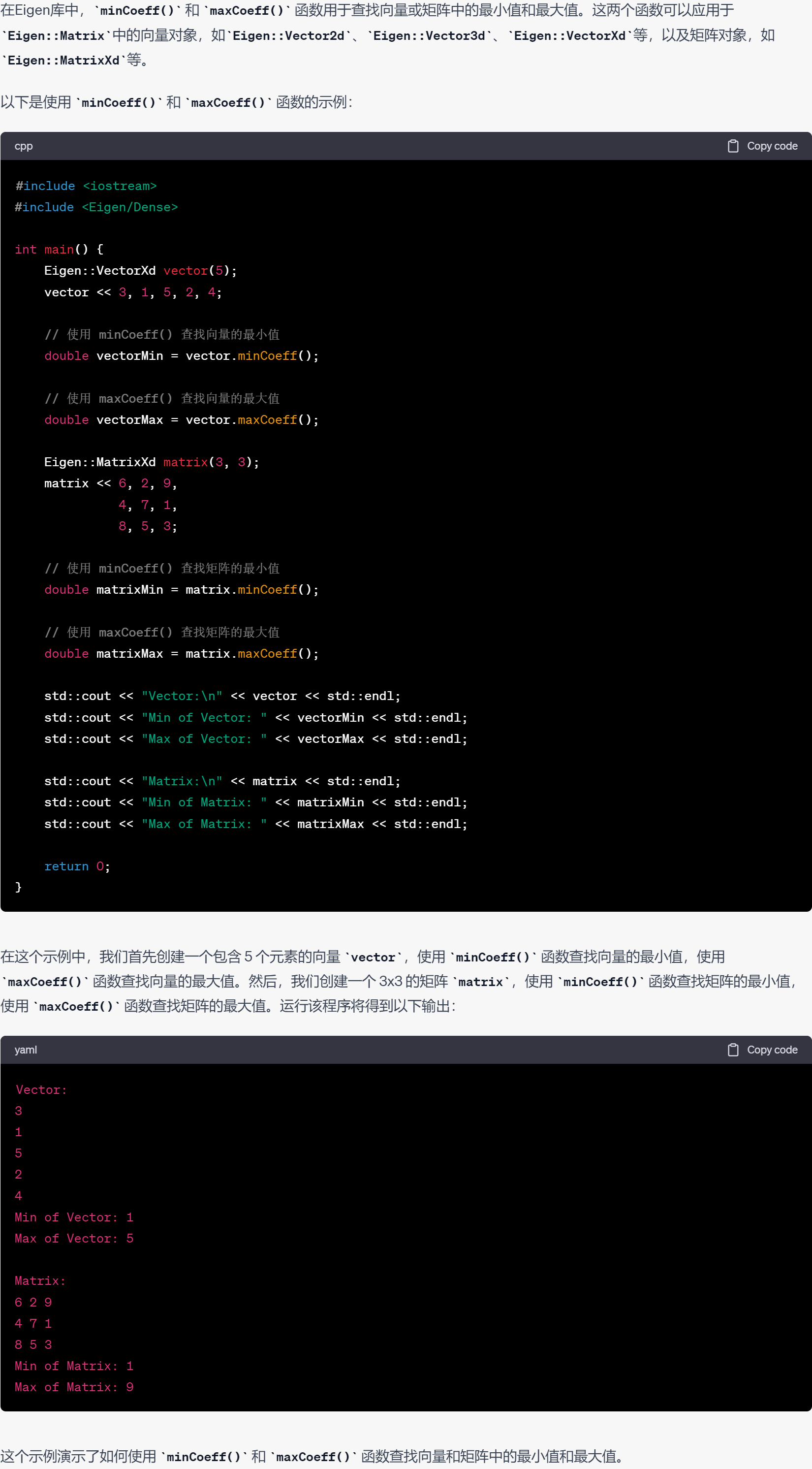
43.查找向量或矩阵中的最小值和最大值minCoeff()和maxCoeff()
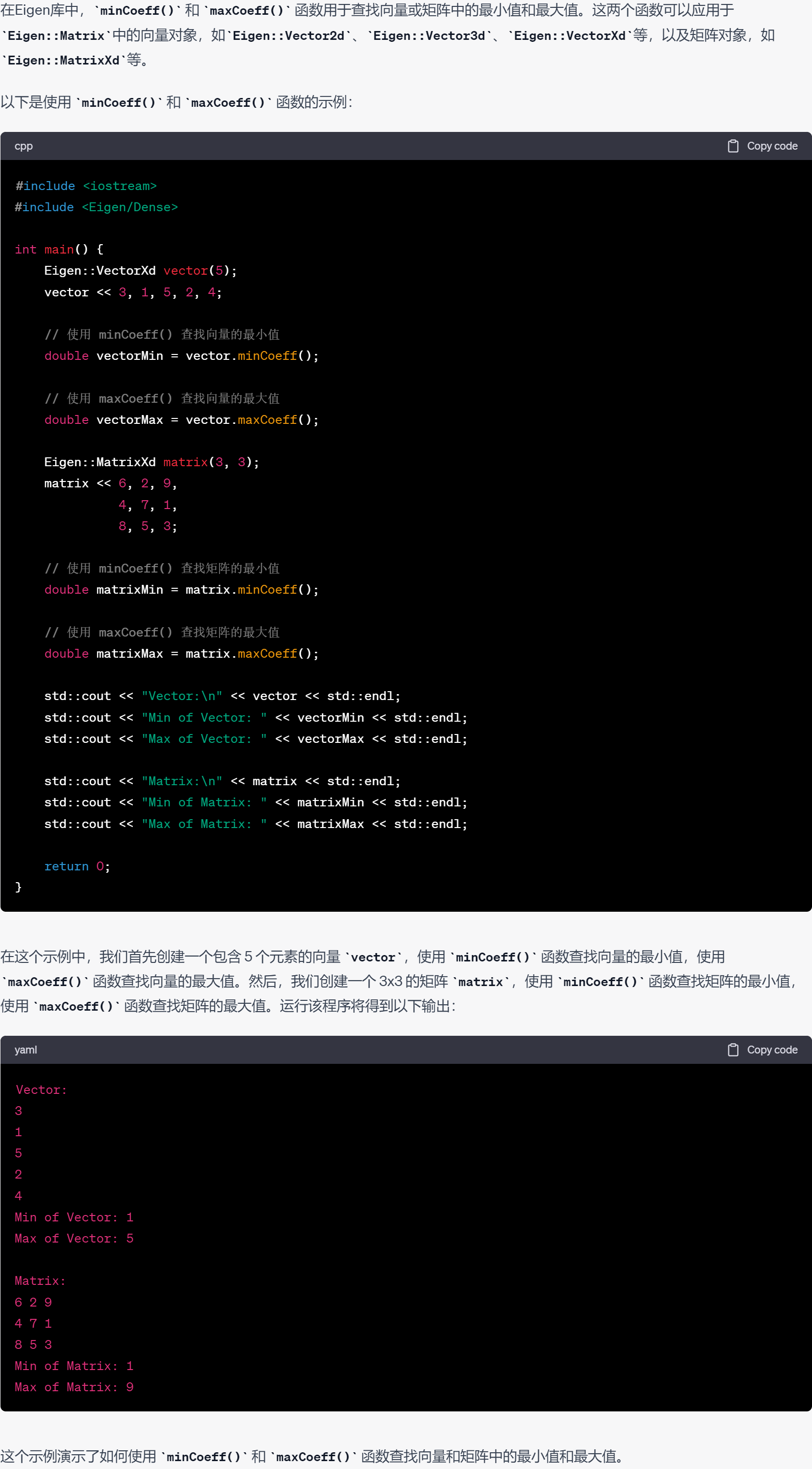
44.生成随机矩阵random()
45.用于处理数组(元素级操作)的数据结构Array类
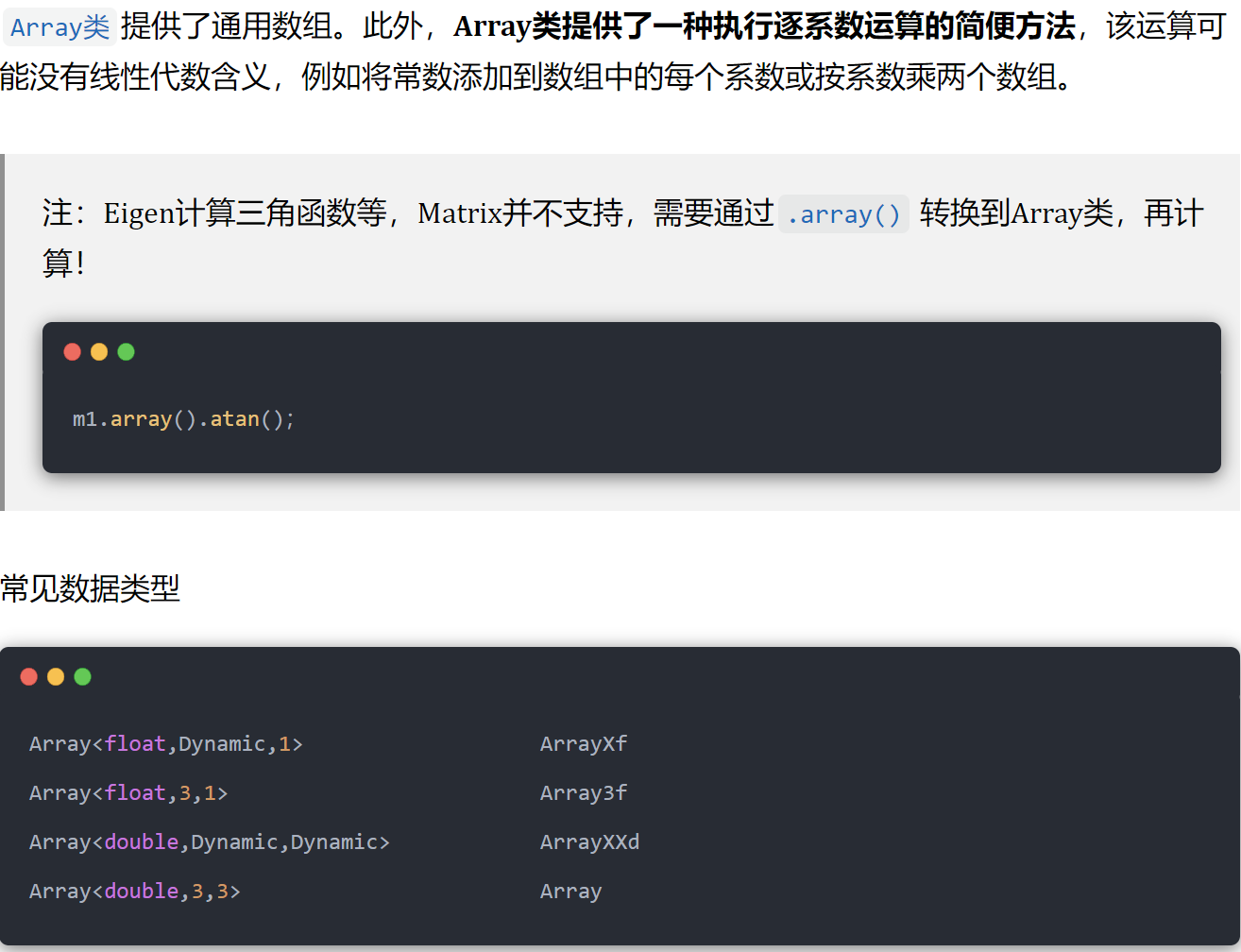
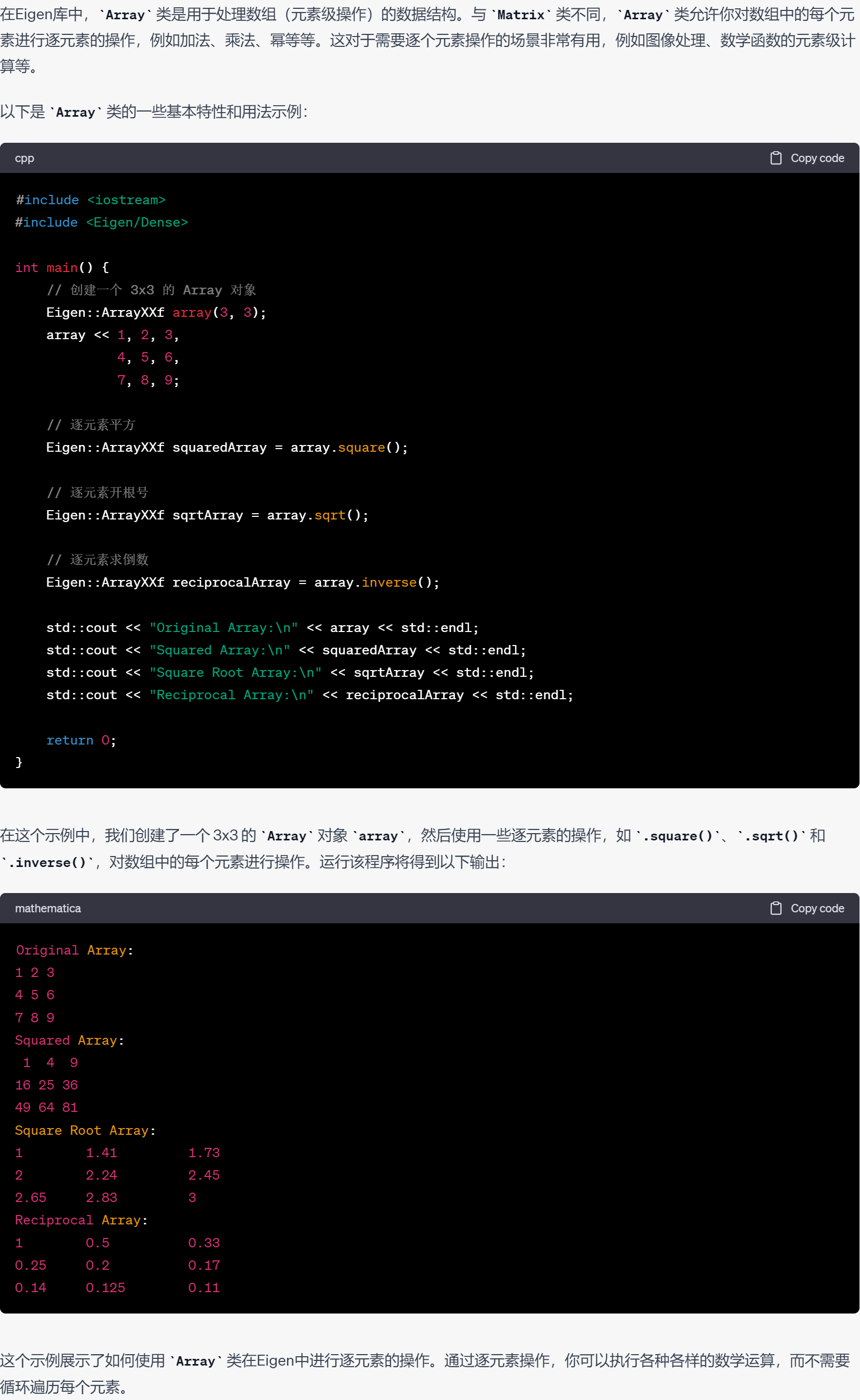
46.eigen中Array类的常见操作
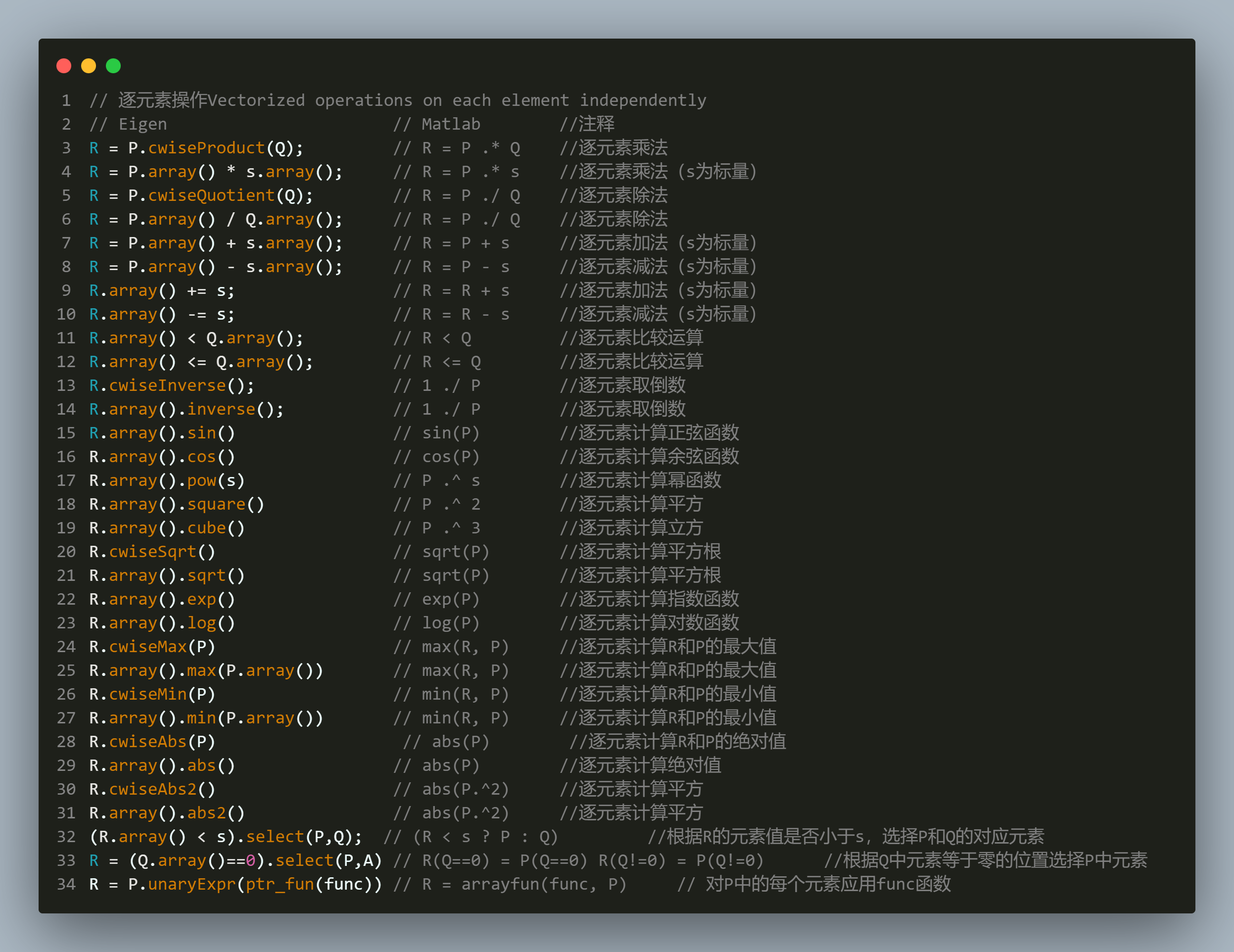
代码
// 逐元素操作Vectorized operations on each element independently
// Eigen // Matlab //注释
R = P.cwiseProduct(Q); // R = P .* Q //逐元素乘法
R = P.array() * s.array(); // R = P .* s //逐元素乘法(s为标量)
R = P.cwiseQuotient(Q); // R = P ./ Q //逐元素除法
R = P.array() / Q.array(); // R = P ./ Q //逐元素除法
R = P.array() + s.array(); // R = P + s //逐元素加法(s为标量)
R = P.array() - s.array(); // R = P - s //逐元素减法(s为标量)
R.array() += s; // R = R + s //逐元素加法(s为标量)
R.array() -= s; // R = R - s //逐元素减法(s为标量)
R.array() < Q.array(); // R < Q //逐元素比较运算
R.array() <= Q.array(); // R <= Q //逐元素比较运算
R.cwiseInverse(); // 1 ./ P //逐元素取倒数
R.array().inverse(); // 1 ./ P //逐元素取倒数
R.array().sin() // sin(P) //逐元素计算正弦函数
R.array().cos() // cos(P) //逐元素计算余弦函数
R.array().pow(s) // P .^ s //逐元素计算幂函数
R.array().square() // P .^ 2 //逐元素计算平方
R.array().cube() // P .^ 3 //逐元素计算立方
R.cwiseSqrt() // sqrt(P) //逐元素计算平方根
R.array().sqrt() // sqrt(P) //逐元素计算平方根
R.array().exp() // exp(P) //逐元素计算指数函数
R.array().log() // log(P) //逐元素计算对数函数
R.cwiseMax(P) // max(R, P) //逐元素计算R和P的最大值
R.array().max(P.array()) // max(R, P) //逐元素计算R和P的最大值
R.cwiseMin(P) // min(R, P) //逐元素计算R和P的最小值
R.array().min(P.array()) // min(R, P) //逐元素计算R和P的最小值
R.cwiseAbs(P) // abs(P) //逐元素计算R和P的绝对值
R.array().abs() // abs(P) //逐元素计算绝对值
R.cwiseAbs2() // abs(P.^2) //逐元素计算平方
R.array().abs2() // abs(P.^2) //逐元素计算平方
(R.array() < s).select(P,Q); // (R < s ? P : Q) //根据R的元素值是否小于s,选择P和Q的对应元素
R = (Q.array()==0).select(P,A) // R(Q==0) = P(Q==0) R(Q!=0) = P(Q!=0) //根据Q中元素等于零的位置选择P中元素
R = P.unaryExpr(ptr_fun(func)) // R = arrayfun(func, P) // 对P中的每个元素应用func函数
参考链接:一文学会Eigen库