樽海鞘算法的主要灵感是樽海鞘在海洋中航行和觅食时的群聚行为。相关文献表示，多目标优化之樽海鞘算法的结果表明，该算法可以逼近帕雷托最优解，收敛性和覆盖率高。

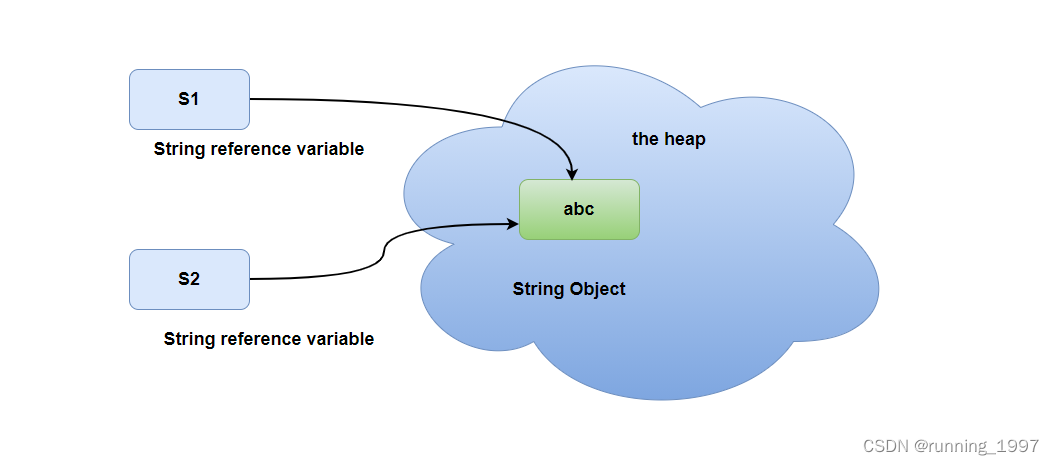
通过给SSA算法配备一个食物来源库来解决第一个问题。该存储库维护了到目前为止优化过程中获得的最优解，非常类似于多目标粒子群优化(MOPSO)中的存档。存储库有一个最大大小来存储数量有限的最优解决方案。在优化过程中，使用Pareto优势操作符将每个樽海鞘与所有存储库原方案进行比较。

• 如果一个樽海鞘在存储库中占优，则必须交换它们（把樽海鞘放入存储库，原方案拿出）。如果一个樽海鞘在存储库中优于一组解决方案，那么应该将这一组解决方案全部从存储库中删除，并把该樽海鞘应该添加到存储库中。

• 如果至少有一个存储库中的原方案比该樽海鞘更优，那么该樽海鞘应被丢弃，不加入存储库。

• 如果与所有存储库居民相比，该樽海鞘与之互不占优，那么该樽海鞘即是最优解，则必须将其添加到存储库中。

这些规则可以保证存储库得到的始终都是目前为止算法所获得的最优解决方案。但是，有一种特殊情况，即存储库已满，与存储库原方案相比，该樽海鞘也不占优，此时本应该将该樽海鞘加入存储库，但是存储库满了。当然，最简单的方法是随机删除归档中的一个解决方案，并将其替换为这个樽海鞘。

由此可见，多目标樽海鞘算法与多目标灰狼算法一致，也是采用的网格机制。大家可以对比学习。

多目标樽海鞘在ZDT1中的表现：

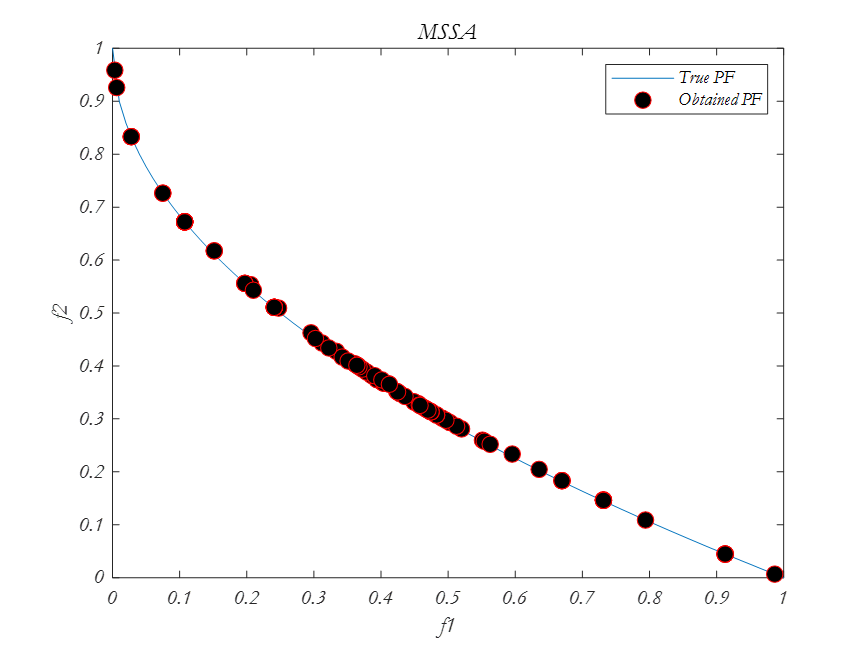
主函数代码：

clc
clear
close all


% Change these details with respect to your problem
ObjectiveFunction=@ZDT1;
dim=5;
lb=0;
ub=1;
obj_no=2;


if size(ub,2)==1
    ub=ones(1,dim)*ub;
    lb=ones(1,dim)*lb;
end


max_iter=100;
N=200;
ArchiveMaxSize=100;
Archive_X=zeros(100,dim);
Archive_F=ones(100,obj_no)*inf;
Archive_member_no=0;
r=(ub-lb)/2;
V_max=(ub(1)-lb(1))/10;
Food_fitness=inf*ones(1,obj_no);
Food_position=zeros(dim,1);
Salps_X=initialization(N,dim,ub,lb);
fitness=zeros(N,2);
V=initialization(N,dim,ub,lb);
position_history=zeros(N,max_iter,dim);
for iter=1:max_iter


    c1 = 2*exp(-(4*iter/max_iter)^2); % Eq. (3.2) in the paper


    for i=1:N %Calculate all the objective values first
        Salps_fitness(i,:)=ObjectiveFunction(Salps_X(:,i)');
        if dominates(Salps_fitness(i,:),Food_fitness)
            Food_fitness=Salps_fitness(i,:);
            Food_position=Salps_X(:,i);
        end
    end


    [Archive_X, Archive_F, Archive_member_no]=UpdateArchive(Archive_X, Archive_F, Salps_X, Salps_fitness, Archive_member_no);


    if Archive_member_no>ArchiveMaxSize
        Archive_mem_ranks=RankingProcess(Archive_F, ArchiveMaxSize, obj_no);
        [Archive_X, Archive_F, Archive_mem_ranks, Archive_member_no]=HandleFullArchive(Archive_X, Archive_F, Archive_member_no, Archive_mem_ranks, ArchiveMaxSize);
    else
        Archive_mem_ranks=RankingProcess(Archive_F, ArchiveMaxSize, obj_no);
    end


    Archive_mem_ranks=RankingProcess(Archive_F, ArchiveMaxSize, obj_no);
    % Archive_mem_ranks
    % Chose the archive member in the least population area as food`
    % to improve coverage
    index=RouletteWheelSelection(1./Archive_mem_ranks);
    if index==-1
        index=1;
    end
    Food_fitness=Archive_F(index,:);
    Food_position=Archive_X(index,:)';


    for i=1:N


        index=0;
        neighbours_no=0;


        if i<=N/2
            for j=1:1:dim
                c2=rand();
                c3=rand();
                 % Eq. (3.1) in the paper 
                if c3<0.5
                    Salps_X(j,i)=Food_position(j)+c1*((ub(j)-lb(j))*c2+lb(j));
                else
                    Salps_X(j,i)=Food_position(j)-c1*((ub(j)-lb(j))*c2+lb(j));
                end
            end
        elseif i>N/2 && i<N+1


            point1=Salps_X(:,i-1);
            point2=Salps_X(:,i);


            Salps_X(:,i)=(point2+point1)/(2); % Eq. (3.4) in the paper
        end


        Flag4ub=Salps_X(:,i)>ub';
        Flag4lb=Salps_X(:,i)<lb';
        Salps_X(:,i)=(Salps_X(:,i).*(~(Flag4ub+Flag4lb)))+ub'.*Flag4ub+lb'.*Flag4lb;


    end


    disp(['At the iteration ', num2str(iter), ' there are ', num2str(Archive_member_no), ' non-dominated solutions in the archive']);
end
figure
Draw_ZDT1();
hold on
plot(Archive_F(:,1),Archive_F(:,2),'ro','MarkerSize',8,'markerfacecolor','k');
legend('True PF','Obtained PF');
title('MSSA');

免费完整代码获取，后台回复关键词：

多目标02