一个理想滤波器应该是在通频带内具有均匀且稳定的增益，对信号的其余频带则具有无穷大的衰减。然后，各种实际的频率响应曲线从阻带或从通带到阻带总有一个逐渐过渡的过程，距离理想情况有一定距离，不像其那样跳跃变化，因此只能让所有设计的滤波器的幅频特性去逼近理想滤波器。

各种不同功能的滤波器频率特性如图1所示：

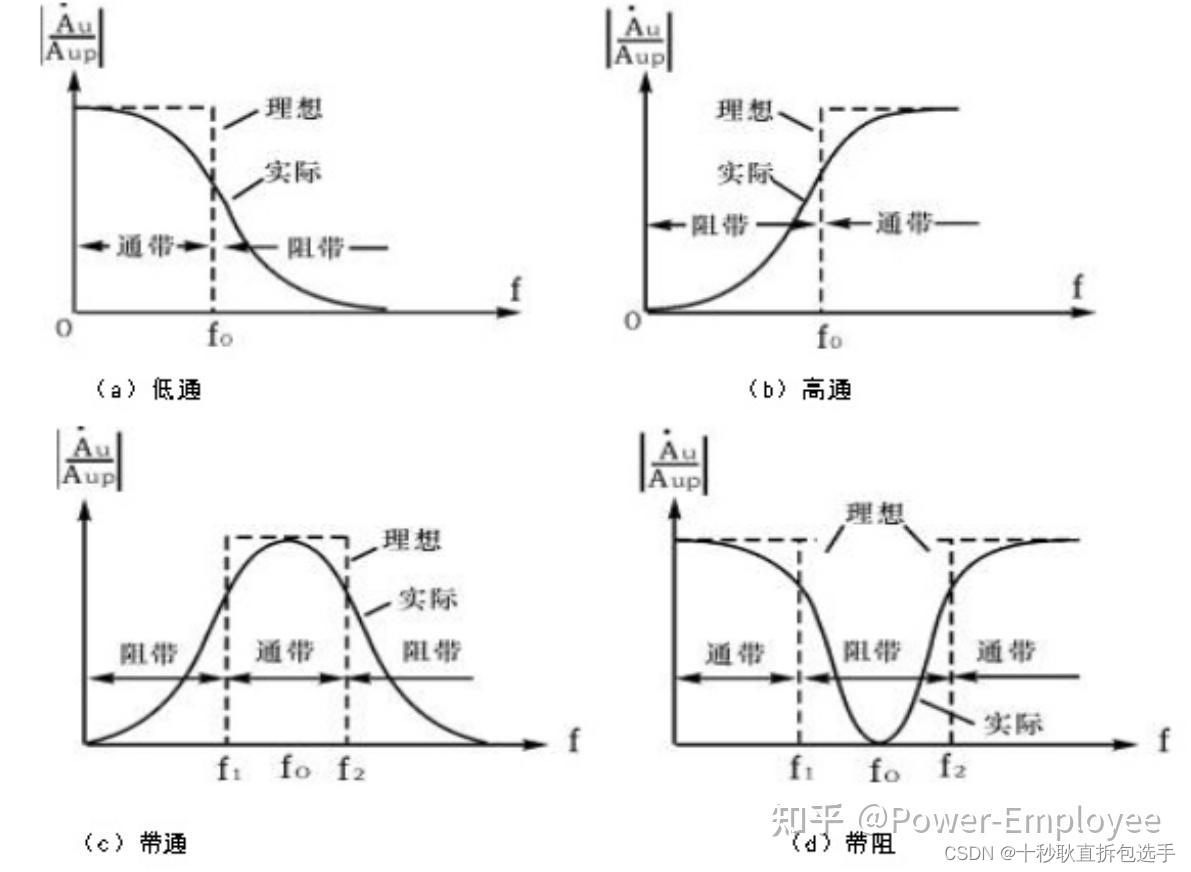
图1-四种常见滤波器幅频示意图

图中通带是指能够通过的信号频带，阻带则是指被抑制或衰减的信号频带，两者分界点的频率分别为f1和f2,称为截止频率或转折频率，f0为中心频率，Aup为通带电压的放大倍数，这四种滤波器之间彼此联系，低通滤波器（LPF)与高通滤波器（HPF)互为对偶关心。当低通滤波器的通带截止频率高于高通滤波器的通带截止频率时，将两者串联就能够成为带通滤波器（BPF)，若两者并联，便构成带阻滤波器(BEF)。

滤波器的三大关键参数：

(1）通带增益a0：滤波器通带内的电压放大倍数。

(2)特征角频率和特征频率fn：它只与滤波用的电阻和电容元件的参数有关，通常对于带通(带阻）滤波器，称为带通(带阻）滤波器的中心角频率或中心频率f0，是通带(阻带）内电压增益最大(最小）点的频率。

(3)截止角频率和截止频率f0：它是电压增益下降到(即)时所对应的角频率。必须注意不一定等于。带通和带阻滤波器有两个。

(4）通带(阻带)宽度bw：它是带通(带阻)滤波器的两个截止频率之差值。

5)等效品质因数q：对低通和高通滤波器而言,q值等于滤波器电路电压增益（截止频率对应处的增益）模|��|与通带增益的模 |���| 之比.常见的品质因数可调的二阶低通滤波器有压控电压源二阶低通滤波器，其品质因数 �=13−��� 式中，Aup为通带增益，对于低通滤波而言，Aup为频率为零时增益。因此，调节通带增益，就可以调节品质因数，对于二阶高通滤波器，其品质因数 �=13−��� ；对带通(带阻）滤波器而言,q值等于中心角频率与通带(阻带）宽度bw之比。Q对于带通滤波有特殊意义，它是滤波器的选择性，即Q= �=�0�2−�1 ，可以证明,谐振频率(f0)为f1和f2的几何平均值，这就意味着，f0在对数尺度上将出现在f1和f2二者的中点，即 �0=�1�2 。请注意，可以证明谐振频率(f0)为f1和f2的几何平均值，这就意味着，f0在对数尺度上将出现在f1和f2二者的中点。