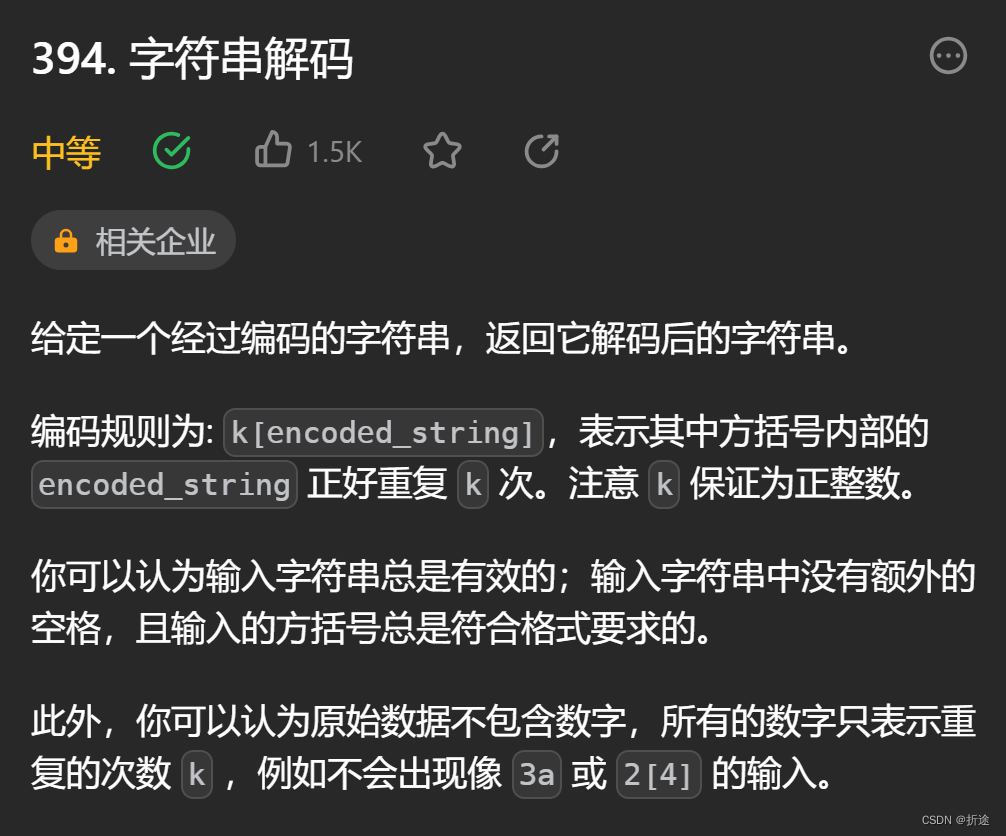
题目：

示例：

分析：

给我们字符串，让我们解码，那么该怎么解码呢，被括号【】包裹起来的字符串需要扩展成括号左边第一个数字（可能不止一位数）倍，例如 3【a】需要变成 aaa。

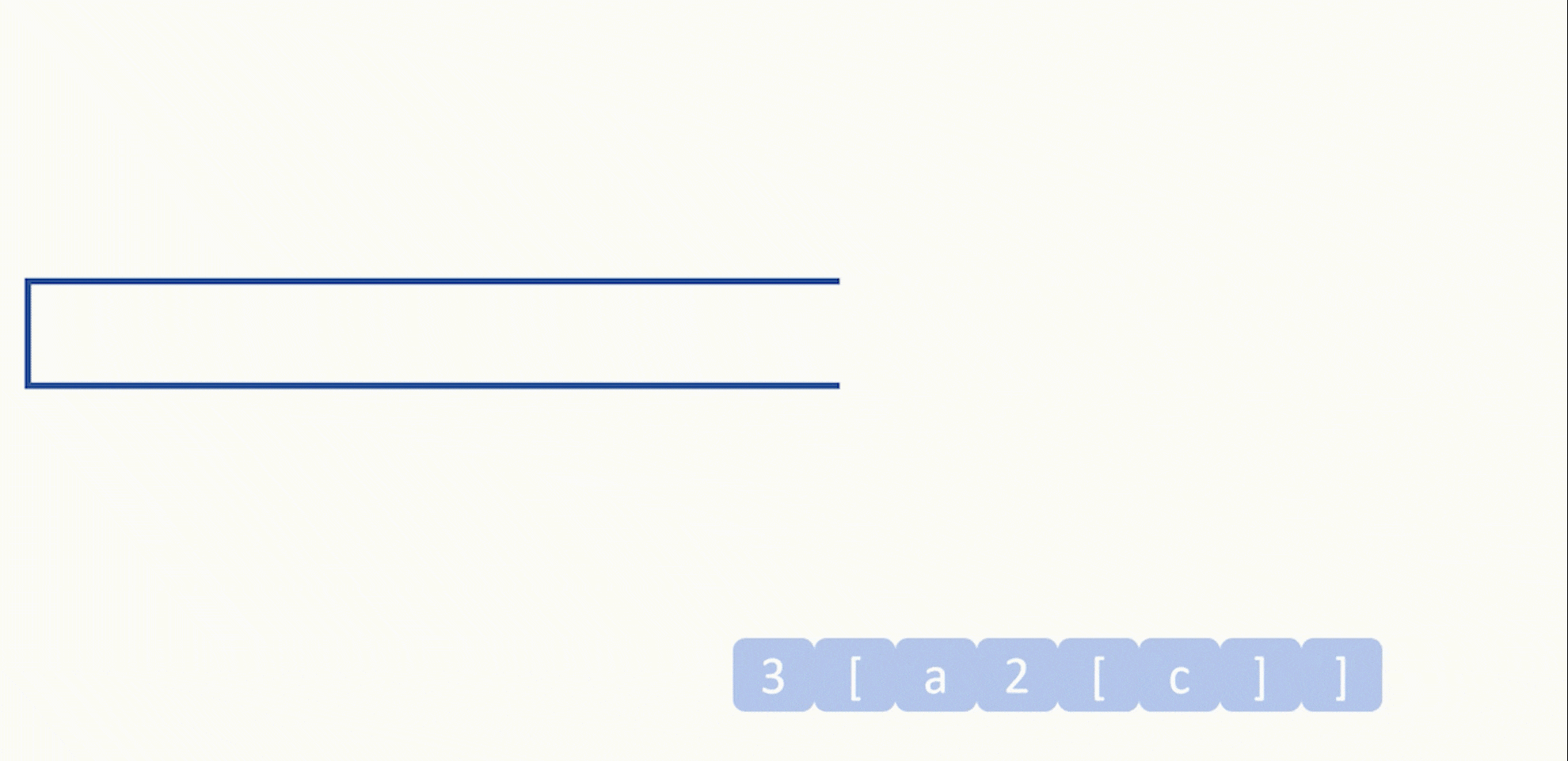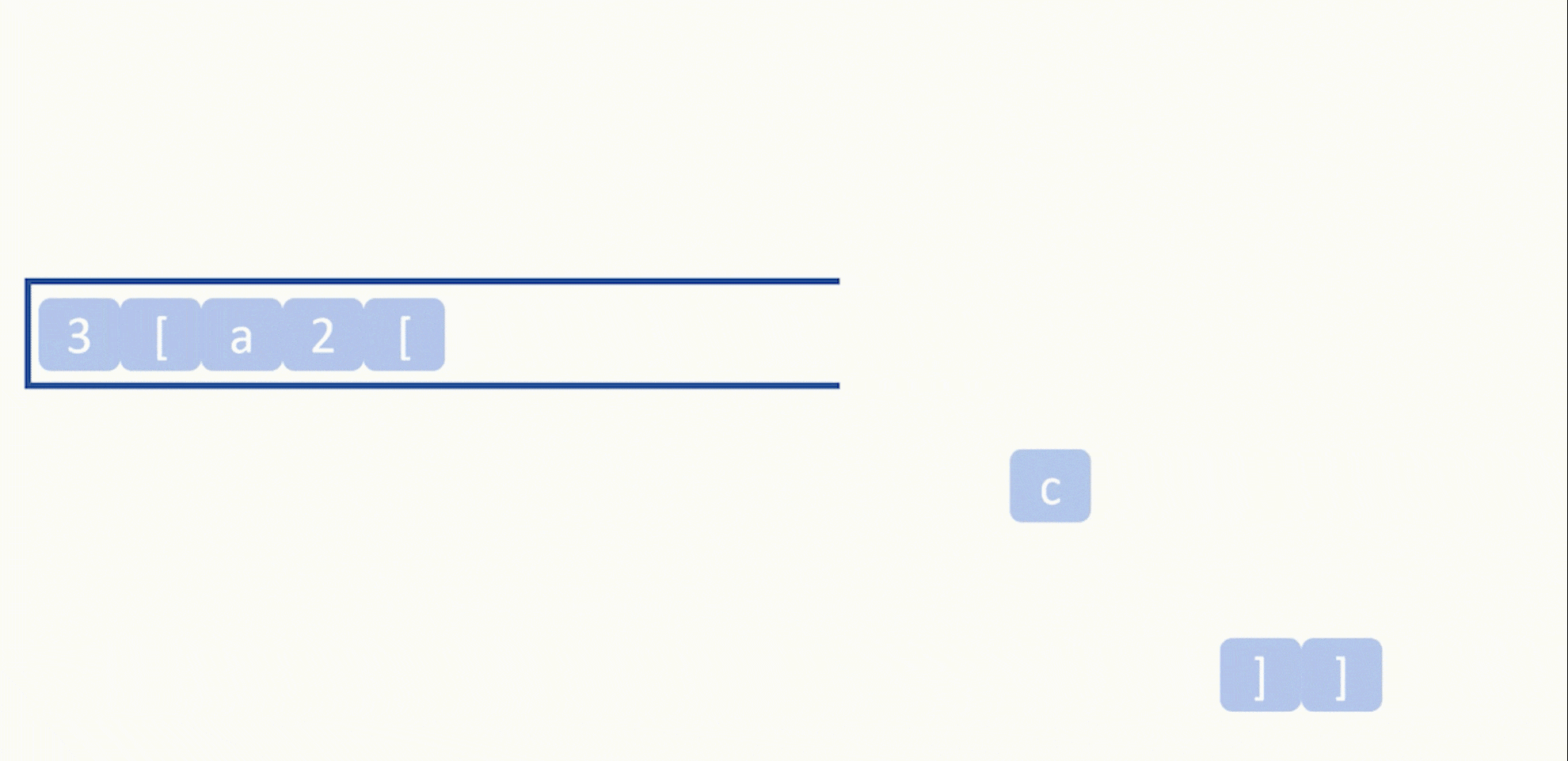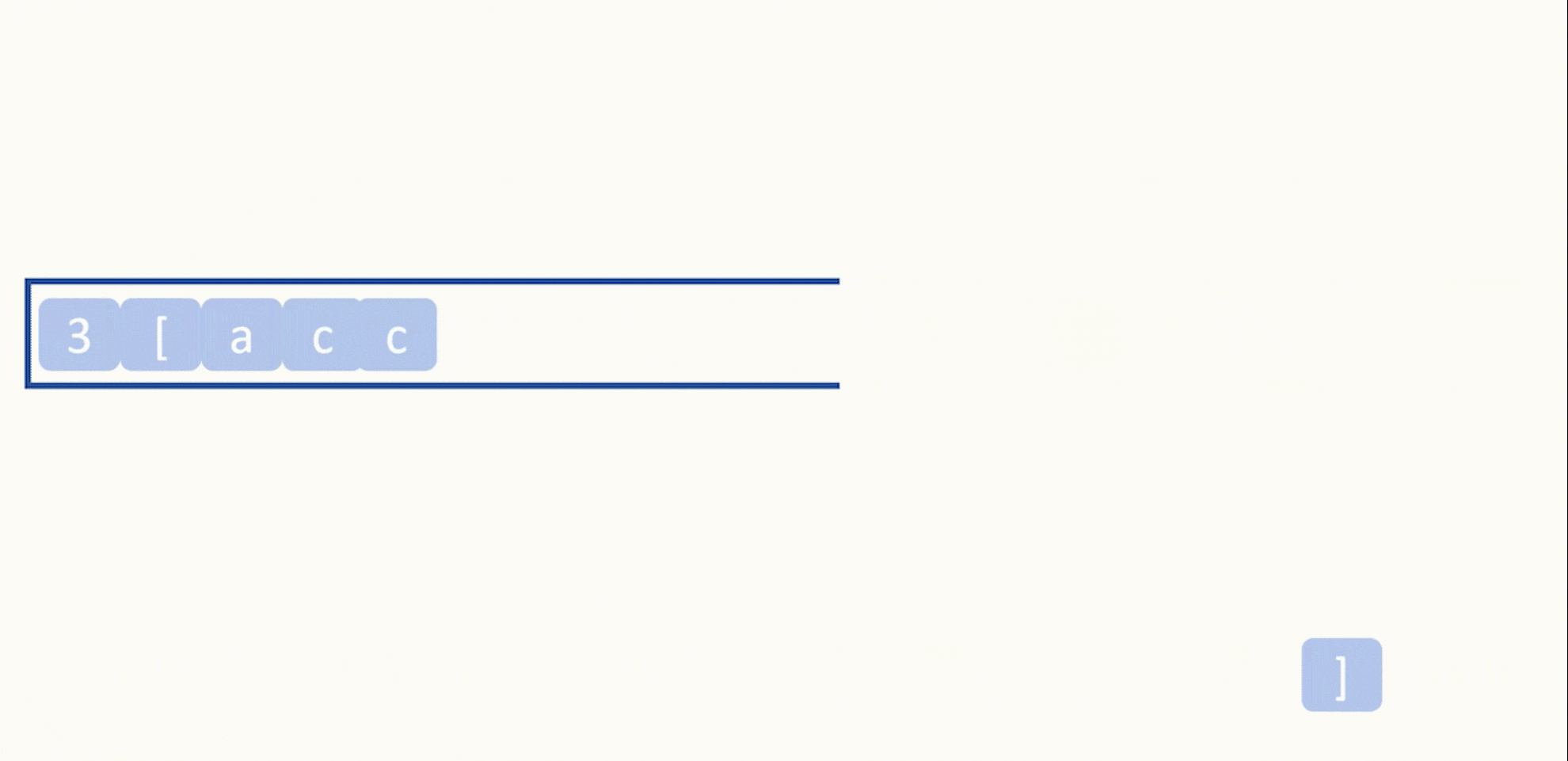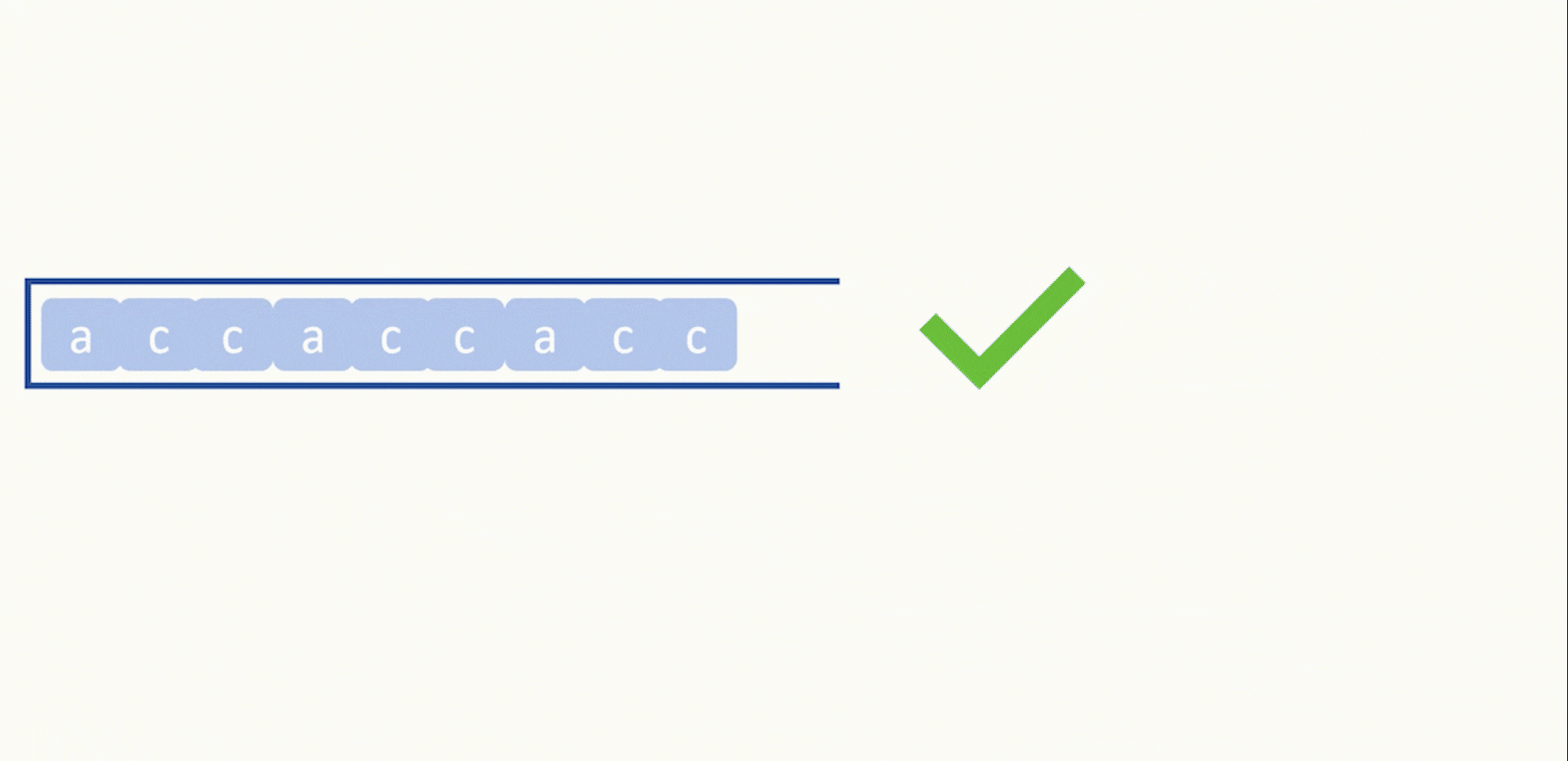
我们可以发现，如果发现括号嵌套（括号里还有括号），那么我们应该先算最里面的括号，这样解码才是正确的，换一个说法，我们应该先解码左括号更后面出现的，这就算是先进后出，后进先出了，不难想到可以利用栈的特性来做。

先遍历字符串，我们直接将非右括号的字符全部入栈，直到遇到了右括号才开始解码。

遇到右括号之后一直取栈顶元素直到碰到左括号，这样我们就算是把需要扩展的字符串拿到手了。

接着我们需要拿到扩展字符串的次数，因为题目说扩展次数最多是300次，因此我们不能只取左括号左边的一位数字，而需要一直取数直到栈空或是碰到了非数字。

然后得到扩展的字符串和扩展次数以后，将扩展后的字符串再依次入栈。

如此循环，即可得到解码后的字符串了。

代码+运行结果：

class Solution {
public:
    string decodeString(string s) {
        vector<char>Stack;
        for(char &c:s){
            if(c==']'){ //如果碰到右括号,那么开始寻找是哪些字符串需要解码
                string tempstr="";
                while((*(Stack.end()-1))!='['){ //获取括号内的字符串
                    tempstr=(*(Stack.end()-1))+tempstr; 
                    Stack.pop_back();
                }
                Stack.pop_back();   //将左括号[弹出
                int times=0;int beishu=0;   //获取重复次数
                while(!Stack.empty()&&isdigit(*(Stack.end()-1))){
                    times+=(pow(10,beishu++)*(static_cast<int>((*(Stack.end()-1)-'0'))));
                    Stack.pop_back();
                }  
                //开始解码字符串(重复字符串)
                for(int i=0;i<times;i++){
                    for(char &t:tempstr){
                        Stack.push_back(t);
                    }
                }
            }else{  //除了右括号以外的其他符号都入栈
                Stack.push_back(c);
            }
        }
        string res="";
        //拼接最终结果
        for(char &c:Stack) res+=c;
        return res;
    }
};