等高线图的含义
等高线图(Contour plot)是一种二维图形展示方式,用于表示函数在二维平面上的等高线。等高线图的每条等高线代表函数在该高度上的取值相同的点的集合。
等高线图的绘制方法
在matplotlib中,可以使用contour()函数绘制等高线图。
参数解释:
X:二维数组,表示 x 坐标的网格点。
Y:二维数组,表示 y 坐标的网格点。
Z:二维数组,表示函数在对应网格点的取值。
levels:可选参数,表示要绘制的等高线的高度值。默认为 None,表示自动生成等高线。
kwargs:其他可选参数,用于设置等高线的样式和属性。
以下是一些常用的kwargs参数:
colors:设置等高线的颜色。可以是单个颜色字符串,也可以是颜色字符串列表。默认为 None,表示使用默认颜色。
cmap:设置等高线的颜色映射。可以是 matplotlib 的 colormap 对象或 colormap 名称。默认为 None,表示使用默认颜色映射。
linewidths:设置等高线的线宽。可以是单个线宽值,也可以是线宽值列表。默认为 None,表示使用默认线宽。
alpha:设置等高线的透明度。取值范围为 0 到 1,默认为 1,表示完全不透明。
linestyles:设置等高线的线型。可以是单个线型字符串,也可以是线型字符串列表。默认为 None,表示使用默认线型。
extend:设置颜色映射的扩展。可以是 ‘neither’、‘both’、‘min’ 或 ‘max’。默认为 ‘neither’,表示不扩展颜色映射。
locator:设置等高线标签的位置定位器。可以是 matplotlib.ticker.Locator 对象,也可以是 locator 名称字符串。默认为 None,表示使用默认定位器。
等高线图在量化交易中的应用
在下面的案例中,使用等高线图绘制中国平安2023年3月的开盘价、收盘价、最高价、最低价的等高线图。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
# 设置为默认字体
plt.rcParams['font.family'] = 'SimHei'
# 显示负数
plt.rcParams['axes.unicode_minus'] = False
# 导入数据
df = pd.read_excel("2023年一季度A股日线行情.xlsx")
# 将日期列转化为日期格式
df["trade_date"] = df["trade_date"].astype("str").apply(lambda x:x[:4]+"-"+x[4:6]+"-"+x[6:])
# 将日期列转换为日期类型,并设置为索引列
df['trade_date'] = pd.to_datetime(df['trade_date'])
df.set_index('trade_date', inplace=True)
# 筛选2023年3月的行情数据
start_date = '2023-03-01'
end_date = '2023-03-31'
df = df.loc[start_date:end_date]
# 筛选中国平安的3月股票交易数据
stock = df[df['ts_code']=='000001.SZ']
# 生成一个列表,再转置成4*23矩阵(开盘价、收盘价、最高价、最低价四列,23个交易日)
price_data = []
price_data.append(stock['open'].tolist())
price_data.append(stock['close'].tolist())
price_data.append(stock['high'].tolist())
price_data.append(stock['low'].tolist())
price_data = np.array(price_data)
# 生成坐标
x = np.arange(1, 24) # 日期
y = np.arange(4) # 价格类型
X, Y = np.meshgrid(x, y)
# 设置图形大小
plt.figure(figsize=(10, 10))
# 绘制等高线图
plt.contourf(X, Y, price_data, cmap='coolwarm')
# 添加颜色条
plt.colorbar()
# 设置x轴刻度
x_labels = [str(i)[6:10] for i in stock.index]
plt.xticks(x, x_labels)
# 设置y轴刻度
plt.yticks(y, ['High', 'Low', 'Open', 'Close'])
# 设置x轴标签
plt.xlabel('Date')
# 设置y轴标签
plt.ylabel('Price Type')
# 设置图标题
plt.title('Stock Price Fluctuation')
# 显示图形
plt.show()
最终效果图如下:
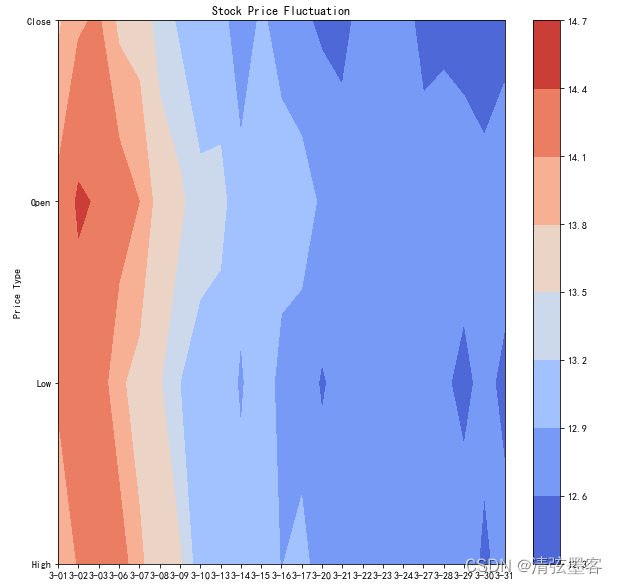
从上图中我们可以发现,3月份平安银行的日均线都比较高,但是从3月9日之后,日均价格一直下探,所以在此期间不宜购入股票。



![[保研/考研机试] KY183 素数 北京航空航天大学复试上机题 C++实现](https://img-blog.csdnimg.cn/img_convert/35f839fabf443605d1a50db036c3d7bc.png)