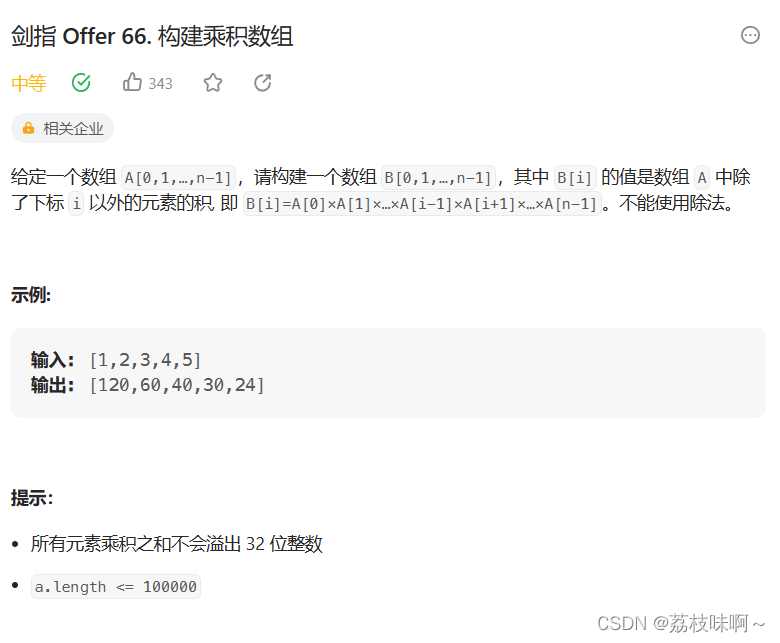
我一开始的想法就是，先把所有数的乘积求出来，然后遍历数组，用这个积除以它，就是除了这个数外所有数的乘积。但是题目明确给了不能用除法，所以可不可以用位运算来实现除法呢。

class Solution {
    public int[] constructArr(int[] a) {
        long b = 1L;int zeroNum =0;
        for(int i =0;i<a.length;i++){
            int bol=0;
             if(a[i] == 0){
                 zeroNum++;
                 continue;
             }else{
                b=b*a[i];
             }
        }
        int[] res = new int[a.length];
        for(int i=0;i<a.length;i++){
            if(zeroNum<=1){
               if(a[i]==0){
                res[i]=(int)b;
            }else{
                if(zeroNum==1){
                    res[i] = 0;
                }else{
                     res[i] = divide((int)b, a[i]);
                }
            }
            }else{
                res[i] = 0;
            }    
        }
        return res;
    }
      public int divide(int a, int b) {
        if (a == 0)
            return 0;
        if (a == b)
            return 1;
        if (a == Integer.MIN_VALUE && b == -1)
            return Integer.MAX_VALUE;
        boolean f = (a ^ b) < 0;
        long a1 = Math.abs((long)a);
        long b1 = Math.abs((long)b);
        int res = 0;
        for (int i = 31; i >= 0; i--) {
            if ((a1 >> i) >= b1) {
                a1 -= (b1 << i);
                res += (1 << i);
            }
        }
        return f ? -res : res;
    }
}

divide方法就是利用位运算实现除法，a是被除数，b是除数，如果被除数是0直接返回0，如果被除数等于除数直接返回1，如果被除数是最大整型，除数是-1为防止溢出，返回最大整型，f是ab异或的结果，判断他们的符号是否相同，然后用a1b1取他们得得绝对值，通过不断将被除数 a1 减去 b1 的左移结果，同时记录每次减去的次数（左移的位数），即每次迭代中，检查 (a1 >> i) >= b1，如果成立，则将 a1 减去 b1 << i，并将结果累加到 res 中，即 res += (1 << i)。返回最终结果 res，如果之前判断的 f 为真，说明结果应该为负数，所以返回 -res。

然后需要注意的就是数组中0的个数，如果0的个数大于1，那么无论放弃哪个数，其余数的乘积都是0。如果0的个数是一个，那么寻找所有数的乘积的时候需要跳过这个0，其他元素的对应位置的积都返回0，0对应位置上的积返回所有数的积。

题解用的左右乘积列表，就数组中除了这个数外的所有数的乘积=这个数左边所有数的乘积*这个数右边所有数的乘积。所以可以创建两个数组，一个是左乘积数组L，一个是右乘积数组R，L[i]表示a[i]左边所有数的乘积，R[i]同理，L[0]=1，L[i]=L[i-1]*a[i-1]；同理R[a.length-1]=1,R[i] = R[i+1]*a[i+1];这样L数组和R数组就创建完了，最后只要R[i]*L[i]就是除a[i]外所有数的积了。

class Solution {
    public int[] productExceptSelf(int[] a) {
        int length = a.length;

        // L 和 R 分别表示左右两侧的乘积列表
        int[] L = new int[length];
        int[] R = new int[length];

        int[] answer = new int[length];

        // L[i] 为索引 i 左侧所有元素的乘积
        // 对于索引为 '0' 的元素，因为左侧没有元素，所以 L[0] = 1
        L[0] = 1;
        for (int i = 1; i < length; i++) {
            L[i] = a[i - 1] * L[i - 1];
        }

        // R[i] 为索引 i 右侧所有元素的乘积
        // 对于索引为 'length-1' 的元素，因为右侧没有元素，所以 R[length-1] = 1
        R[length - 1] = 1;
        for (int i = length - 2; i >= 0; i--) {
            R[i] = a[i + 1] * R[i + 1];
        }

        // 对于索引 i，除 a[i] 之外其余各元素的乘积就是左侧所有元素的乘积乘以右侧所有元素的乘积
        for (int i = 0; i < length; i++) {
            answer[i] = L[i] * R[i];
        }

        return answer;
    }
}