题目链接
Leetcode.1289 下降路径最小和 II
rating : 1697
题目描述
给你一个 n x n 整数矩阵
g
r
i
d
grid
grid ,请你返回 非零偏移下降路径 数字和的最小值。
非零偏移下降路径 定义为:从 g r i d grid grid 数组中的每一行选择一个数字,且按顺序选出来的数字中,相邻数字不在原数组的同一列。
示例 1:
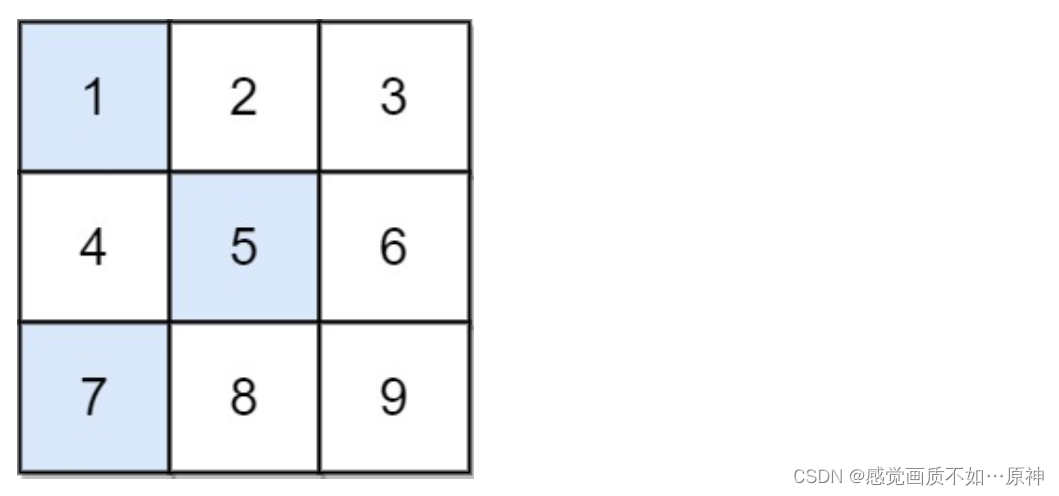
输入:grid = [[1,2,3],[4,5,6],[7,8,9]]
输出:13
解释:
所有非零偏移下降路径包括:
[1,5,9], [1,5,7], [1,6,7], [1,6,8],
[2,4,8], [2,4,9], [2,6,7], [2,6,8],
[3,4,8], [3,4,9], [3,5,7], [3,5,9]
下降路径中数字和最小的是 [1,5,7] ,所以答案是 13 。
示例 2:
输入:grid = [[7]]
输出:7
提示:
- n = g r i d . l e n g t h = g r i d [ i ] . l e n g t h n = grid.length = grid[i].length n=grid.length=grid[i].length
- 1 ≤ n ≤ 200 1 \leq n \leq 200 1≤n≤200
- − 99 ≤ g r i d [ i ] [ j ] ≤ 99 -99 \leq grid[i][j] \leq 99 −99≤grid[i][j]≤99
解法一:记忆化搜索
我们定义 f ( i , j ) f(i,j) f(i,j)为 从位置 ( i , j ) (i,j) (i,j) 到第一行的 非偏移路径的 最小值。
按照定义,最终要返回的答案就是
m i n { f ( n − 1 , j ) } ( 0 ≤ j < n ) min\{ f(n - 1,j)\} (0 \leq j < n) min{f(n−1,j)}(0≤j<n)
由于相邻的两行不能选择同一列。
所以状态转移方程为:
f ( i , j ) = m i n { f ( i − 1 , k ) } + g r i d [ i ] [ j ] ( 0 ≤ k < n , k ≠ j ) f(i,j) = min\{ f(i - 1,k)\} + grid[i][j] \qquad (0 \leq k < n,k\neq j) f(i,j)=min{f(i−1,k)}+grid[i][j](0≤k<n,k=j)
注意:
- 如果此时 i = 0 i = 0 i=0,即来到了第一排,此时直接返回 g r i d [ i ] [ j ] grid[i][j] grid[i][j] 即可。
- 如果此时 i < 0 i < 0 i<0,说明已经超出了边界,由于我们是要求最小值,所以直接返回一个较大的数,这里我返回 1 0 9 10^9 109。
时间复杂度: O ( n 3 ) O(n^3) O(n3)
C++代码:
class Solution {
public:
int minFallingPathSum(vector<vector<int>>& grid) {
int n = grid.size();
vector<vector<int>> memo(n,vector<int>(n,-1));
function<int(int,int)> dfs = [&](int i,int j) ->int{
if(i < 0) return 1e9;
if(i == 0) return grid[i][j];
int& ans = memo[i][j];
if(ans != -1) return ans;
int t = 1e9;
for(int k = 0;k < n;k++){
if(k != j){
t = min(t , dfs(i - 1,k) + grid[i][j]);
}
}
ans = t;
return ans;
};
int ans = 1e9;
for(int i = 0;i < n;i++){
ans = min(ans , dfs(n - 1,i));
}
return ans;
}
};
解法二:动态规划
我们定义 f ( i , j ) f(i,j) f(i,j) 为从第一排开始终点是 ( i , j ) (i,j) (i,j) 的非偏移路径的最小值。
f ( i , j ) = { g r i d [ i ] [ j ] ( i = 0 ) m i n { f [ i − 1 ] [ k ] } + g r i d [ i ] [ j ] ( 0 ≤ k ≤ n , k ≠ j ) \begin{equation} f(i,j) = \left\{ \begin{aligned} %\nonumber &grid[i][j] &(i = 0)\\ &min\{ f[i - 1][k]\} + grid[i][j] \qquad &(0\leq k \leq n,k \neq j)\\ \end{aligned} \right. \end{equation} f(i,j)={grid[i][j]min{f[i−1][k]}+grid[i][j](i=0)(0≤k≤n,k=j)
时间复杂度: O ( n 3 ) O(n^3) O(n3)
C++代码:
class Solution {
public:
int minFallingPathSum(vector<vector<int>>& grid) {
int n = grid.size();
int f[n][n];
memset(f,0,sizeof f);
for(int j = 0;j < n;j++) f[0][j] = grid[0][j];
for(int i = 1;i < n;i++){
for(int j = 0;j < n;j++){
int t = 1e9;
for(int k = 0;k < n;k++){
if(k == j) continue;
t = min(t , f[i - 1][k] + grid[i][j]);
}
f[i][j] = t;
}
}
int ans = 1e9;
for(int j = 0;j < n;j++) ans = min(ans , f[n - 1][j]);
return ans;
}
};
解法三:动态规划 + 优化
我们发现,我们计算 f ( i , j ) f(i,j) f(i,j) 的时候,只需要用到 m i n { f [ i − 1 ] [ k ] } min\{ f[i - 1][k]\} min{f[i−1][k]} 这个状态。如果上一层最小的路径和,正好在位置 j j j 上,那么我们只需要取上一层倒数第二小的状态。
所以,我们只需要用到上一层最小的状态 m i mi mi ,倒数第二小的状态 s e c o n d _ m i second\_mi second_mi,以及上一层最小状态所在的位置 i d x idx idx。
f ( i , j ) = { g r i d [ i ] [ j ] ( i = 0 ) m i + g r i d [ i ] [ j ] ( k ≠ j ) s e c o n d _ m i + g r i d [ i ] [ j ] ( k = j ) \begin{equation} f(i,j) = \left\{ \begin{aligned} %\nonumber &grid[i][j] &(i = 0)\\ &mi+ grid[i][j] \qquad &(k \neq j)\\ &second\_mi+ grid[i][j] \qquad &(k = j)\\ \end{aligned} \right. \end{equation} f(i,j)=⎩ ⎨ ⎧grid[i][j]mi+grid[i][j]second_mi+grid[i][j](i=0)(k=j)(k=j)
时间复杂度: O ( n 2 ) O(n^2) O(n2)
C++代码:
class Solution {
public:
int minFallingPathSum(vector<vector<int>>& grid) {
int n = grid.size();
int mi = 0 , second_mi = 0 , idx = -1;
for(int i = 0;i < n;i++){
//本层的状态
int cur_min = 1e9 , cur_second_mi = 1e9 , cur_idx = -1;
for(int j = 0;j < n;j++){
int sum = (j != idx ? mi : second_mi) + grid[i][j];
//本来是 cur_second_mi < cur_mi
//现在出现了 sum , sum < cur_mi < cur_second_mi
//也就是 cur_second_mi 要更新为 cur_mi
//cur_mi 要更新为 sum
//还要更新最小状态的下标 j
if(sum < cur_min){
cur_second_mi = cur_min;
cur_min = sum;
cur_idx = j;
}
else if(sum < cur_second_mi) cur_second_mi = sum;
}
//更新状态
mi = cur_min;
idx = cur_idx;
second_mi = cur_second_mi;
}
return mi;
}
};