1.案例背景

1.1 SOM神经网络概述

自组织特征映射网络(Self - Organizing Feature Map,SOM)也称Kohonen网络,它是由荷兰学者Teuvo Kohonen于1981年提出的。该网络是一个由全连接的神经元阵列组成的无教师、自组织、自学习网络。Kohonen认为,处于空间中不同区域的神经元有着不同的分工，当一个神经网络接受外界输入模式时,将会分为不同的反应区域,各区域对输入模式具有不同的响应特性。
自组织特征映射神经网络根据输入空间中输人向量的分组进行学习和分类,其与第21章案例中的自组织网络(竞争层网络)的区别在于:在SOM网络中,竞争层中的神经元会尝试识别输入空间临近该神经元的部分,也就是说,SOM神经网络既可以学习训练数据输入向量的分布特征,也可以学习训练数据输人向量的拓扑结构。与SOM拓扑排序特征有关的重要特点是每个神经元与其近邻的神经元也是相关联的。在权值更新过程中,不仅获胜神经元的权值向量得到更新,而且其近邻神经元的权值向量也按照某个“近邻函数”进行更新。这样在开始时移动量很大,权值向量大致地可按它们的最终位置来排序;最后,只移动单个权值向量(微调)。这样就形成了一种特殊的分类法,权值向量按照这样一种方式变为有序,即它们在某个“弹性”网格上代表着输入向量。如果网格的某个位置有变化,那么这种变化将影响到此神经元的近邻。但是,离该神经元越远,这种影响就越小。因此,在竞争层的神经元位置演变的过程中,每个区域代表一类输入向量。换句话说,要用若干个权值向量来表示一个数据集(输入向量),每个权值向量表示某一类输入向量的均值。

通过训练,可以建立起这样一种布局,它使得每个权值向量都位于输入向量聚类的中心。一旦 SOM完成训练,就可以用于对训练数据或其他数据进行聚类。

1.2 SOM神经网络结构

典型的SOM网络结构如图22-1所示,由输入层和竞争层(有些书上也称为映射层)组成。输人层神经元个数为m,竞争层是由a×b个神经元组成的二维平面阵列,输入层与竞争层各神经元之间实现全连接。

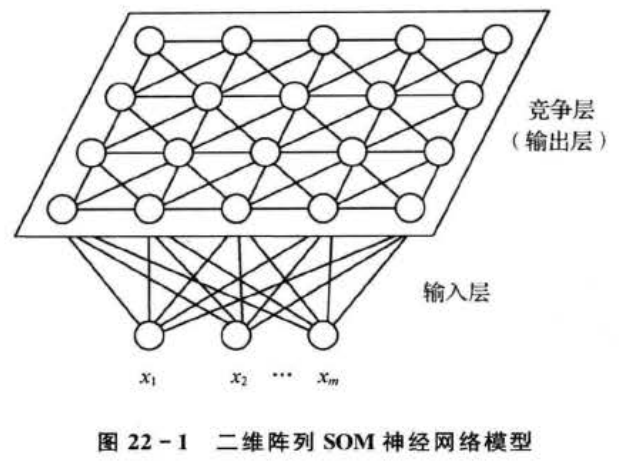
SOM网络的一个典型特征就是可以在一维或者二维的处理单元阵列上,形成输人信号的特征拓扑分布,因此SOM网络具有抽取输入信号模式特征的能力。SOM网络一般只包含有一维阵列和二维阵列,但也可以推广到多维处理单元阵列中去。SOM网络模型由以下4个部分组成。
①处理单元阵列。用于接收事件输入,并且形成对这些信号的“判别函数”。

②比较选择机制。用于比较“判别函数”,并选择一个具有最大函数输出值的处理单元。

③局部互联作用。用于同时激励被选择的处理单元及其最邻近的处理单元。
④自适应过程。用于修正被激励的处理单元的参数,以增加其对应于特定输人“判别函数”的输出值。

1.3SOM 神经网络学习算法

Kohonen自组织特征映射算法能够自动找出输入数据之间的类似度,将相似的输人在网络上就近配置,因此是一种可以构成对输入数据有选择地给予反应的网络。Kohonen 的自组织特征映射的学习算法步骤如下:

1.4柴油机故障诊断概述

随着科学与生产技术的发展,现代设备大多数集机电液于一体,结构越来越复杂,自动化程度越来越高。在工作过程中,故障发生的概率相对提高,出现故障后不仅会造成经济损失，甚至会导致整个设备遭受灾难性的毁坏。柴油机由于其本身的结构异常复杂,加之系统的输入输出不明显,难以用比较完备准确的模型对其机构、功能以及状态等进行有效的描述,因而给故障诊断带来了很大麻烦。近年来,随着模式识别和神经网络理论的引入,柴油机故障诊断技术有了较快发展。神经网络技术的出现,为故障诊断问题提供了一种新的解决途径,特别是对于柴油机这类复杂系统。神经网络的输入输出非线性映射特性,信息的分布存储,并行处理和全局集体应用,特别是其高度的自组织和自学习能力,使其成为故障诊断的一种有效方法和手段。

对于燃油压力波形(见图22-2)来说,最大压力(P)、次最大压力(Pz)、波形幅度(P3)、上升沿宽度(P4)、波形宽度(P.)、最大余波的宽度(P6)、波形的面积(Pz)、起喷压力(P.)等特征最能体现柴油机运行的状况。

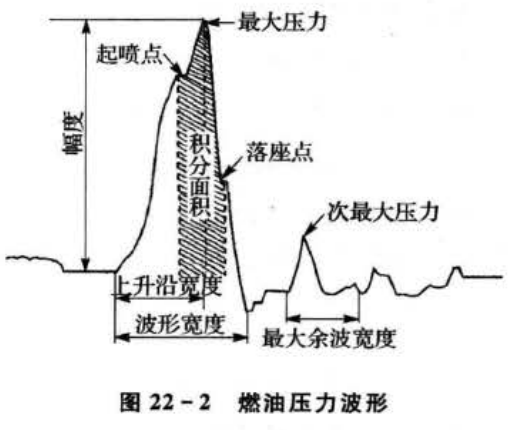
燃油系统常见的故障有供油量不足、针阀门卡死致油孔阻塞、针阀泄露、出油阀失效等几种故障。本例里诊断的故障也是基于上述故障,主要有100%供油量(T1)、75%供油量(T2)、25%供油量(T3)、怠速油量(T4)、针阀卡死(小油量T5)、针阀卡死(标定油量T6)、针阀泄露(T7)、出油阀失效(T8)8种故障。

2 模型建立

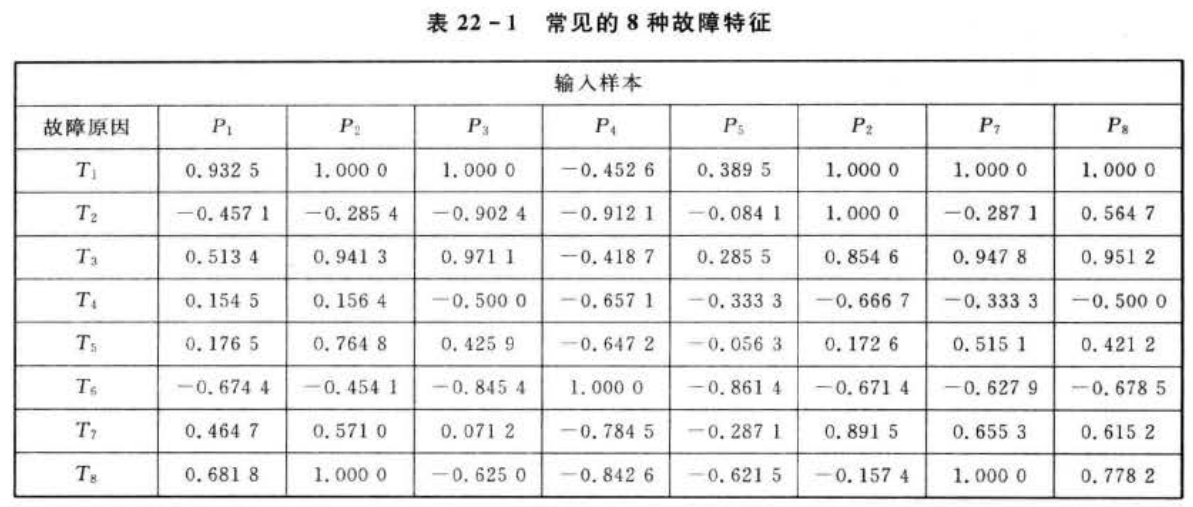
本案例中给出了一个含有8个故障样本的数据集。每个故障样本中有8个特征,分别是前面提过的:最大压力(P1)、次最大压力(P2)、波形幅度(P3)、上升沿宽度(P4)、波形宽度(P5)、最大余波的宽度(P6)、波形的面积(P7),起喷压力(P8),使用SOM网络进行故障诊断。故障样本如表22-1所列(数据已归一化)。

应用 SOM神经网络诊断柴油机故障的步骤如下:

①选取标准故障样本;
        ②对每一种标准故障样本进行学习,学习结束后,对具有最大输出的神经元标以该故障的记号;
        ③将待检样本输人到 SOM神经网络中;
        ④若输出神经元在输出层的位置与某标准故障样本的位置相同,说明待检样本发生了相应的故障;若输出神经元在输出层的位置介于很多标准故障之间,说明这几种标准故障都有可能发生,且各故障的程度由该位置与相应标准故障样本位置的欧氏距离确定。

3 MATLAB 实现

代码中使用到的相关函数介绍如下。

3.1 SOM的创建函数

newsom()函数用于创建一个自组织特征映射。其调用格式为:

net=newsom(PR,[d1,d1,...],tfcn,dfcd,olr,osteps,tlr,tns)

其中，PR为R个输入元素的最大值和最小值的设定值,为R×2维矩阵;di为第i层的维数，默认值为[5,8]; tfcn为拓扑函数(即结构函数)，默认值为"hextop"; dfcn为距离函数﹐默认值为"linkdist" ;olr为分类阶段学习速率,默认值为0.9;osteps为分类阶段学习的步长,默认值为1000;tlr为调谐阶段的学习速率,默认值为0.02;tns为调谐阶段的邻域距离,默认值为1。函数返回一个自组织特征映射。

3.2 SOM 距离函数

(1)boxdist()
该函数为Box距离函数。在给定神经网络竞争层神经元的位置后,可利用该函数计算神经元之间的距离。该函数通常用于结构函数gridtop的神经网络层。其调用格式为:

d=boxdist(pos)

其中， pos 为神经元位置的N×S 维矩阵； d 为函数返回值，神经元距离的S×S 维姐阵。

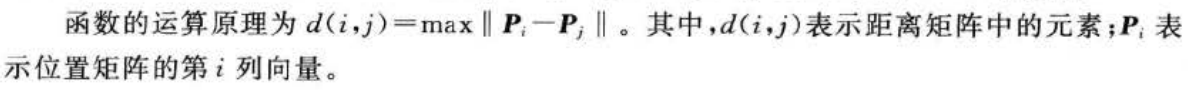
3.3 SOM 结构函数

3.4 完整matlab代码

%% Matlab神经网络43个案例分析

%% 清空环境变量
clc
clear

%% 录入输入数据
% 载入数据
load p;

%转置后符合神经网络的输入格式
P=P';

%% 网络建立和训练
% newsom建立SOM网络。minmax（P）取输入的最大最小值。竞争层为6*6=36个神经元
net=newsom(minmax(P),[6 6]);
plotsom(net.layers{1}.positions)
% 5次训练的步数
a=[10 30 50 100 200 500 1000];
% 随机初始化一个1*10向量。
yc=rands(7,8);
%% 进行训练
% 训练次数为10次
net.trainparam.epochs=a(1);
% 训练网络和查看分类
net=train(net,P);
y=sim(net,P);
yc(1,:)=vec2ind(y);
plotsom(net.IW{1,1},net.layers{1}.distances)

% 训练次数为30次
net.trainparam.epochs=a(2);
% 训练网络和查看分类
net=train(net,P);
y=sim(net,P);
yc(2,:)=vec2ind(y);
plotsom(net.IW{1,1},net.layers{1}.distances)

% 训练次数为50次
net.trainparam.epochs=a(3);
% 训练网络和查看分类
net=train(net,P);
y=sim(net,P);
yc(3,:)=vec2ind(y);
plotsom(net.IW{1,1},net.layers{1}.distances)


% 训练次数为100次
net.trainparam.epochs=a(4);
% 训练网络和查看分类
net=train(net,P);
y=sim(net,P);
yc(4,:)=vec2ind(y);
plotsom(net.IW{1,1},net.layers{1}.distances)


% 训练次数为200次
net.trainparam.epochs=a(5);
% 训练网络和查看分类
net=train(net,P);
y=sim(net,P);
yc(5,:)=vec2ind(y);
plotsom(net.IW{1,1},net.layers{1}.distances)

% 训练次数为500次
net.trainparam.epochs=a(6);
% 训练网络和查看分类
net=train(net,P);
y=sim(net,P);
yc(6,:)=vec2ind(y);
plotsom(net.IW{1,1},net.layers{1}.distances)

% 训练次数为1000次
net.trainparam.epochs=a(7);
% 训练网络和查看分类
net=train(net,P);
y=sim(net,P);
yc(7,:)=vec2ind(y);
plotsom(net.IW{1,1},net.layers{1}.distances)
yc
%% 网络作分类的预测
% 测试样本输入
t=[0.9512 1.0000 0.9458 -0.4215 0.4218 0.9511 0.9645 0.8941]';
% sim( )来做网络仿真
r=sim(net,t);
% 变换函数 将单值向量转变成下标向量。
rr=vec2ind(r)

%% 网络神经元分布情况
% 查看网络拓扑学结构
plotsomtop(net)
% 查看临近神经元直接的距离情况
plotsomnd(net)
% 查看每个神经元的分类情况
plotsomhits(net,P)

运行结果如下：

yc =

     1     5     1     3     1    36     1     1
     1    35     1    36     4    36    13     7
     1    35     1    24    19    36    25     8
     1     6     1    36    28    24     9    25
     1     6    13    34    21    36     9    31
     1    31     3    24    16    34    20     6
     1     6    13    34    20    24     9    31


rr =

     2

聚类的结果如表22-2所列，当训练步数为10时,故障原因1、3分为一类，2、4、6分为一类，5,8分为一类,7单独分为一类。可见,网络已经对样本进行了初步的分类,这种分类不够精准。

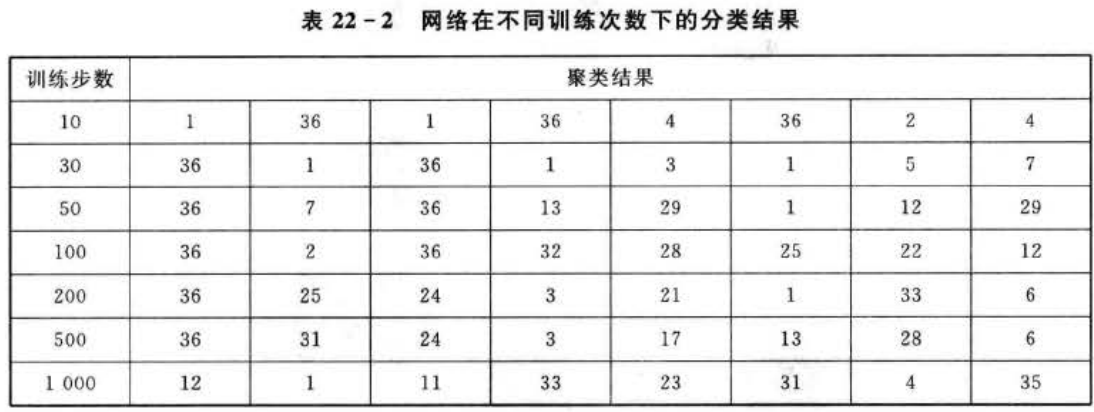
当训练步数为200时,每个样本都被划分为一类。这种分类结果更加细化了。当训练步数为500或者1000时,同样是每个样本都被划分为一类。这时如果再提高训练步数,已经没有实际意义了。网络拓扑学结构如图22-3所示。

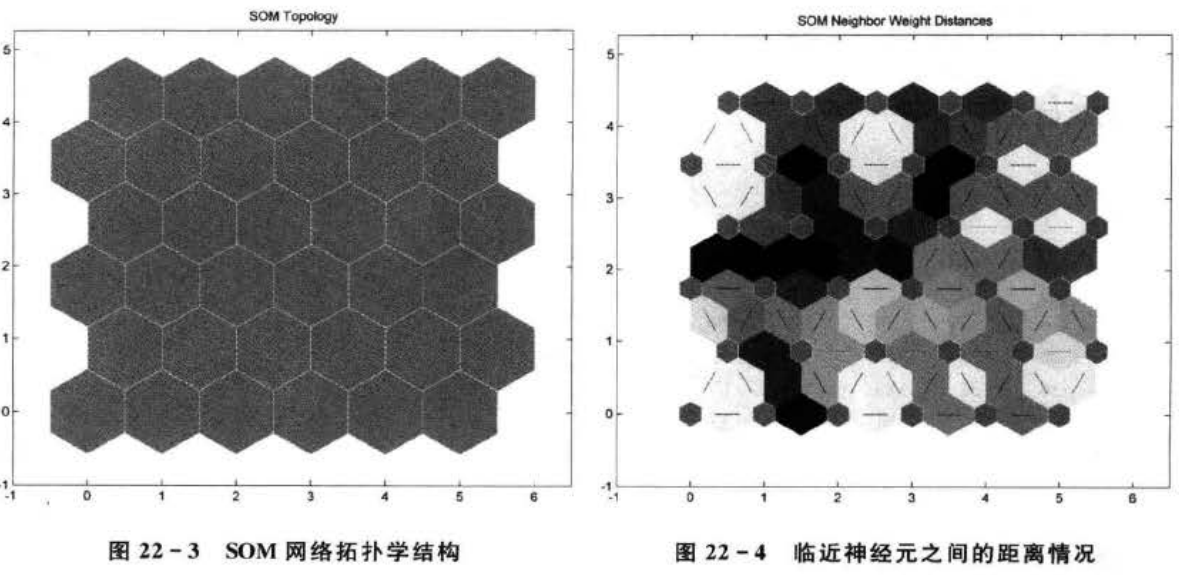
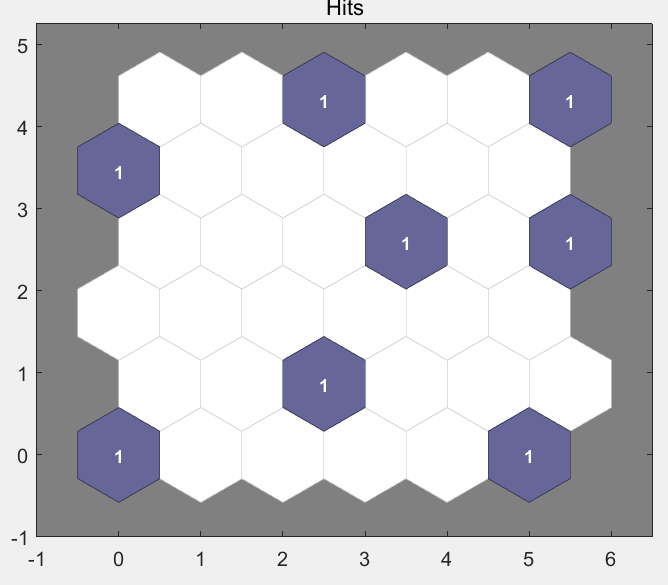
临近神经元直接的距离情况如图22-4所示。每个神经元的分类情况如图22-5所示。
由图22-3可知:竞争层神经元有6×6=36个;在图22-4中,蓝色代表神经元,红色线代表神经元直接的连接,每个菱形中的颜色表示神经元之间距离的远近,从黄色到黑色,颜色越深说明神经元之间的距离越远。图22-5中蓝色神经元表示竞争胜利的神经元

4 案例扩展

4.1SOM网络分类优势

        SOM 网络的训练步数影响网络的聚类性能,本例选择了10100,500次分别进行训练,观察其性能。发现500次就可以将样本完全分开,这样的话,就没有必要训练更多次了。另外，SOM网络在100次就可以很快地将样本进行精确的分类,这比一般方法的聚类速度快。
        SOM程序执行时,每次执行后的结果不一样,原因是每次的激发神经元可能不一样,但是无论激活哪个神经元,最后分类的结果不会改变。

        自组织竞争神经网络算法能够进行有效的自适应分类,但它仍存在一些问题，第一个问题就是学习速度的选择使其不得不在学习速度和最终权值向量的稳定性之间进行折中。第二个问题是有时一个神经元的初始权值向量里输入向量太远以致它从未在竞争中获胜,因而也从未得到学习,这将形成毫无用处的“死”神经元。