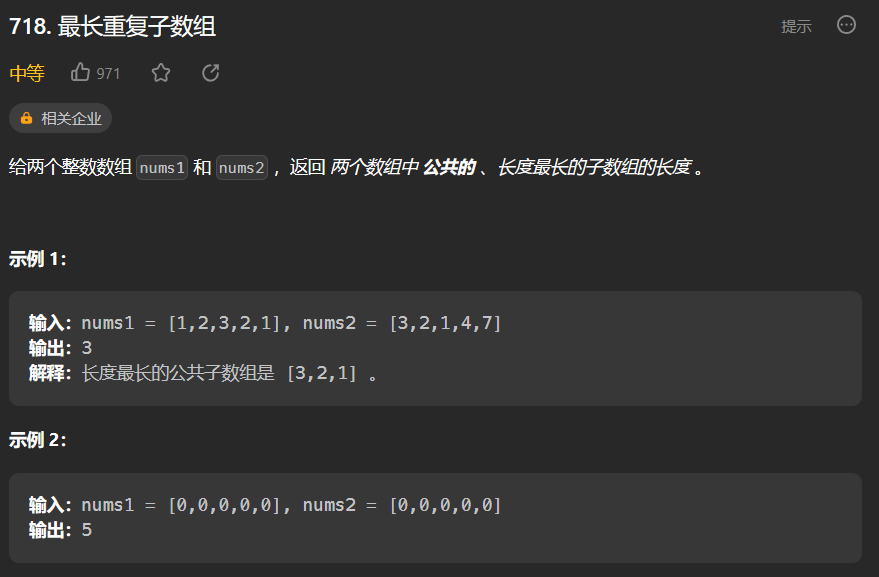
718 最长重复子数组

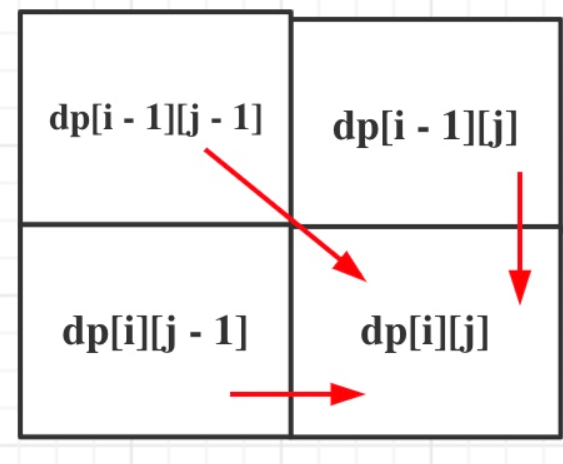
此处求的是连续的子序列，使用动态规划进行求解。
使用dp[i][j]表示第1个序列前i个数字和第2个序列前j个数字的最大的重复子数组长度。

class Solution(object):
    def findLength(self, nums1, nums2):
        """
        :type nums1: List[int]
        :type nums2: List[int]
        :rtype: int
        """
        m, n = len(nums1), len(nums2)
        dp = [[0 for _ in range(n+1)] for _ in range(m+1)]

        max_len = 0
        for i in range(1, m+1):
            for j in range(1, n+1):
                if nums1[i-1] == nums2[j-1]:
                    dp[i][j] = dp[i-1][j-1] + 1

                # if dp[i][j] != 0:
                #     max_len = max(max_len, dp[i][j])

        return max([max(dp_i) for dp_i in dp])

1143 最长公共子序列

子序列和子数组相比, 最大的区别就是是否连续. 当可以不连续的时候我们直接copy在当前情况之前的结果即可.

class Solution(object):
    def longestCommonSubsequence(self, text1, text2):
        """
        :type text1: str
        :type text2: str
        :rtype: int
        """
        m, n = len(text1), len(text2)
        dp = [[0 for _ in range(n+1)] for _ in range(m+1)]

        for i in range(1, m+1):
            for j in range(1, n+1):
                if text1[i-1] == text2[j-1]:
                    dp[i][j] = dp[i-1][j-1] + 1
                else:
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1])

        return max([max(dp_i) for dp_i in dp])

53 最大子数组和

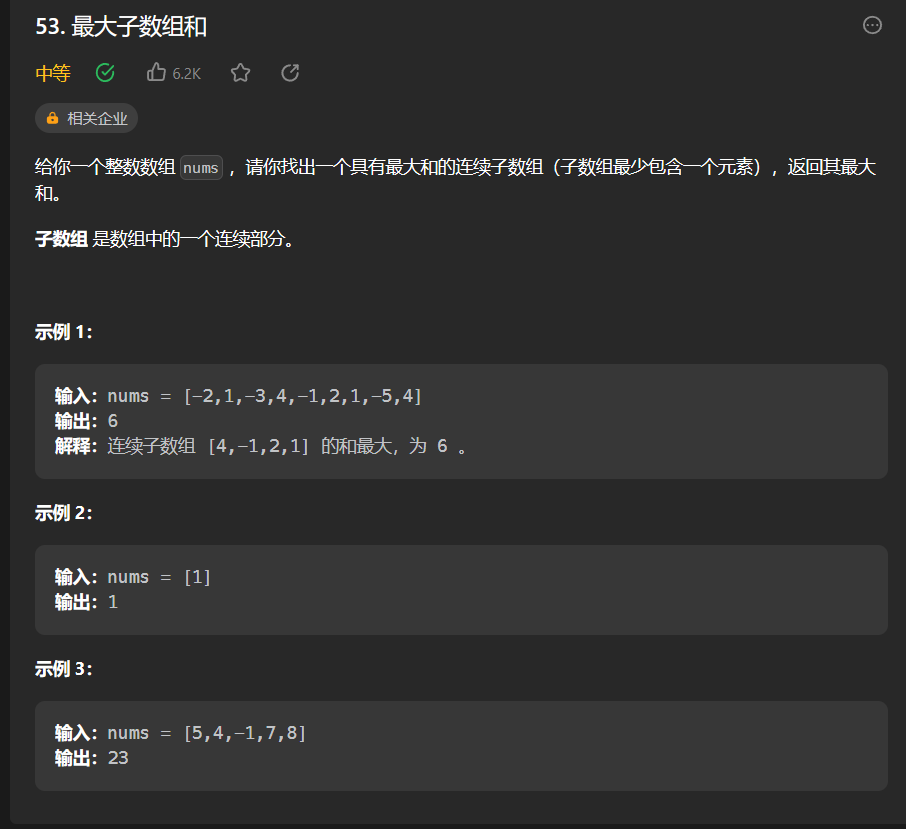
如果前面的和还没有直接从自己开始来的大,就丢弃前面的和.

class Solution(object):
    def maxSubArray(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        n = len(nums)
        dp = [0] * n
        dp[0] = nums[0]

        max_n = dp[0]
        for i, num in enumerate(nums):
            if i == 0:
                continue
            dp[i] = max(dp[i-1] + num, num)
            max_n = max(max_n, dp[i])
        
        return max_n

115 不同的子序列

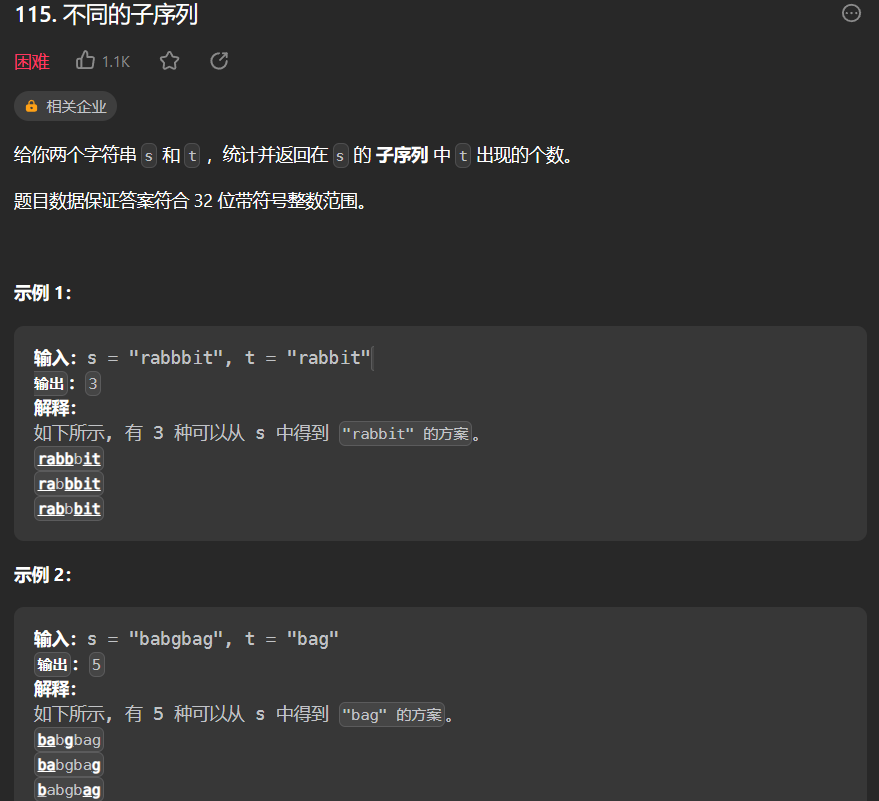
class Solution:
    def numDistinct(self, s: str, t: str) -> int:
        m, n = len(s), len(t)
        if m < n or (m == n and s != t):
            return 0
        
        dp = [[0 for _ in range(n+1)] for _ in range(m+1)]
        for i in range(m+1):
            dp[i][0] = 1
        
        for i in range(1, m+1):
            for j in range(1, n+1):
                if s[i-1] == t[j-1]:
                	# 有不选 和 选两种选择
                    dp[i][j] = dp[i-1][j] + dp[i-1][j-1]
                else:
                    dp[i][j] = dp[i-1][j]
        
        return dp[m][n]

582 两个字符串的删除操作

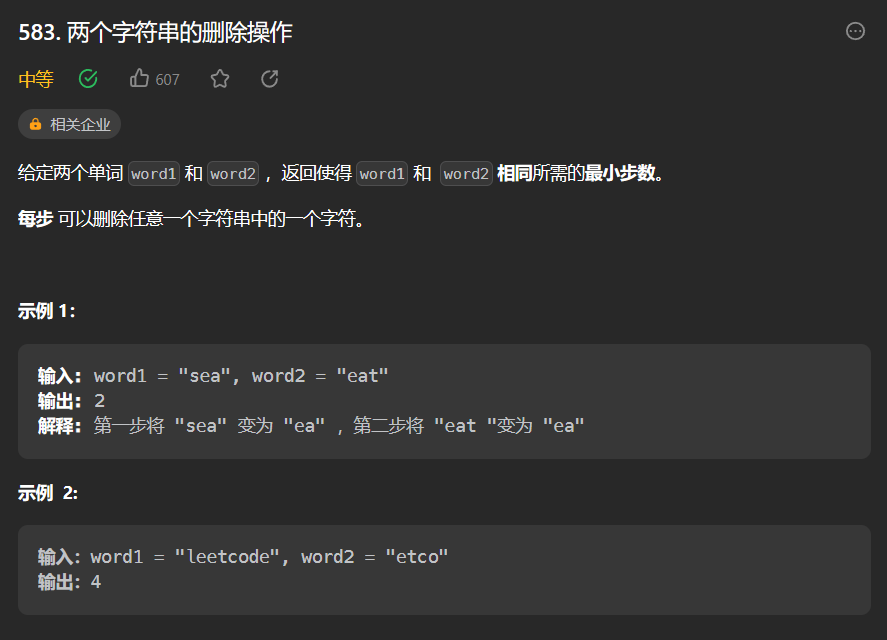
求出最长公共子序列之后算一下长度就好了

class Solution(object):
    def minDistance(self, word1, word2):
        """
        :type word1: str
        :type word2: str
        :rtype: int
        """
        # 以word1[i] word2[j]的最长公共子序列长度
        if len(word1) < len(word2):
            word1, word2 = word2, word1

        m, n = len(word1), len(word2)
        dp = [[0 for _ in range(n+1)] for _ in range(m+1)]

        max_len = 0
        for i in range(1, m+1):
            for j in range(1, n+1):
                if word1[i-1] == word2[j-1]:
                    dp[i][j] = dp[i-1][j-1] + 1
                else:
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1])
                max_len = max(max_len, dp[i][j])
        
        return m + n - 2 * max_len

72 编辑距离

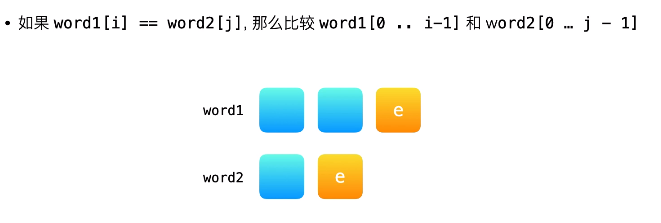
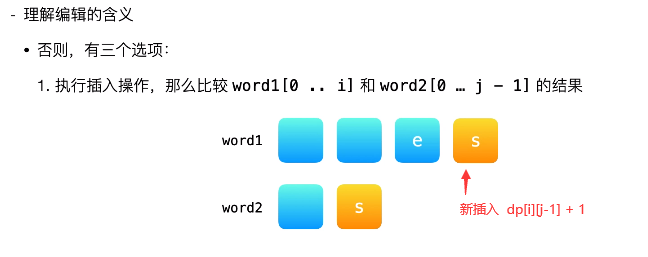
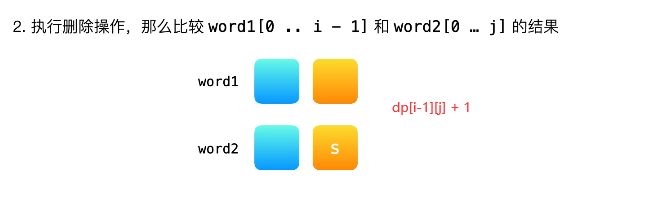
这个根据图来理解各种情况就很好理解.

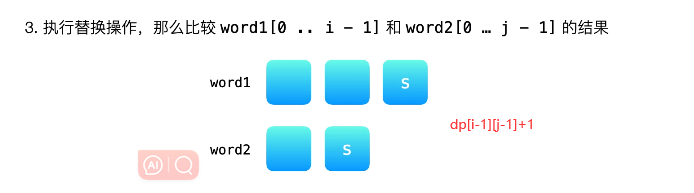
class Solution(object):
    def minDistance(self, word1, word2):
        """
        :type word1: str
        :type word2: str
        :rtype: int
        """
        if len(word1) < len(word2):
            word1, word2 = word2, word1

        m, n = len(word1), len(word2)
        dp = [[0 for _ in range(n+1)] for _ in range(m+1)]

        # 编辑距离是相互的 注意这里的初始化
        for i in range(1, m+1):
            dp[i][0] = i
        for j in range(1, n+1):
            dp[0][j] = j

        for i in range(1, m+1):
            for j in range(1, n+1):
                if word1[i-1] == word2[j-1]:
                    dp[i][j] = dp[i-1][j-1]
                else:
                    # 替换 dp[i-1][j-1] + 1
                    # 删除 dp[i-1][j] + 1
                    # 插入 dp[i][j-1] + 1
                    dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1
        print(dp)
        return dp[-1][-1]