目录
1.字典树
(1)为什么引入字典树
(2)字典树定义
(3)字典树的节点实现
(4)字典树的增删改查
DFA(确定有穷自动机)
(5)优化
1.字典树
(1)为什么引入字典树
匹配算法的瓶颈之一在于如何判断集合(词典)中是否含有字符串。如果用有序集合TreeMap)的话,复杂度是o(logn) ( n是词典大小);如果用散列表( Java的HashMap. Python的dict )的话,账面上的时间复杂度虽然下降了,但内存复杂度却上去了。有没有速度又快、内存又省的数据结构呢?这就是字典树。
(2)字典树定义
字符串集合常用字典树存储,这是一种字符串上的树形数据结构。字典树中每条边都对应一个字,从根节点往下的路径构成一个个字符串。字典树并不直接在节点上存储字符串,而是将词语视作根节点到某节点之间的一条路径,并在终点节点上做个标记"该节点对应词语的结尾".字符串就是一条路径,要查询一个单词,只需顺着这条路径从根节点往下走。如果能走到特殊标记的节点,则说明该字符串在集合中,否则说明不存在。一个典型的字典树如下图所示所示。

其中,蓝色标记着该节点是一个词的结尾,数字是人为的编号。按照路径我们可以得到如下表所示:
| 词语 | 路径 |
|---|---|
| 入门 | 0-1-2 |
| 自然 | 0-3-4 |
| 自然人 | 0-3-4-5 |
| 自然语言 | 0-3-4-6-7 |
| 自语 | 0-3-8 |
当词典大小为 n 时,虽然最坏情况下字典树的复杂度依然是O(logn) (假设子节点用对数复杂度的数据结构存储,所有词语都是单字),但它的实际速度比二分查找快。这是因为随着路径的深入,前缀匹配是递进的过程,算法不必比较字符串的前缀。
(3)字典树的节点实现
我们要用python类来实现字典树,首先要想明白字典树的基本性质,对于每个节点来说,我们需要知道它对应的子节点和对应的边。如果要实现映射的话,还需要知道自己对应的值。·约定用值为None表示节点不对应词语,虽然这样就不能插入值为None的键了,但实现起来更简单。在_add_child方法中,先检查是否已经存在字符char对应的child,然后根据overwrite来决定是否覆盖child的值。通过这样,就可以把子节点连接到父节点上去。
class Node(object):
def __init__(self, value):
self._children = {} # 表示该节点下的分支(孩子,子节点)有哪些,用字典存储:char为键,表示子节点的字。字典的值为分支位置
self._value = value # 理解为节点对应的值,value相当于表示从根节点到这里这是个词,不是词的话就是none,没有含义。
def _add_child(self, char, value, overwrite=False): # overwrite为true就是重写,false就是不重写。
child = self._children.get(char) # 得到该节点在char这条边的子节点
if child = None: # 如果该节点在这个char这没有分支
child = Node(value) # 则新建一个char的分支
self._children[char] = child # 把父节点的char分支位置对应到新建的节点位置,这样就连接起来了。
elif overwrite:
child._value = value # 重写overwrite覆盖掉原来的值
return child # 返回的是child node的位置,即子节点位置视频: 0203字典树Node_哔哩哔哩_bilibili 0203字典树Node_哔哩哔哩_bilibili
比如在字典树中插入“入门”词语

插入“自然人”词语
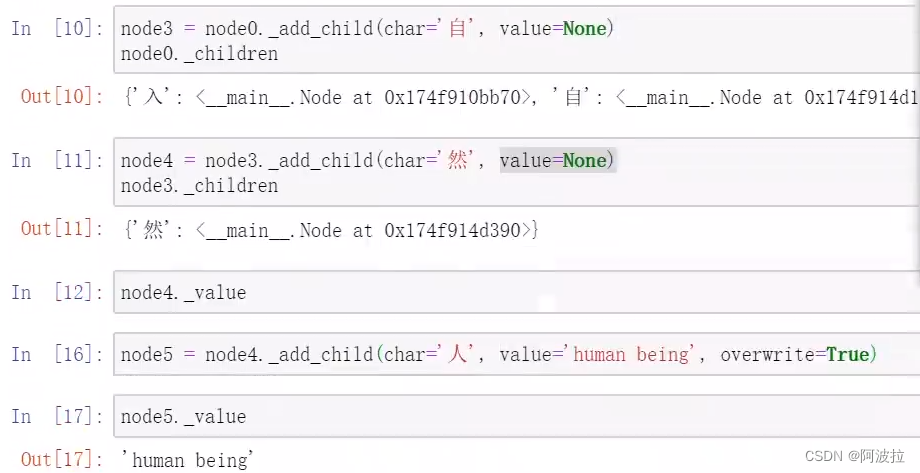
插入“自然”词语

(4)字典树的增删改查
"删改查"其实是一回事,都是查询。删除操作就是将终点的值设为None而已,修改操作无非是将它的值设为另一个值而已。从确定有限状态自动机的角度来讲,每个节点都是一个状态,状态表示当前已查询到的前缀。,从父节点到子节点的转移可以看作一个事件(状态转移)。我们向父节点查询是否有满足状态的边,如果有,则转移状态,当全部转移后,我们会询问该节点(状态)是否为蓝色节点,若是,则查询成功。
DFA(确定有穷自动机)
概念:从一个状态通过一系列事件转换到另一个状态
【过程】:
- 初始状态为空,当触发事件“匹”时转换到状态“匹”;
- 触发事件“配”,转换到状态“匹配”;
- 依次类推,直到转换为最后一个状态“匹配关键词”。
”增加键值对“其实还是查询,只不过在状态转移失败的时候,则创建相应的子节点,保证转移成功。
字典树的完整实现如下:
# 继承于上面的node类
class Trie(Node):
# _init_可理解为“构造函数”,在对象初始化的时候调用,使用传入的参数初始化该实例。
def __init__(self) -> None:
super().__init__(None)
# _contains_用于自定义容器类型,定义调用in和 not in来测试成员是否存在的时候所产生的行为。
def __contains__(self, key):
return self[key] is not None # is not None语法可以认为判断一个变量是否为None
# __getitem_用于自定义容器类型,定义当某一项被访问时,使用 self[key]所产生的行为。
def __getitem__(self, key):
state = self
for char in key:
state = state._children.get(char)
if state is None:
return None
return state._value
# _setitem_用于自定义容器类型,定义执行 self[key]=value 时产生的行为。
def __setitem__(self, key, value):
state = self
# enumerate() 函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列,同时列出数据和数据下标,一般用在 for 循环当中。
for i, char in enumerate(key):
if i < len(key) - 1:
state = state._add_child(char, None, False)
else:
state = state._add_child(char, value, True)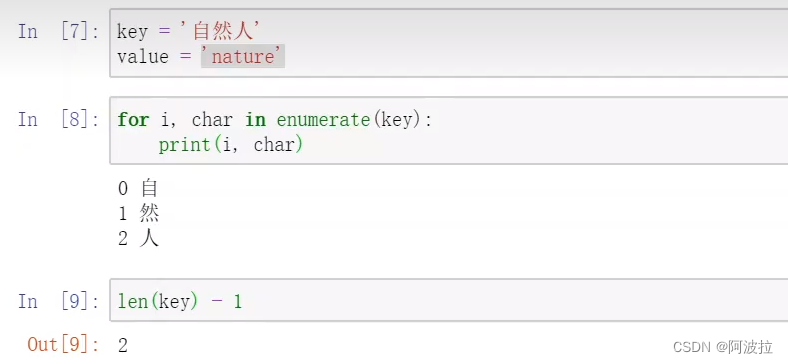
测试:
if __name__ == '__main__':
trie = Trie()
# 增
trie['自然'] = 'nature'
trie['自然人'] = 'human'
trie['自然语言'] = 'language'
trie['自语'] = 'talk to oneself'
trie['入门'] = 'introduction'
assert '自然' in trie # assert是python断言语法,用于判断一个表达式,在表达式条件为 false 的时候触发异常。
# 删
trie['自然'] = None
assert '自然' not in trie
# 改
trie['自然语言'] = 'human language'
assert trie['自然语言'] == 'human language'
# 查
assert trie['入门'] == 'introduction'(5)优化
字典树的数据结构在以上的切分算法中已经很快了,但还有一些基于字典树的算法改进,把分词速度推向了千万字每秒的级别,主要按照以下递进关系优化:
- 首字散列其余二分的字典树
- 双数组字典树
- AC自动机(多模式匹配)
- 基于双数组字典树的AC自动机