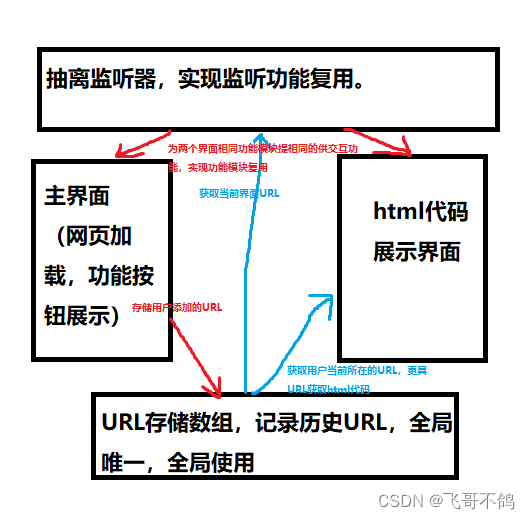
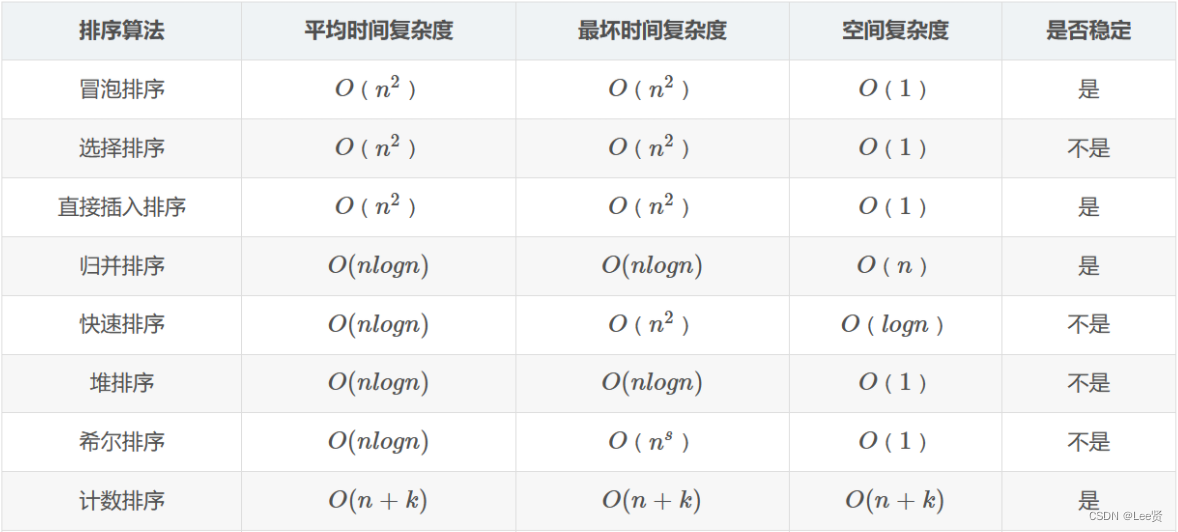
协方差

协方差（Covariance）是统计学中用来衡量两个随机变量之间关系的一种度量。它反映了这两个变量的变化趋势是否一致，即当一个变量偏离其均值时，另一个变量是否也倾向于偏离其均值。协方差可以帮助我们了解变量之间的线性关系以及它们的相互变化情况。

具体而言，对于两个随机变量 X 和 Y，它们的协方差记作 Cov(X, Y)，计算公式如下：

Cov(X, Y) = Σ [(Xᵢ - μₓ) * (Yᵢ - μᵧ)] / (n - 1)

其中：

Xᵢ 和 Yᵢ 分别表示两个变量在第 i 个观测点的取值。
μₓ 和 μᵧ 分别表示 X 和 Y 的均值。
n 表示观测点的数量。

协方差的值有以下几种情况：

若协方差为正值，说明两个变量倾向于一起增加或减少，表现出正相关关系。
若协方差为负值，说明一个变量增加时另一个变量倾向于减少，表现出负相关关系。
若协方差接近于零，说明两个变量之间关系较弱，可能不存在明显的线性关系。

然而，协方差的数值大小受到变量单位的影响，不易直接比较不同数据集之间的关系。因此，人们通常使用标准化后的协方差，即相关系数（Correlation Coefficient），来更好地度量变量之间的关联程度。相关系数范围在 -1 到 1 之间，能够消除单位的影响，更直观地反映变量之间的线性关系程度。

Python

下面是Python代码：

import numpy as np
import matplotlib.pyplot as plt

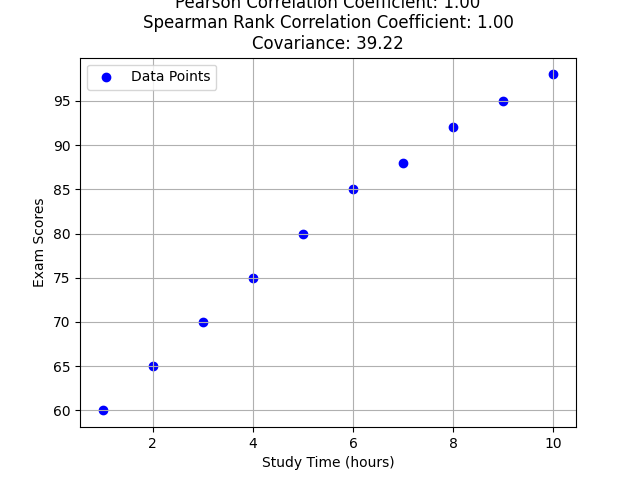
# 示例数据：学习时间（小时）和考试成绩
study_time = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
exam_scores = np.array([60, 65, 70, 75, 80, 85, 88, 92, 95, 98])

# 计算皮尔逊相关系数
correlation_coefficient = np.corrcoef(study_time, exam_scores)[0, 1]
# 计算斯皮尔曼等级相关系数
spearman_corr = np.corrcoef(study_time, exam_scores)[0, 1]

# 计算协方差
covariance = np.cov(study_time, exam_scores)[0, 1]

print(f"Covariance between X and Y: {covariance:.2f}")

# 绘制散点图
plt.scatter(study_time, exam_scores, color='blue', label='Data Points')
plt.title(
    f"Pearson Correlation Coefficient: {correlation_coefficient:.2f}\n"
    f"Spearman Rank Correlation Coefficient: {spearman_corr:.2f}\n"
    f"Covariance: {covariance:.2f}")
plt.xlabel('Study Time (hours)')
plt.ylabel('Exam Scores')
plt.legend()
plt.grid(True)
plt.show()