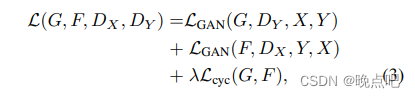题面

john用他的一头母牛和Don先生交换了一头“骑士牛”。这头牛有一个独特的能力——在牧场中能像中国象棋中的马一样跑跳（会中国象棋吗？不会？注意：本题不考虑马被“蹩脚”的情况）。

当然，这头牛不能跳到岩石或树上，不过能跳到有牧草的地方。这儿有一个宽为 X，高为 Y 的矩形牧场(1≤X≤150;1≤Y≤150)。 “骑士牛”和其它牛一样喜欢干草。给你一张包含“骑士牛”出发地和树、岩石、灌木或其它障碍物及大包干草等位置信息的地图，确定“骑士牛”得到干草最少要跳几“跳”。

地图中“骑士牛”出发地用 K表示；障碍物用 * 表示，牧草用 . 表示，干草所在地用 H 表示。这儿有一个示例地图：

骑士牛得到干草的最少步骤在下图中用 ABC…… 表示，最少要跳 5 “跳”（其它的路径可能超过 5 “跳”）：

输入

第 11 行: 两个空格隔开的整数: X 和 Y。

第 2..Y+1 行: 第 Y−i+2 行包含 X 个没有空格的字符（就像上面的地图一样）：表示第i 行的地图。

输出

一个单独的整数表示最少的得到干草的“跳”数。所有的数据都能得到干草。

样例

输入

10 11
..........
....*.....
..........
...*.*....
.......*..
..*..*...H
*.........
...*...*..
.K........
...*.....*
..*....*..

输出

5

跳“牛”版的最短路径，原版戳这 

#include <bits/stdc++.h>
using namespace std;
int fx[9]={0,-1,-2,-2,-1,1,2,2,1},fy[9]={0,-2,-1,1,2,2,1,-1,-2};
char a[160][160];
int n , m , q[40000][4] , tail=1 , head=1;
int s1 , s2 , e1 , e2;
int main(){
	scanf("%d%d" , &m , &n);
	for ( int i = 1 ; i <= n ; i++ ){
		for ( int j = 1 ; j <= m ; j++ ){
			cin >> a[i][j];
			if(a[i][j] == 'K'){
				s1 = i;
				s2 = j;
			}
			if(a[i][j] == 'H'){
				e1 = i;
				e2 = j;
			}
		}
	}	
	q[1][1] = s1;
	q[1][2] = s2;
	q[1][3] = 0;
	int tx , ty;
	while ( head <= tail ){
		for ( int i = 1 ; i <= 8 ; i++ ){
			tx = q[head][1] + fx[i];
			ty = q[head][2] + fy[i];
			if ( a[tx][ty] == '.' || a[tx][ty] == 'H'){
				a[tx][ty] = '*';
				q[++tail][1] = tx;
				q[tail][2] = ty;
				q[tail][3] = q[head][3] + 1;
				if ( tx == e1 && ty == e2 ){
					printf("%d" , q[tail][3]);
					return 0;
				}
			}
		}
		head++;
	}
	return 0;
}