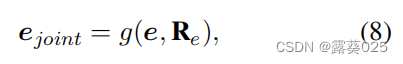一，前言

# 计算优势函数
for t in reversed(range(gen_len)):
    nextvalues = values[:,t + 1] if t < gen_len - 1 else last_values  # 获取下一个时间步的值，如果当前时间步是最后一个时间步，则使用 last_values
    delta = rewards[:, t] + self.config.gamma * nextvalues - values[:,t]  # 计算 delta，即当前时间步的奖励加上折扣因子乘以下一个时间步的值减去当前时间步的值
    lastgaelam = delta + self.config.gamma * self.config.lam * lastgaelam  # 计算 GAE-Lambda，即 delta 加上折扣因子乘以 Lambda 倍的上一个时间步的 GAE-Lambda
    advantages_reversed.append(lastgaelam)  # 将计算得到的 GAE-Lambda 添加到 advantages_reversed 列表中
advantages = torch.stack(advantages_reversed[::-1]).transpose(0, 1)  # 将 advantages_reversed 列表转换为张量，并进行维度转置

二，值函数的损失（Value Function Loss）的计算

值函数的损失公式通常使用均方差（Mean Squared Error，MSE）来衡量值函数的预测误差。值函数的损失公式可以表示为：

L(θ) = 0.5 * E[(V(s) - R)^2]

其中，L(θ)表示值函数的损失，θ表示值函数的参数，V(s)表示值函数对状态s的预测值，R表示实际的回报值。

这个公式的含义是，首先，通过 clip_by_value 函数将当前状态的价值函数 values 限制在一个区间内，得到 vpredclipped。然后，分别计算使用原始价值函数和限制后的价值函数计算得到的损失，即 vf_losses1 和 vf_losses2。通过计算值函数对状态的预测值与实际回报值之间的差异的平方，来衡量值函数的预测误差。然后取这些差异的平方的期望值，再乘以0.5，得到最终的损失值。最终，将两者的较大值作为值函数的损失，通过 masked_mean 函数计算期望。

            # 值函数的损失
            vpredclipped = clip_by_value(
                values, values - self.config.cliprange_value, values + self.config.cliprange_value
            )
            vf_losses1 = (values - returns) ** 2
            vf_losses2 = (vpredclipped - returns) ** 2
            vf_loss = 0.5 * masked_mean(torch.max(vf_losses1, vf_losses2), masks)
            vf_clipfrac = masked_mean(torch.gt(vf_losses2, vf_losses1).double(), masks)

三，策略函数的损失（Policy Function Loss）的计算：

这部分对应公式

在PPO算法中，我们采用两种不同的方式计算策略损失，即pg_losses和pg_losses2。这两种方式分别对应目标函数中的两个部分。

pg_losses表示使用原始比率计算得到的损失，即：

其中，N表示采样轨迹的数量， 表示第 i 条轨迹在时间步 t 的重要性采样比例，表示第 i 条轨迹在时间步 t 的优势函数。

pg_losses2表示使用限制后的比率计算得到的损失，即：

其中， 表示第i条轨迹在时间步t的比率，表示剪切幅度。

最终，将两种方式计算得到的损失取较大值，即：

pg_loss = \max(pg_losses, pg_losses2)

            # 策略函数的损失
            logprobs = F.log_softmax(logits, dim=1)
            ratio = torch.exp(logprobs - old_logprobs)
            pg_losses = -advantages * ratio
            pg_losses2 = -advantages * torch.clamp(ratio, 1.0 - self.config.cliprange, 1.0 + self.config.cliprange)
            pg_loss = masked_mean(torch.max(pg_losses, pg_losses2), masks)
            pg_clipfrac = masked_mean(torch.gt(pg_losses2, pg_losses).double(), masks)

总损失计算

            # 总损失
            loss = pg_loss + self.config.vf_coef * vf_loss

四， 完整代码可以参考：

GitHub - Pillars-Creation/ChatGLM-RLHF-LoRA-RM-PPO: ChatGLM-6B添加了RLHF的实现，以及部分核心代码的逐行讲解 ,实例部分是做了个新闻短标题的生成