模拟退火算法(Simulated Annealing, SA)的思想借 鉴于固体的退火原理,当固体的温度很高的时候,内能比
较大,固体的内部粒子处于快速无序运动,当温度慢慢降 低的过程中,固体的内能减小,粒子的慢慢趋于有序,最
终,当固体处于常温时,内能达到最小,此时,粒子最为 稳定。模拟退火算法便是基于这样的原理设计而成。
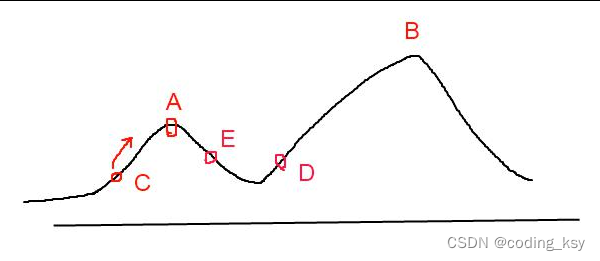 模拟退火算法过程
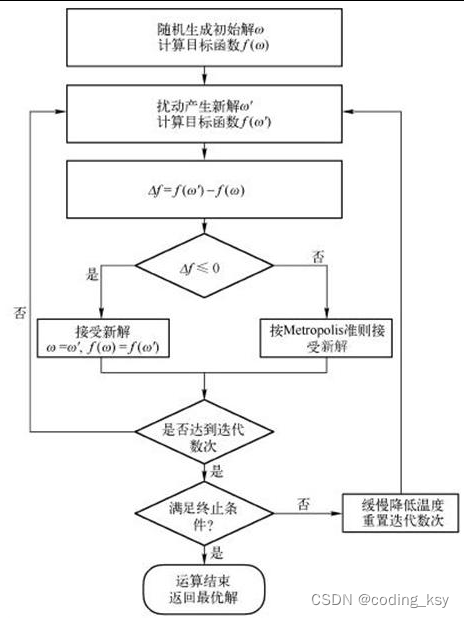
模拟退火算法过程
(1)随机挑选一个单元k,并给它一个随机的位移,求出系统因此而产生的能
量变化ΔEk。
(2)若ΔEk⩽ 0,该位移可采纳,而变化后的系统状态可作为下次变化的起点;
若ΔEk>0,位移后的状态可采纳的概率为
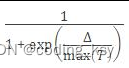
式中T为温度,然后从(0,1)区间均匀分布的随机数中挑选一个数R,若R<Pk,
则将变化后的状态作为下次的起点;否则,将变化前的状态作为下次的起点。
(3)转第(1)步继续执行,知道达到平衡状态为止。
利用模拟退火算法工具箱求解问题:
%%
clc;clear;
%%普通的目标函数
fun = @dejong5fcn %目标函数
%[x,fval] = simulannealbnd(fun,[0,0])%[0,0]凭经验猜测的初始值,没有的话,随意写就行
options = saoptimset('PlotFcns',{@saplotbestx,@saplotbestf,@saplotx,@saplotf})
x0 = [0,0];
lb = [-64,-64];%下限
ub = [64,64];%下限
[x,fval] = simulannealbnd(fun,x0,lb,ub,options);
%%
求:
% min f(x) = (4 - 2.1*x1^2 + x1^4/3)*x1^2 + x1*x2 + (-4 + 4*x2^2)*x2^2;
% 写成函数形式
% function y = simple_objective(x)
% y = (4 - 2.1*x(1)^2 + x(1)^4/3)*x(1)^2 + x(1)*x(2) + (-4 + 4*x(2)^2)*x(2)^2;
%%
fun = @simple_objective;%注意需要将其放在最前面
X0 = [0.5 0.5]; % 初始点
lb = [-64 -64];
ub = [64 64];
[x,fval,exitFlag,output] = simulannealbnd(fun,X0,lb,ub);
fprintf('The number of iterations was : %d\n', output.iterations);
fprintf('The number of function evaluations was : %d\n', output.funccount);
fprintf('The best function value found was : %g\n', fval);
%%
% 求:
% min f(x) = (a - b*x1^2 + x1^4/3)*x1^2 + x1*x2 + (-c + c*x2^2)*x2^2;
%
% 写成函数形式
% function y = parameterized_objective(x,a,b,c)
% y = (a - b*x(1)^2 + x(1)^4/3)*x(1)^2 + x(1)*x(2) + (-c + c*x(2)^2)*x(2)^2;
%%带有常数的目标函数
a = 4; b = 2.1; c = 4; % define constant values
fun = @(x) parameterized_objective(x,a,b,c);
X0 = [0.5 0.5];
options = saoptimset('PlotFcns',{@saplotbestx,@saplotbestf,@saplotx,@saplotf})
[x,fval] = simulannealbnd(fun,X0,options)
%自定义目标函数1
function y = parameterized_objective(x,a,b,c)
y = (a - b*x(1)^2 + x(1)^4/3)*x(1)^2 + x(1)*x(2) + (-c + c*x(2)^2)*x(2)^2;
end
%自定义目标函数2
function y = simple_objective(x)
y = (4 - 2.1*x(1)^2 + x(1)^4/3)*x(1)^2 + x(1)*x(2) + (-4 + 4*x(2)^2)*x(2)^2;
end
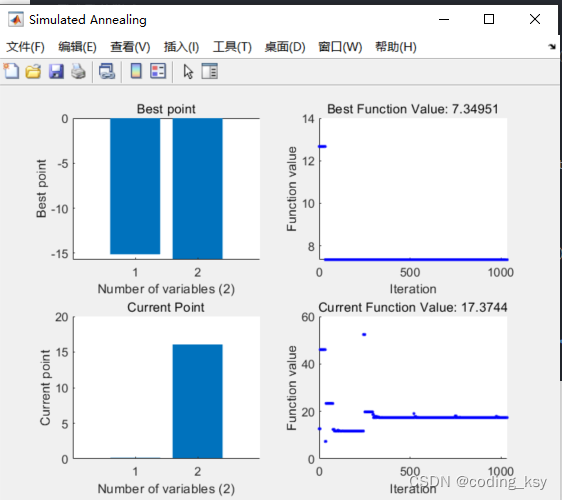
运行效果