前面两篇是讲经典网络ResNet的：

ResNet1

ResNet2

这个残差网络结构非常的经典，所以有不少后续的研究都是基于这个网络的改进，这一篇就来说一说其中的一个经典改进：随机动态网络——Stochastic Depth。
论文：Deep Networks with Stochastic Depth
论文提供了基于lua的代码：https://github.com/yueatsprograms/Stochastic_Depth

基本结构

论文的基本出发点还是想解决如下几个深度网络中的关键问题：

• 梯度消失问题
• 训练时间过长的问题
• Diminishing feature reuse，特征重用。其实我理解和梯度消失很类似，就是在前向和反向传播的过程中，信息流(information flow)或者是梯度(反向)在多层网络中传播的时候，经过多个卷积层相乘之后逐渐消失的现象。

解决这个问题的基本逻辑也很简单，就是随机的让ResNet中的一些层失效，也就是在ResNet中，让残差网络的部分失效，直接通过Skip Connection传播(训练过程)。所以，失效的部分以Residual block为单位，也就是一个block失效或者生效。
论文原文：
We start with very deep networks but during training, for each mini-batch, randomly drop a subset of layers and bypass them with the identity function。

还有一段是：

We resolve this conflict by creating deep Residual Network architectures (with hundreds or even thousands of layers) with sufficient modeling
capacity; however, during training we shorten the network significantly by randomly removing a substantial fraction of layers independently for each sample or mini-batch。

和Dropout层的逻辑很像，只是Dropout的逻辑是让反向传播中的一些权重的梯度随机的变成0。而Stochastic Depth方法是让整个残差结构失效，与dropout不同的点还在于：

• Stochastic Depth可以调整整个网络的深度和宽度。
• dropout没法和BN层一起使用，或者说合并在一起使用没什么用。
• Stochastic Depth可以模拟多个层次的网络，相当于可以综合不同深度的ResNet结果。
  原文中的描述为：One explanation for our performance improvements is that training with stochastic depth can be viewed as training an ensemble of ResNets implicitly. Each of the L layers is either active or inactive, resulting in $2^L$ possible network combinations. For each training mini-batch one of the $2^L$ networks (with shared weights) is sampled and updated.

ResNet的公式改造

论文是基于ResNet的结构来进行改造的。

• 基本Residual block结构为：Conv-BN-ReLU-Conv-BN。
• CIFAR的数据集是使用这个结构，ImageNet使用的是称作Bottlenect的residual block。

论文中的重点就是如何确定哪些block失效，哪些不失效。其实逻辑非常简单：

• 论文中是训练过程中引入了一个Bernoulli random随机概率函数，计作 b l ∈ { 0 , 1 } b_l \in \lbrace 0, 1\rbrace bl​∈{0,1}。

• 每个block的残差部分乘以这个概率，也就是根据这个概率来确定是否生效，论文中称作“survival probability”，计作$p_l=Pr(b_l=1)$。

• 基于上述的逻辑，那么ResNet中的那个经典公式就可以改造为：
  $$H_l=ReLU(b_l{f}_l(H_{l-1})+id(H_{l-1}))$$

• 这个$p_l$在论文中提出了两种分布函数：

  • $p_l$为固定值，每个block的概率是一样的。
  • $p_l$为一个线性分布，服从函数：
    $$p_l=1-\frac{l}{L}(1-p_L)$$
    论文中给出了一个图：

大概的意思就是越到后面的层就越容易失效。

根据上面的逻辑，$p_L$就称为了一个超参数，并且论文中通过实验证明，$p_L=0.5$时效果最好。

效果计算

关于论文要解决的其中一个问题，就是减少训练时间或者说计算量，论文也给出了一个估算方式：
在训练过程中的有效block数可以通过一个随机变量$\hat{L}$来表示(因为其中增加了随机变量$p_l$)，这个随机变量的期望就可以表示为：
$$E(\hat{L})=\sum _{l=1}^L{p}_l$$

根据上面的$p_l$的线性分布，另外加上$p_L=0.5$的话，这个期望计算出来就是：
$$E(\hat{L})=(3L-1)/4\approx 3L/4$$
后面的约等于是在L较大，也就是网络层数较深的情况下成立。

所以，在ResNet-110的网络结构下，总共有L=54(L为block数)，那么在训练过程中有效的block数就是$54\ast 3/4\approx 40$。也就是相对于原网络，减少了14个block(约1/4)，在训练时的运算量或者说时间。

前向传播过程

因为在反向传播时，一些卷积层中的权重有时是失效的，学到的参数不那么完全，所以在前向传播，也就是推理过程中，也要增加这个随机变量$p_l$：
$$H_l^{Test}=ReLU(p_l{f}_l(H_{l-1}^{Test},W_l)+H_{l-1}^{Test})$$

原文对此的描述是：From the model ensemble perspective, the update rule (5) can be interpreted
as combining all possible networks into a single test architecture, in which each
layer is weighted by its survival probability

实验结果

• 论文中是使用的ResNet为基本网络。
• 对于网络中的第一个Res block，也就是$p_0=1$，保证第一个block总是有效。
• 使用的基本都是线性的概率分布，令$p_L=0.5$
• 在数据集CIFAR-10，CIFAR-100使用的是110层的ResNet(ResNet的第一篇论文中提到过，不过我没有写到我的前一篇文章中，有兴趣的朋友可以去看一下原文，总共3组Block，共18个res blocks，filter number分别为16，32，64)。

总共是在CIFAR-10，CIFAR-100，SVHN，ImageNet四个数据集上对一些网络做了对比，结果如下：

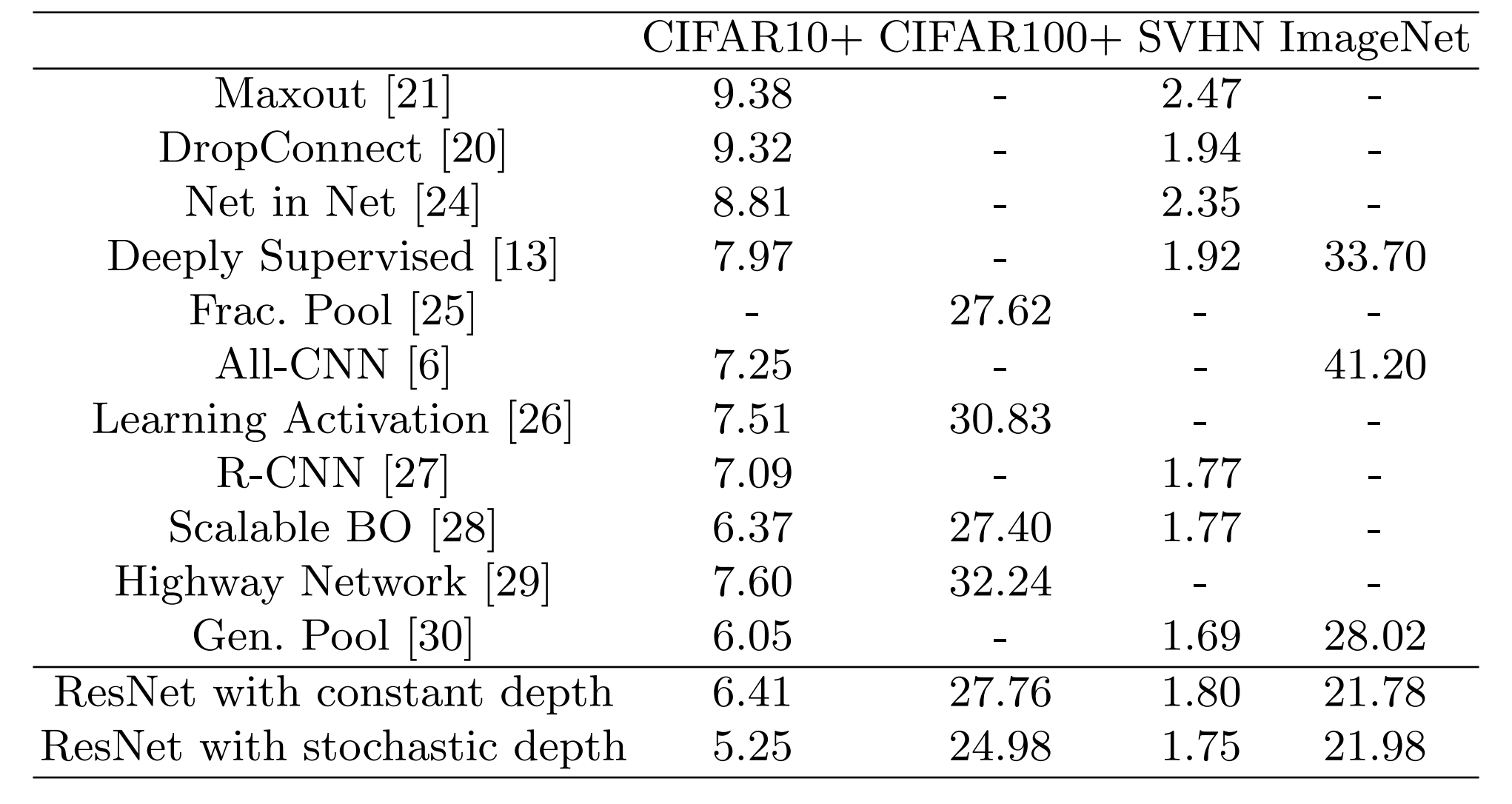
CIFAR数据集结果

在test error和trainning loss上，把普通的resnet和增加了Stochastic depth的网络做了比较

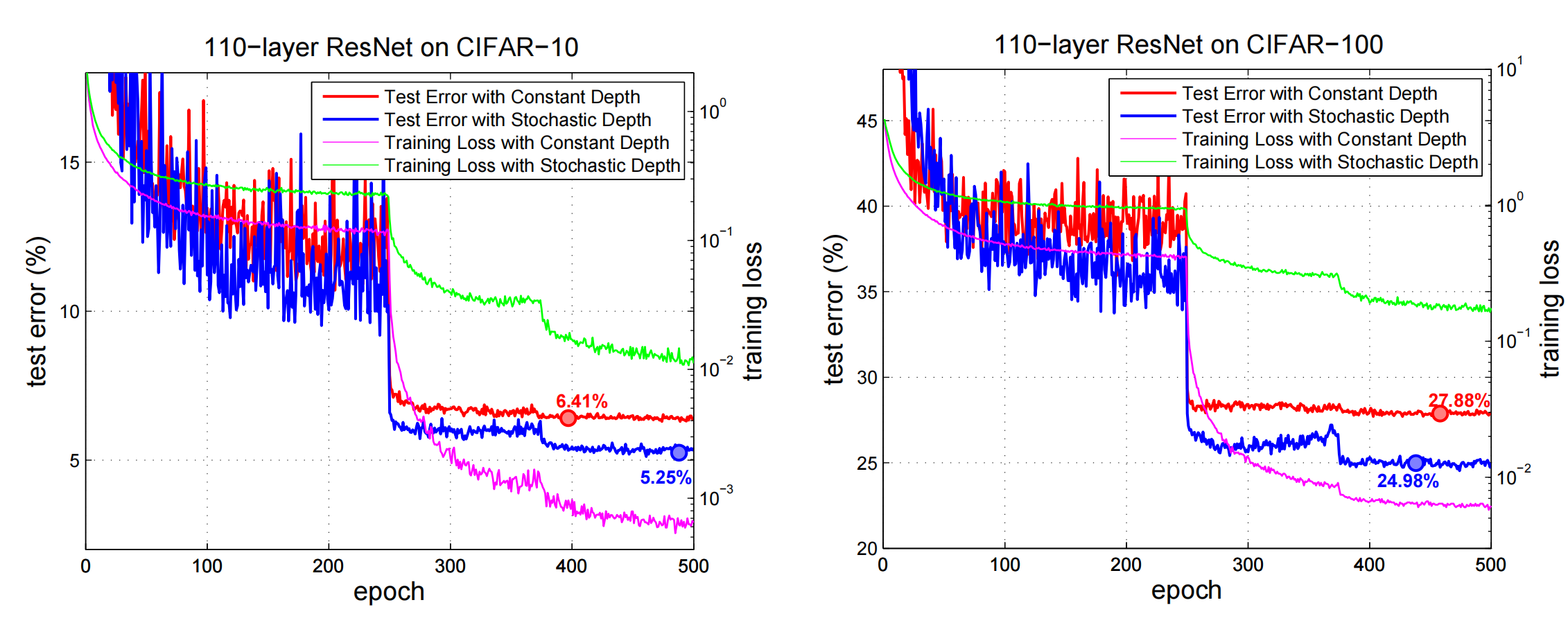
• test error有更好的效果
• trainning loss没有下降的那么快，也就是说对保持梯度有正向的效果，对避免梯度消失问题也有正向的效果。
• 在两个数据集上有类似的效果

SVHN数据集结果

SVHN数据集是Street View House Number，来自于Google街景。
对于SVHN使用的是ResNet-152的网络结构。

• 和CIFAR类似的结论，只是没那么明显
• 与普通的ResNet网络相比，Stochastic depth还不会出现过拟合的现象。普通的ResNet网络在第30个epoch往后就出现了过拟合的现象。

训练时间的比对

这个不用多说，训练时间减少了1/4，和前面计算的差不多。

极深网络的对比测试

在ResNet中，作者提出了一个1202的网络，但是表现不佳，出现了过拟合的现象，还没有101层的网络表现好。在这篇论文中，作者把Stochastic depth结构增加到了这个极深网络中，解决了这个过拟合的问题。

• 300个epoch的训练
• 前10个epoch的学习率为0.01，后面恢复成0.1

• 普通的resnet，深度从101到1202的话，test error从6.41%增加到了6.67%。
• Stochastic depth网络，深度从101到1202的话，test error从5.25%下降到了4.91%。
• 也就是说，在极深的网络中使用Stochastic depth是会有帮助的，可以使用非常深的网络来拟合数据了。
• 网络越深，节省的计算时间也就越多。

ImageNet的测试结果

使用的是ResNet-152的网络深度，而且使用的是bottleneck的残差结构。
论文中的实验在ImageNet上没有前面几个数据集一样好的结果。

测试过程中的结果

• 在大概epoch=90的时候，Stochastic depth网络的错误率还是要高出一点点。
• 但是论文指出说，我既然节省了约1/4的时间，那么我多训练30个epoch，到达120个epoch，错误率就可以下降到21.98%。
• 然后再多训练30个epoch，也就是训练150个epoch，错误率就可以下降到21.78%。
• 从上面的结论来看，作者的意思是对于ImageNet这种大数据集，必须继续增加深度来获得更好的结果：Although there seems to be no immediate benefit from applying stochastic depth on this particular architecture, it is possible that stochastic depth will lead to improvements on ImageNet with larger models。

网络结构的Hyper-parameter比对测试

论文中还对网络结构中的Hyper-parameter，也就是$p_L$进行了一些比对测试。这个测试是基于ResNet-110的。
比对了使用固定$p_L$和线性$p_L$的结果：

• $p_L$设置的合适的话，比基本的ResNet结果要好。
• linear decay rule比uniform要好。
• 最佳区域在0.4-0.8之间
• 0.5是最好的，所以上面的测试网络都是用的0.5这个值。

论文中还提供了一个热点图：

这个图提供的是网络深度和超参数$p_L$之间的关系。证明足够深的网络使用stochastic是有效的，即使深度不够，也会有一定的帮助。
原文为：A deep enough model is necessary for stochastic depth to significantly outperform the baseline (an observation we also make with the ImageNet data
set), although shorter networks can still benefit from less aggressive skipping。