一、灰色系统
- 白色系统:系统信息完全明确
- 灰色系统:系统部分信息已知,部分信息未知
- 对在一定范围内变化的、与时间有关的灰色过程进行预测。
- 过程:原始数据找规律→生成强规律性的数据序列→建立微分方程来预测未来趋势
- 黑色系统:系统的内部信息未知
二、GM(1,1)模型: Grey(Gray) Model
2.1 基本概念及原理
-
GM(1,1)是使用原始的离散非负数据列,通过一次累加生成削弱随机性的较有规律的新的离散数据列 → 通过建立微分方程模型,得到在离散点处的解经过累减生成的原始数据的近似估计值 → 从而预测原始数据的后续发展。
- 本节只探究GM(1,1)模型,第一个‘1’表示微分方程是一阶的,后面的‘1’表示只有一个变量
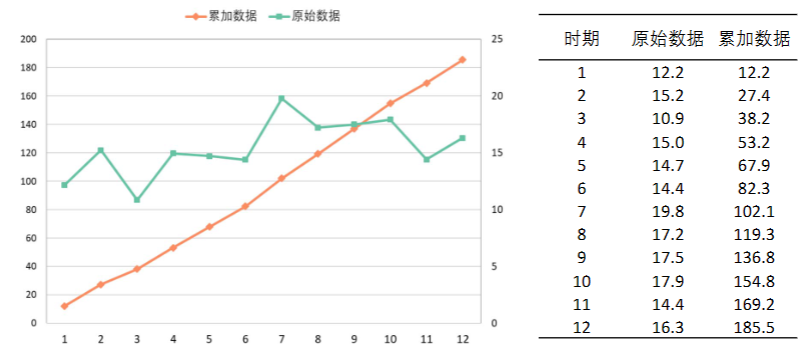
- 本节只探究GM(1,1)模型,第一个‘1’表示微分方程是一阶的,后面的‘1’表示只有一个变量
-
原理介绍:(见第12节课件P4-15)
-
GM(1,1)模型的本质是有条件的指数拟合:f(x) = C1eC2(x-1) (此处的指数规律主要针对x(1)(k)序列而言,原始序列是作差的结果)
-
GM(1,1)模型的白化方程:
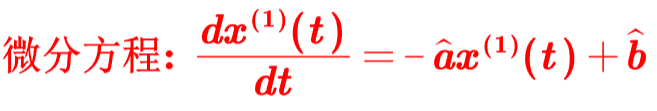
-
GM(1,1)模型的基本形式(亦称灰色微分方程):
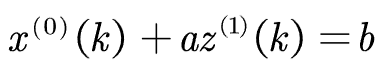
2.2 准指数规律的检验
实际建模中,要计算出ρ(k)∈(0,0.5)的占比,占比越高越好(一般前两期:ρ(2)和ρ(3)可能不符合要求,重点关注后面的期数)
2.3 发展系数与预测情形
- 发展系数越小,预测得越精确
2.4 GM(1,1)模型的评价
- 使用GM(1,1)模型对未来的数据进行预测时,需要先检验GM(1,1)模型对原数据的拟合程度(对原始数据还原的效果)。一般有两种检验方法:
2.4.1 残差检验

- 注:
- ① 其他预测模型也可以用这个残差检验
- ② 关于这个10%和20%的标准不是绝对的,要结合预测的场景(如物理中对精确要求高的,也可是5%)
2.4.2 级别偏差检验

2.5 GM(1,1)模型的拓展:新陈代谢模型

2.6 适用灰色预测的情况
- 数据是以年份度量的非负数据(如果是月份或者季度数据一定要用时间序列模型);
- 数据能经过准指数规律的检验(除了前两期外,后面至少90%的期数的光滑比要低于0.5);
- 数据的期数较短且和其他数据之间的关联性不强(≤10,也不能太短了,比如只有3期数据),要是数据期数较长,一般用传统的时间序列模型比较合适。
三、示例:对长江水质污染的预测
3.1 题目
- 2005年国赛A题中给出长江在过去10年中废水排放总量,如果不采取保护措施,请对今后10年的长江水质污染的发展趋势做出预测。

3.2 预测题目的一些tips
- 看到数据后先画时间序列图并简单的分析下趋势(例如:之前的时间序列分解);
- 将数据分为训练组和试验组,尝试使用不同的模型对训练组进行建模,并利用试验组的数据判断哪种模型的预测效果最好(例如:可用SSE指标来挑选模型,常见的模型有指数平滑、ARIMA、灰色预测、神经网络等)。
- 选择上一步骤中得到的预测误差最小的那个模型,并利用全部数据来重新建模,并对未来的数据进行预测。
- 画出预测后的数据和原来数据的时序图,看看预测的未来趋势是否合理。
3.3 GM(1,1)模型代码讲解


- 画出原始数据的时间序列图,并判断原始数据中是否有负数或期数是否低于4期,如果是的话则报错,否则执行下一步;
- 对一次累加后的数据进行准指数规律检验,返回两个指标:
- 指标1:光滑比小于0.5的数据占比(一般要大于60%)
- 指标2:除去前两个时期外,光滑比小于0.5的数据占比(一般大于90%)并让用户决定数据是否满足准指数规律,满足则输入1,不满足则输入0
- 如果上一步用户输入0,则程序停止;如果输入1,则继续下面的步骤。
- 让用户输入需要预测的后续期数,并判断原始数据的期数:
- 数据期数为4:分别计算出传统的GM(1,1)模型、新信息GM(1,1)模型和新陈代谢GM(1,1)模型对于未来期数的预测结果,为了保证结果的稳健性,对三个结果求平均值作为预测值。
- 数据期数为5,6或7:取最后两期为试验组,前面的n‐2期为训练组;用训练组的数据分别训练三种GM模型,并将训练出来的模型分别用于预测试验组的两期数据;利用试验组两期的真实数据和预测出来的两期数据,可分别计算出三个模型的SSE;选择SSE最小的模型作为我们建模的模型。
- 数据期数大于7:取最后三期为试验组,其他的过程和4.2类似。
- 输出并绘制图形显示预测结果,并进行残差检验和级比偏差检验。
四、神经网络预测示例
4.1 题目:辛烷值的预测
- 【改编】辛烷值是汽油最重要的品质指标,传统的实验室检测方法存在样品用量大,测试周期长和费用高等问题,不适用于生产控制,特别是在线测试。近年发展起来的近红外光谱分析方法(NIR),作为一种快速分析方法,已广泛应用于农业、制药、生物化工、石油产品等领域。其优越性是无损检测、低成本、无污染,能在线分析,更适合于生产和控制的需要。
- 实验采集得到50组汽油样品(辛烷值已通过其他方法测量),并利用傅里叶近红外变换光谱仪对其进行扫描,扫描范围900~1700nm,扫描间隔为2nm,即每个样品的光谱曲线共含401个波长点,每个波长点对应一个吸光度。
- (1)请利用这50组样品的数据,建立这401个吸光度和辛烷值之间的模型。
- (2)现给你10组新的样本,这10组样本均已经过近红外变换光谱仪扫描,请预测这10组新样本的辛烷值。
4.2 数据的导入
- 注意:在matlab下,当导入文件出错时,要注意如下两点
- 导入数据
- Excel操作小技巧:选择某个单元格的数据,同时按住键盘上的Ctrl+Shift两个键不松手,然后按键盘上方向键“→”,就可以选择这个单元格所在的一行;然后再按键盘上的方向键“↓”,就可以再选取这一行所在的一整列。
- Excel操作小技巧:选择某个单元格的数据,同时按住键盘上的Ctrl+Shift两个键不松手,然后按键盘上方向键“→”,就可以选择这个单元格所在的一行;然后再按键盘上的方向键“↓”,就可以再选取这一行所在的一整列。
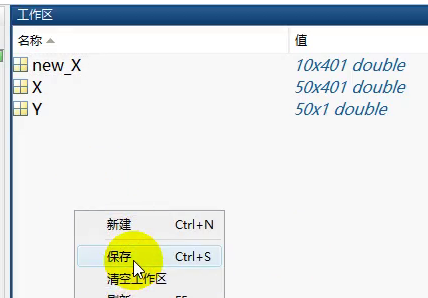
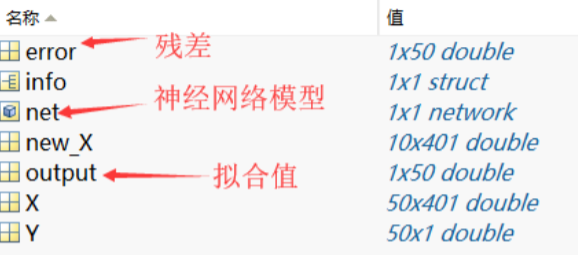
- 保存数据(data_Octane.mat)
- X:50个样本的吸光度数据
- Y:50个样本的辛烷值数据
- new_X:10个要预测样本的吸光度数据
4.3 神经网络模型
- 不同版本的神经网络模型位置可能不同,可自行上网查看
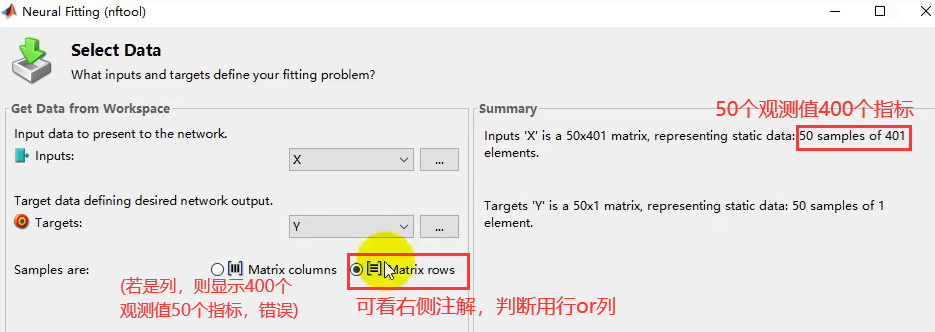
- 根据样本放在行上还是列上来选择。
- 训练集、验证集、测试集的比例一般选择默认的即可。(Matlab会后台自动帮我们安装这个比例来随机抽取样本,因此每次运行的结果可能都不相同)
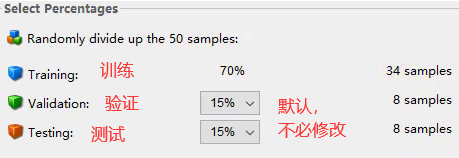
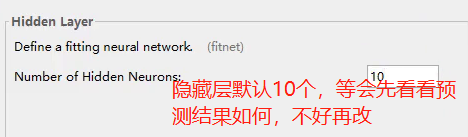
- 隐层神经元的个数,这个参数可以根据拟合的结果再次进行调整。
- 训练算法的选取,一般是选择默认即可,选择完成后点击按钮后,Matlab就会帮我们训练出一个神经网络模型。
- ①莱文贝格-马夸特方法(Levenberg–Marquardt algorithm)能提供数非线性最小化(局部最小)的数值解。此算法能借由执行时修改参数达到结合高斯‐牛顿算法以及梯度下降法的优点,并对两者之不足作改善(比如高斯‐牛顿算法之反矩阵不存在或是初始值离局部极小值太远)
- 经过少数几次即可收敛
- ②贝叶斯正则化方法(Bayesian‐regularization)
- 可以处理过拟合,但训练很慢
- 推荐采用该方法,拟合效果一般是最好的,MSE一般是三个中最小的(越小拟合越好);但由于速度过慢,对机器要求高,故方法①和③用的也多
- ③量化共轭梯度法(Scaled Conjugate Gradient ):《模式识别与智能计算–MATLAB技术实现》
- 每次迭代速度很快,但需要很多次的收敛
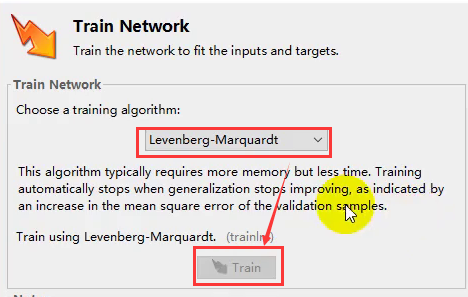
- 每次迭代速度很快,但需要很多次的收敛
- ①莱文贝格-马夸特方法(Levenberg–Marquardt algorithm)能提供数非线性最小化(局部最小)的数值解。此算法能借由执行时修改参数达到结合高斯‐牛顿算法以及梯度下降法的优点,并对两者之不足作改善(比如高斯‐牛顿算法之反矩阵不存在或是初始值离局部极小值太远)
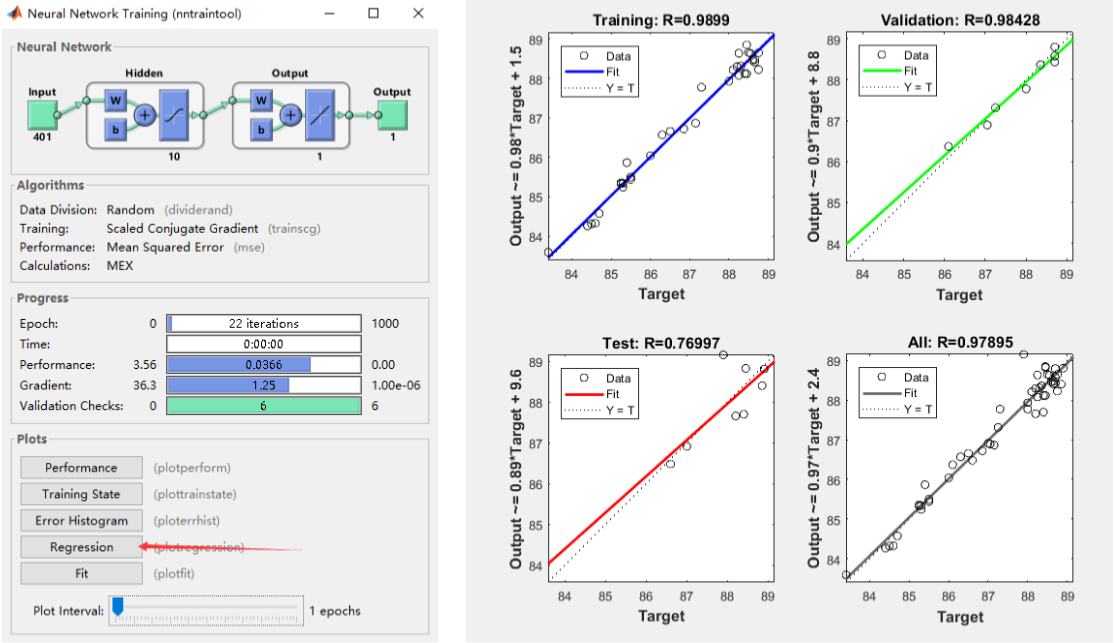
4.4 结果分析
- epoch:1个epoch等于使用训练集中的全部样本训练一次,每训练一次,神经网络中的参数经过调整。
- MSE: Mean Squared Error 均方误差
- MSE = SSE/n。一般来说,经过更多的训练阶段后,误差会减小,但随着网络开始过度拟合训练数据,验证数据集的误差可能会开始增加。在默认设置中,在验证数据集的MSE连续增加六次后,训练停止,最佳模型对应于的最小MSE。
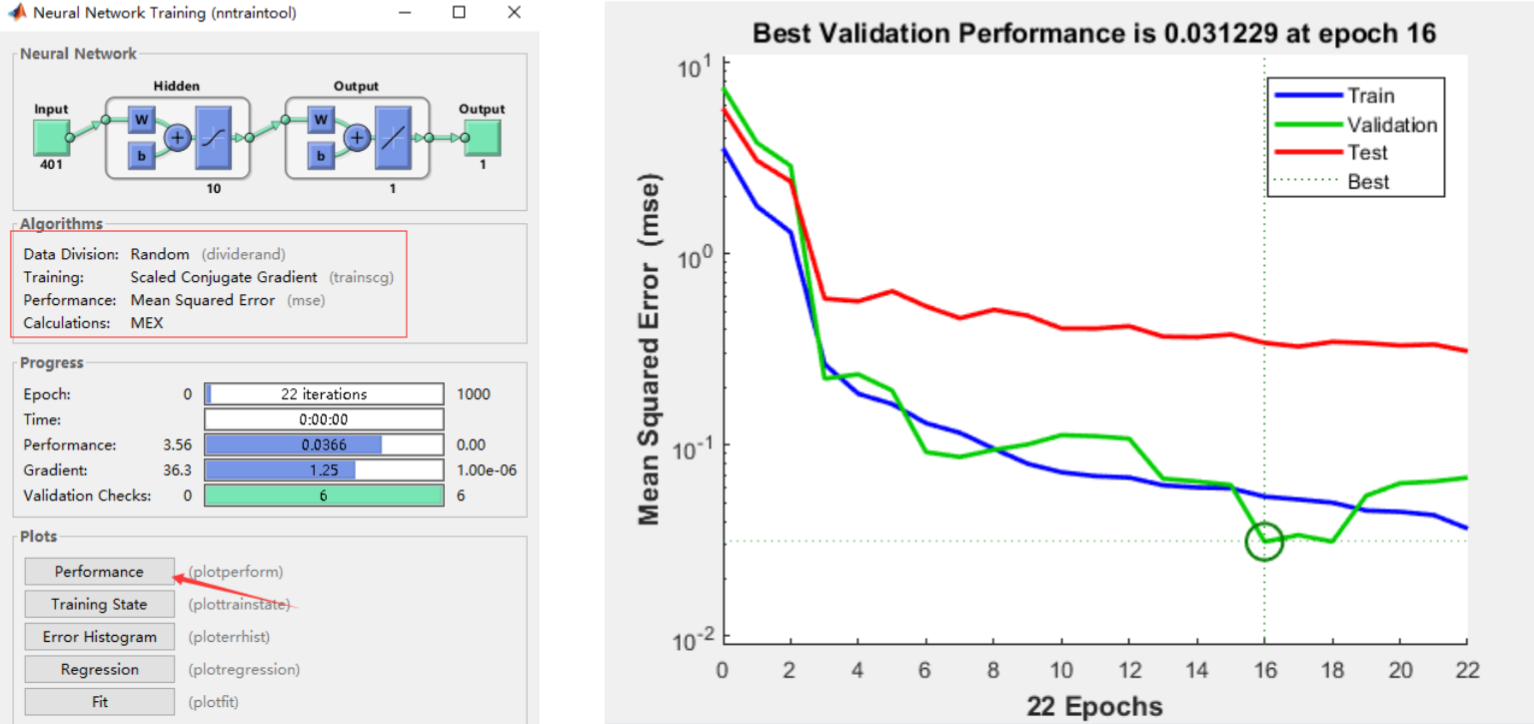
- MSE = SSE/n。一般来说,经过更多的训练阶段后,误差会减小,但随着网络开始过度拟合训练数据,验证数据集的误差可能会开始增加。在默认设置中,在验证数据集的MSE连续增加六次后,训练停止,最佳模型对应于的最小MSE。
- 将拟合值对真实值回归,拟合优度越高,说明拟合的的效果越好。
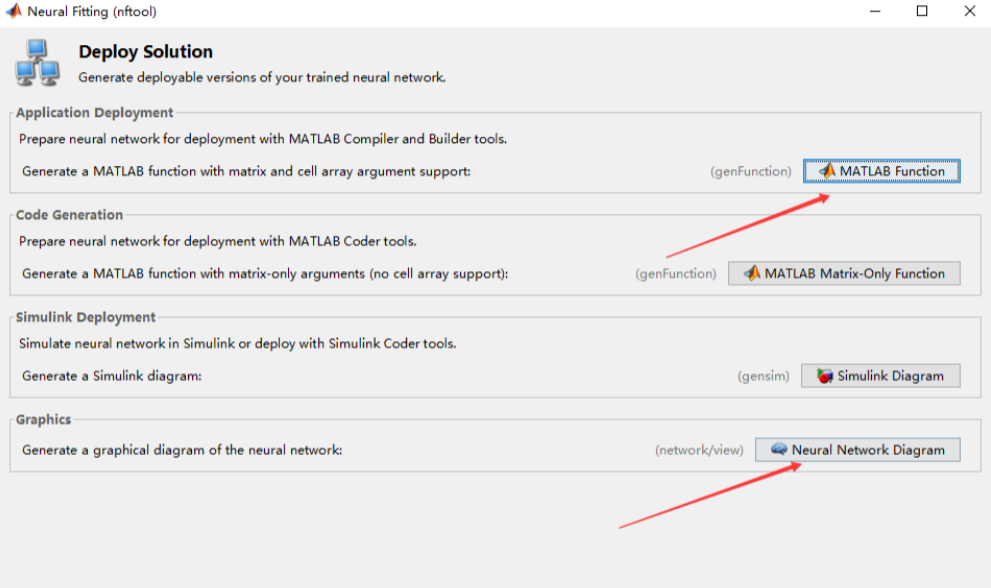
4.5 保存结果
- 保存神经网络函数的代码,以及神经网络图。
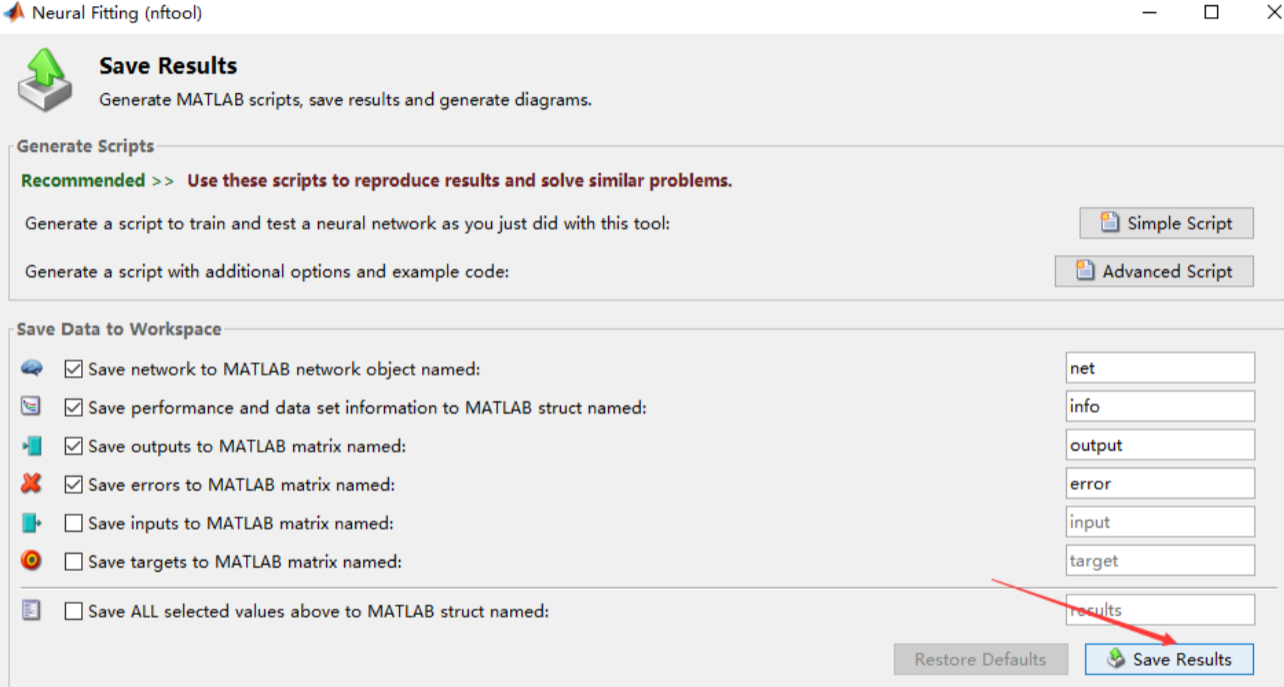
- 保存好训练出来的神经网络模型和结果
4.6 进行预测
- 保存code_Octane.m
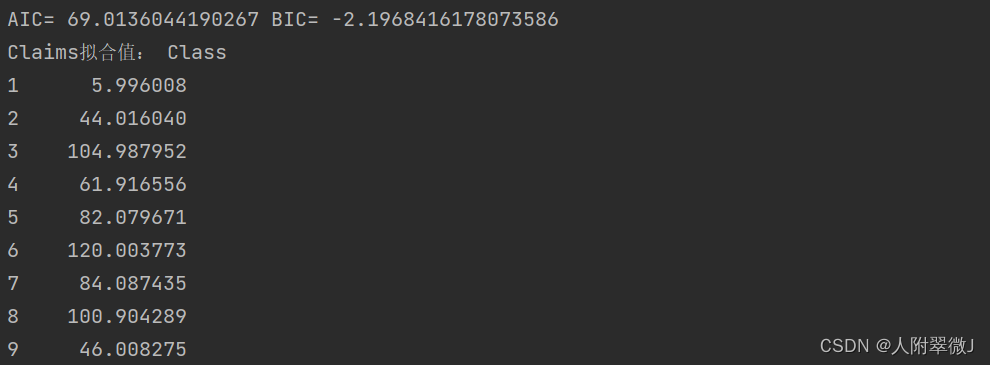
- 残差 + 拟合值 = 真实值
% 这里要注意,我们要将指标变为列向量,然后再用sim函数预测
sim(net, new_X(1,:)')
% 写一个循环,预测接下来的十个样本的辛烷值
predict_y = zeros(10,1); % 初始化predict_y
for i = 1: 10
result = sim(net, new_X(i,:)');
predict_y(i) = result;
end
disp('预测值为:')
disp(predict_y)
4.7 神经网络处理过拟合思路
- 将已知数据留尾部一小部分,用作训练出结果后的测试,计算MSE等看看大小 (有分析过程,体现有处理过拟合现象的意识)
- 或切换不同模型训练
4.8 其他:神经网络在多输出中的运用
- 多输出:多个Y值
- 过程如上,神经网络也能在多输出中使用