本篇文章来详细介绍一下二叉树链式结构经常使用的相关函数,以及相关的的OJ题。
目录
1.前置说明
2.二叉树的遍历
2.1 前序、中序以及后序遍历
2.2 层次遍历
3.节点个数相关函数实现
3.1 二叉树节点个数
3.2 二叉树叶子节点个数
3.3 二叉树第k层节点个数
3.4 在二叉树中查找值为x的节点
4.二叉树基础oj练习
5.二叉树的创建和销毁
5.1 通过前序遍历构建二叉树
5.2 销毁二叉树
5.3 判断二叉树是否为完全二叉树
1.前置说明
在学习链式二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入,为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
//创造树节点
BTNode* BuyNode(BTDataType x)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
if (newnode == NULL)
{
perror("malloc fail");
return NULL;
}
newnode->data = x;
newnode->left = newnode->right = NULL;
return newnode;
}
// 构建二叉树
BTNode* CreatBinaryTree()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->Left = node2;
node1->Right = node4;
node2->Left = node3;
node4->Right = node5;
node4->Left = node6;
return node1;
}注意:上述代码并不是创建二叉树的方式,真正创建二叉树方式后面详解重点讲解。
再看二叉树基本操作前,再回顾下二叉树的概念,二叉树是:
- 空树
- 非空:根节点,根节点的左子树、根节点的右子树组成的。
创建的二叉树图解:
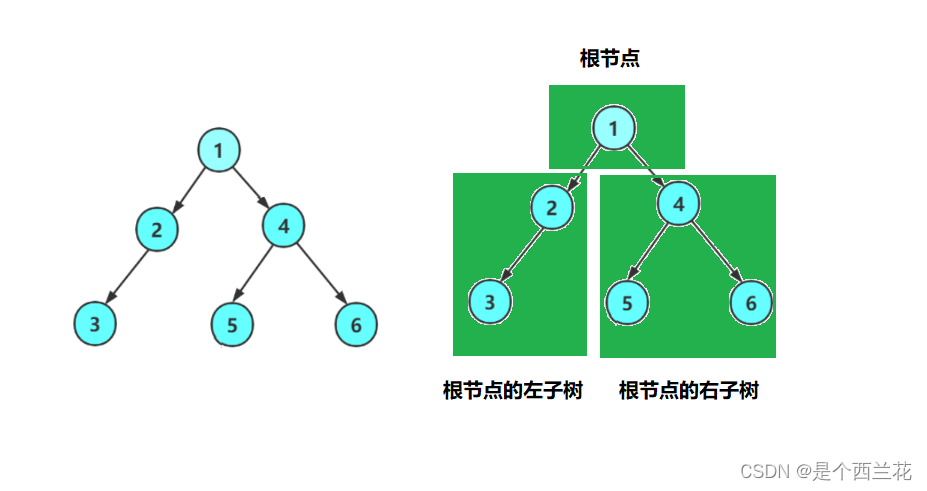
从概念中可以看出,二叉树定义是递归式的,因此后序基本操作中基本都是按照该概念实现的。
2.二叉树的遍历
2.1 前序、中序以及后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
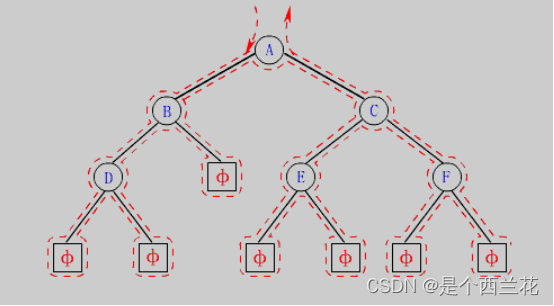
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
- 前序遍历(Preorder Traversal亦称先序遍历)――访问根结点的操作发生在遍历其左右子树之前。
- 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
- 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);三个函数实现起来非常相似,只是访问数据的顺序不同。
具体实现:
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{
if (root==NULL)
{
printf("# ");
return;
}
printf("%c ",root->data);
BinaryTreePrevOrder(root->left);
BinaryTreePrevOrder(root->right);
}
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
if (root == NULL)
{
printf("#");
return;
}
BinaryTreePrevOrder(root->left);
printf("%c ", root->data);
BinaryTreePrevOrder(root->right);
}
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
if (root == NULL)
{
printf("#");
return;
}
BinaryTreePrevOrder(root->left);
BinaryTreePrevOrder(root->right);
printf("%c ", root->data);
}下面主要分析前序递归遍历,中序与后序图解类似,大家可自己动手绘制。
前序遍历递归图解:
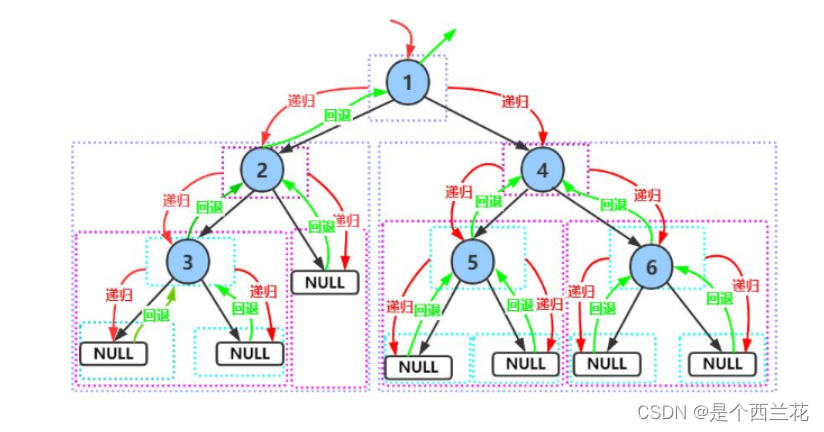
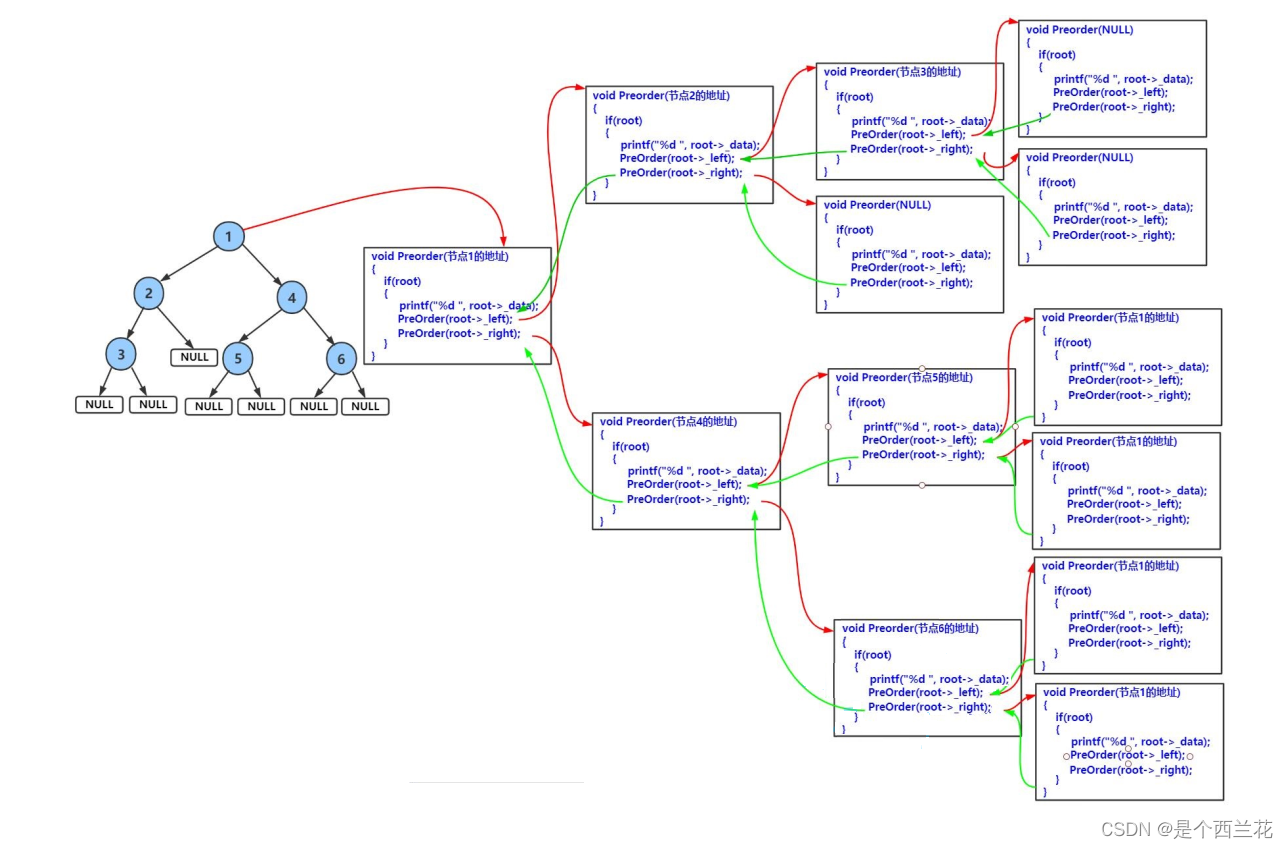
前序遍历结果:1 2 3 4 5 6
中序遍历结果:3 2 1 5 4 6
后序遍历结果:3 2 5 6 4 1
2.2 层次遍历
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
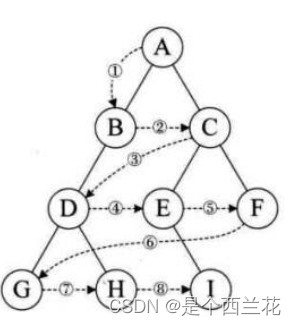
那么我们怎么实现呢?
这里需要使用队列,让根节点先入堆,再出队,出队时让左右子树入堆,空树不进队,按照这个方式可以实现二叉树的层次遍历。
具体实现:这里队列相关函数要自己实现,C++就方便多了,以后会讲。
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
//创建一个队列
Queue q;
//初始化队列
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%c ", front->data);
if (front->left)
{
QueuePush(&q, front->left);
}
if (front->right)
{
QueuePush(&q, front->right);
}
}
printf("\n");
QueueDestroy(&q);
}3.节点个数相关函数实现
3.1 二叉树节点个数
=左子树的节点数+右子树的节点数+根节点数。根节点数为1。
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}3.2 二叉树叶子节点个数
=左子树的叶子节点数+右子树的叶子节点数。
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->right == NULL && root->left == NULL)
{
return 1;
}
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}3.3 二叉树第k层节点个数
=左子树的K-1层节点数+右子树的K-1层节点数。
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
assert(k > 0);
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
3.4 在二叉树中查找值为x的节点
=根节点不是,就在左子树和右子树中寻找
//在二叉树中查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
return root;
}
BTNode* left = BinaryTreeFind(root->left, x);
BTNode* right = BinaryTreeFind(root->right, x);
return left == NULL ? right : left;
}4.二叉树基础oj练习
- 单值二叉树。OJ链接
- 检查两颗树是否相同。OJ链接
- 对称二叉树。OJ链接
- 二叉树的前序遍历。OJ链接
- 二叉树中序遍历。OJ链接
- 二叉树的后序遍历。OJ链接
- 另一颗树的子树。OJ链接
5.二叉树的创建和销毁
二叉树的构建及遍历。OJ链接
5.1 通过前序遍历构建二叉树
通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树,'#'代表空。
代码实现:
//开辟树节点空间
BTNode* BuyNode(char x)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
newnode->data = x;
newnode->left = newnode->right = NULL;
return newnode;
}
//构建树
BTNode* CreatTree(char* arr,int*i)
{
if(arr[*i] =='#')
{
(*i)++;
return NULL;
}
BTNode* node = BuyNode(arr[*i]);
(*i)++;
node->left = CreatTree(arr,i);
node->right = CreatTree(arr,i);
return node;
}
int main()
{
char arr[] = "ABD##E#H##CF##G##";
int i = 0;
//传递下标的地址,这样就可以通过地址修改下标。
BTNode* tree = CreatTree(arr, &i);
return 0;
}5.2 销毁二叉树
这里是后序思想,先释放左右子树,最后释放根节点。
// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{
if (*root == NULL)
{
return;
}
BinaryTreeDestory(&((*root)->left));
BinaryTreeDestory(&((*root)->right));
free(*root);
*root = NULL;
}5.3 判断二叉树是否为完全二叉树
这里也是通过队列进行判断,之前层次遍历空树不进队,而这里空树进队,当出队时遇到空时,停止出队,判断队列中是否有非空,如果有就不是完全二叉树。
代码实现:
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
if (front != NULL)
{
QueuePop(&q);
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
else
{
//遇到空就跳出
break;
}
}
//检查后面节点有没有非空
//有非空就不是完全二叉树
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front != NULL)
return 0;//不是
}
return 1;//是
}本篇结束!


![[Linux]计算机软硬体系结构](https://img-blog.csdnimg.cn/img_convert/8fc74792cde195d99b15075896aa0a13.png)