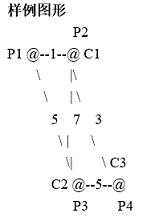
5.6哈夫曼树及其应用
5.6.1哈夫曼树的基本概念
路径:从树中一个结点到另一个结点之间的分支构成这两个结点间的路径。
结点的路径长度:两结点间路径上的分支数。
树的路径长度:从树根到每一个结点的路径长度之和。记作 TL
结点数目相同的二叉树中,完全二叉树是路径长度最短的二叉树
权(weight):将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。
结点的带权路径长度:从根结点到该结点之间的路径长度与该结点的权的乘积。
树的带权路径长度:树中所有叶子结点的带权路径长度之和。
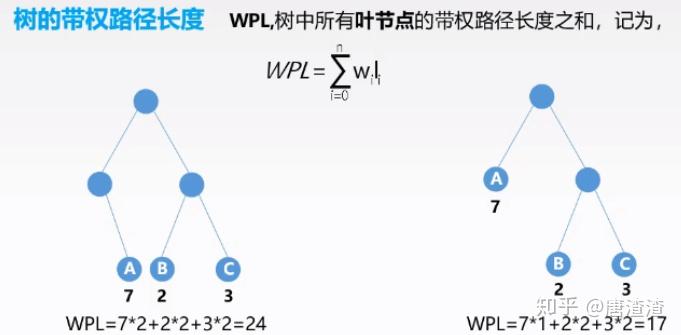
哈夫曼树:最优树 带权路径长度(WPL)最短的树
注意:“带权路径长度最短”是在“度相同”的树中比较而得的结果,因此有最优二叉树、最优三叉树之称等等。
哈夫曼树:最优二叉树 带权路径长度(WPL)最短的二叉树
因为构造这种树的算法是由哈夫曼教授于1952年提出的,所以被称为哈夫曼树,相应的算法称为哈夫曼算法。
哈夫曼树的特点:
满二叉树不一定是哈夫曼树
哈夫曼树中权越大的叶子离根越近
具有相同带权结点的哈夫曼树不唯一
5.6.2哈夫曼树的构造算法
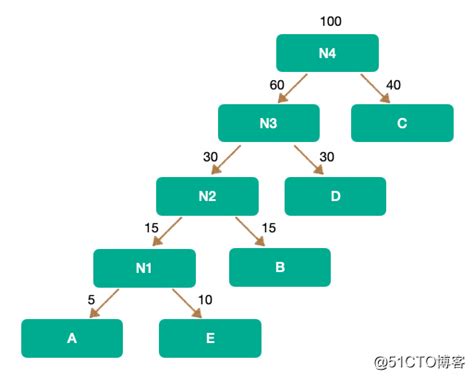
哈夫曼树中权越大的叶子离根越近
贪心算法:构造哈夫曼树时首先选择权值小的。
哈夫曼算法(构造哈夫曼树的方法)
- 根据 n 个给定的权值{W1,W2,…,Wn}构成 n 棵二叉树的森林F={T1,T2,…,Tn},其中Ti只有一个带权为Wi的根结点。
- 构造森林全是根
- 在F中选取两棵根结点的权值最小的树作为左右子树,构造一棵新的二叉树,且设置新的二叉树的根结点的权值为其左右子树上根结点的权值之和。
- 选用两小造新树
- 在F中删除这两棵树,同时将新得到的二叉树加入森林中。
- 删除两小添新人
- 重复(2)和(3),直到森林中只有一棵树为止,这棵树即为哈夫曼树。
- 重复2、3剩单根
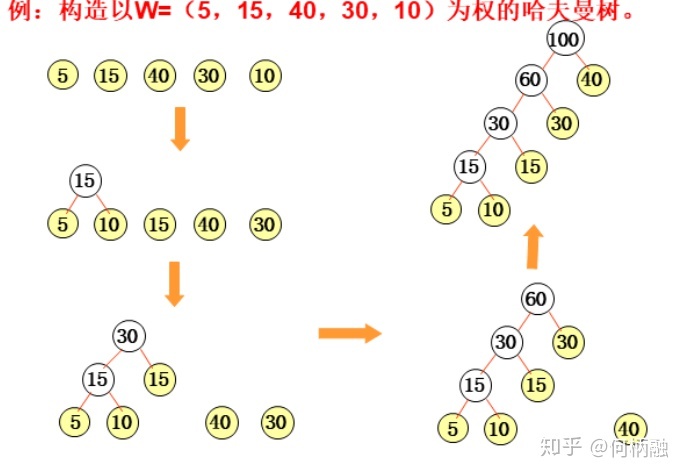
哈夫曼树的结点的度数为0或2,没有度为1的结点。
包含 n 个叶子结点的哈夫曼树中共有 2n-1 个结点。
包含 n 棵树的森林要经过 n-1 次合并才能形成哈夫曼树,共产生 n-1 个新结点。

总结:
- 在哈夫曼算法中,初始时有 n 棵二叉树,要经过 n-1 次合并最终形成哈夫曼树。
- 经过 n-1 次合并产生 n-1 个新结点,且这 n-1 个新结点都是具有两个孩子的分支结点。
- 哈夫曼树中共有 n+n-1=2n-1 个结点,且其所有的分支结点的度均不为1。
5.6.3哈夫曼树构造算法的实现
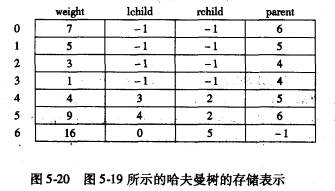
采用顺序存储结构——一维结构数组
结点类型定义:
typedef struct{
int weight;
int parent,lch,rch;
}HTNode,*HuffmanTree;
-
初始化HT[1…2n-1]:lch = rch = parent = 0;
-
输入初始 n 个叶子结点:置HT[1…n]的weight值;
-
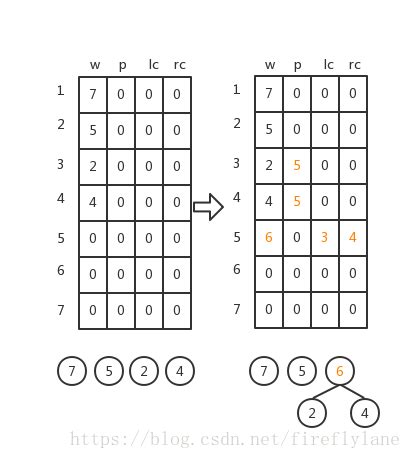
进行一下n-1次合并,依次产生n-1个结点HT[i],i=n+1…2n-1:
a)在HT[1…i-1]中选两个未被选中(从parent==0的结点中选)的weight最小的两个结点HT[s1]和HT[s2],s1,s2为两个最小结点下标;
b)修改HT[s1]和HT[s2]的parent值:HT[s1].parent=i;HT[s2].parent=i;
c)修改新产生的HT[i]:
- HT[i].weight=HT[s1].weight + HT[s2].weight;
- HT[i].lch=s1;HT[i].rch=s2
void CreatHuffmanTree (HuffmanTree HT,int n){
if(n<=1)return;
m=2*n-1;//数组共有2n-1个元素
HT=new HTNode[m+1];//0号单元未用,HT[m]表示根结点
for(i=0;i<=m;++i){//将2n-1个元素的lch,rch,parent置为0
HT[i].lch=0;
HT[i].rch=0;
HT[i].parent=0;
}
for(i=1;i<=n;++i)//输入前n个元素的weight
cin>>HT[i].weight;
for(i=n+1;i<=m;i++){
Select(HT,i-1;s1,s2);//在HT[k]中选择两个其双亲域为0,且权值最小的结点,并返回他们在HT中的序号s1和s2
HT[s1].parent=i;//表示从F中删除s1,s2
HT[s2].parent=i;
HT[i].lch=s1;
HT[i].rch=s2;
HT[i].weigth=HT[s1].weigth+HT[s2].weigth;
}
}
5.6.4哈夫曼编码
在远程通讯中,要将待传字符转换成由二进制表示的字符串:
若将编码设计为长度不等的二进制编码,即让待传字符串中出现次数较多的字符采用尽可能短的编码,则转换的二进制字符串便可能减少。
关键:要设计长度不等的编码,则必须使任一字符的编码都不是另一个字符的编码的前缀。——这种编码称做前缀编码。
问题:什么样的前缀码能使得电文总长最短?——哈夫曼编码
- 统计字符集中每个字符在电文中出现的平均概率(概率越大,要求编码越短)。
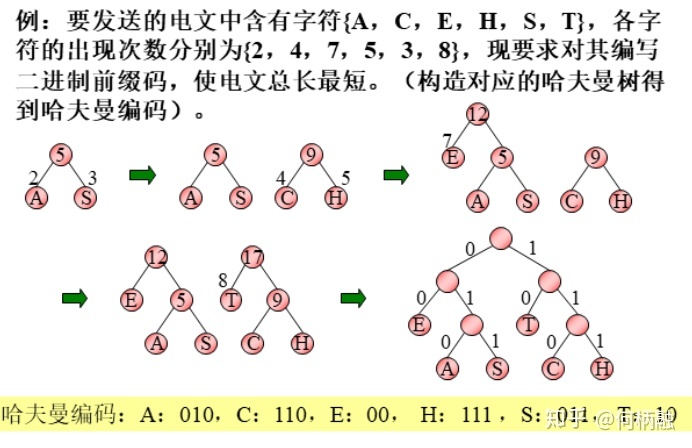
- 利用哈夫曼树的特点:权越大的叶子离根越近;将每个字符的概率值作为权值,构造哈夫曼树。则概率越大的结点,路径越短。
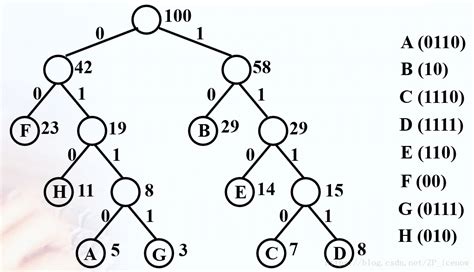
- 在哈夫曼树的每个分支上标上0或1:
- 结点的左分支标0,右分支标1
- 把从根到每个叶子的路径上的标号连接起来,作为该叶子代表的字符的编码。
两个问题:
为什么哈夫曼编码能够保证是前缀编码?
因为没有一片树叶是另一片树叶的祖先,所以每个叶节点的编码就不可能是其他叶节点编码的前缀。
为什么哈夫曼编码能够保证字符编码总长最短?
因为哈夫曼树的带权路径长度最短,故字符编码的总长最短。
哈夫曼编码的性质
- 性质1:哈夫曼编码是前缀码
- 性质2:哈夫曼编码是最优前缀码
5.6.5哈夫曼编码的算法实现

void CreatHuffmanCode(HuffmanTree HT,HuffmanCode &HC,int n){
//从叶子到根逆向求每个字符的哈夫曼编码,存储在编码表HC中
HC=new char*[n+1];//分配n个字符编码的头指针矢量
cd=new char [n];//分配临时存放编码的动态数组空间
cd[n-1]='\0';//编码结束符
for(i=1;i<=n;i++){//逐个字符求哈夫曼编码
start=n-1;
c=i;
f=HT[i].parent;
while(f!=0){//从叶子结点开始向上回溯,直到根结点
--start;//回溯一次start向前指一个位置
if(HT[f].lchild==c)cd[start]='0';//结点c是f的左孩子,则生成代码0
else cd[start]='1';//结点c是f的右孩子,则生成代码1
c=f;//继续向上回溯
f=HT[f].parent;
}
HC[i]=new char[n-start];//为第i个字符串编码分配空间
strcpy(HC[i],&cd[start]);//将求得的编码从临时空间cd复制到HC的当前行中
}
delete cd;
}
5.6.6文件的编码和解码
1、编码
① 输入各字符及其权值
② 构造哈夫曼树——HT[i]
③ 进行哈夫曼编码——HC[i]
④ 查HC[i],得到各字符的哈夫曼编码
2、解码
① 构造哈夫曼树
② 依次读入二进制码
③ 读入0,则走向左孩子;读入1,则走向右孩子
④ 一旦到达某叶子时,即可译出字符
⑤ 然后再从根出发继续译码,直到结束。