https://stackoverflow.com/questions/62067400/understanding-accumulated-gradients-in-pytorch

有一个小的计算图，两次前向梯度累积的结果，可以看到梯度是严格相等的。

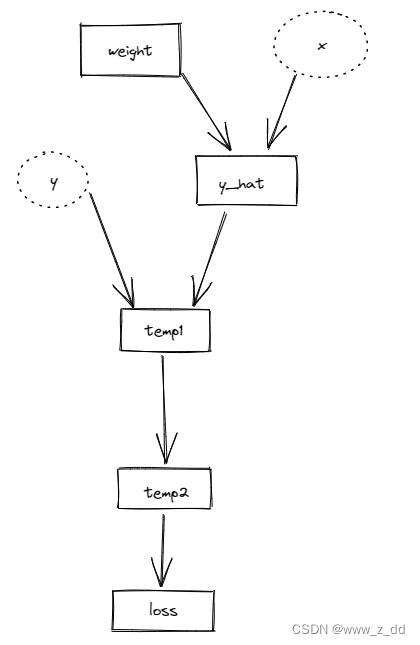
代码：

import numpy as np
import torch


class ExampleLinear(torch.nn.Module):

    def __init__(self):
        super().__init__()
        # Initialize the weight at 1
        self.weight = torch.nn.Parameter(torch.Tensor([1]).float(),
                                         requires_grad=True)

    def forward(self, x):
        return self.weight * x


model = ExampleLinear()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)


def calculate_loss(x: torch.Tensor) -> torch.Tensor:
    y = 2 * x
    y_hat = model(x)
    temp1 = (y - y_hat)
    temp2 = temp1**2
    return temp2


# With mulitple batches of size 1
batches = [torch.tensor([4.0]), torch.tensor([2.0])]

optimizer.zero_grad()
for i, batch in enumerate(batches):
    # The loss needs to be scaled, because the mean should be taken across the whole
    # dataset, which requires the loss to be divided by the number of batches.
    temp2 = calculate_loss(batch)
    loss = temp2 / len(batches)
    loss.backward()
    print(f"Batch size 1 (batch {i}) - grad: {model.weight.grad}")
    print(f"Batch size 1 (batch {i}) - weight: {model.weight}")
    print("="*50)

# Updating the model only after all batches
optimizer.step()
print(f"Batch size 1 (final) - grad: {model.weight.grad}")
print(f"Batch size 1 (final) - weight: {model.weight}")

运行结果

Batch size 1 (batch 0) - grad: tensor([-16.])
Batch size 1 (batch 0) - weight: Parameter containing:
tensor([1.], requires_grad=True)
==================================================
Batch size 1 (batch 1) - grad: tensor([-20.])
Batch size 1 (batch 1) - weight: Parameter containing:
tensor([1.], requires_grad=True)
==================================================
Batch size 1 (final) - grad: tensor([-20.])
Batch size 1 (final) - weight: Parameter containing:
tensor([1.2000], requires_grad=True)

然而，如果训练一个真实的模型，结果没有这么理想，比如训练一个bert，𝐵=8,𝑁=1：没有梯度累积（累积每一步），

𝐵=2,𝑁=4：梯度累积（每 4 步累积一次）
使用带有梯度累积的 Batch Normalization 通常效果不佳，原因很简单，因为 BatchNorm 统计数据无法累积。更好的解决方案是使用 Group Normalization 而不是 BatchNorm。
https://ai.stackexchange.com/questions/21972/what-is-the-relationship-between-gradient-accumulation-and-batch-size