熵(Entropy)是一个重要的概念,最初出现在热力学领域,用于描述系统的混乱程度或不确定性。熵也被广泛应用于信息理论、统计学和计算机科学等领域。通常来讲,熵,是对混乱程度、不确定程度的度量。熵越大,混乱程度、不确定程度越高。
一热力学中的熵
在热力学中,熵是一个衡量系统无序程度的物理量。熵的增加代表系统的无序性增加,而熵的减少则代表系统的有序性增加。热力学熵的概念可以简单地理解为系统能量的一种度量,它与能量的分布和微观状态的数量有关。
下面我们用一个例子来举例:
假设房间中只有四个空气分子,用不同颜色来标记这四个空气分子。这四个空气分子在房间中可能的情况全部列举如下:
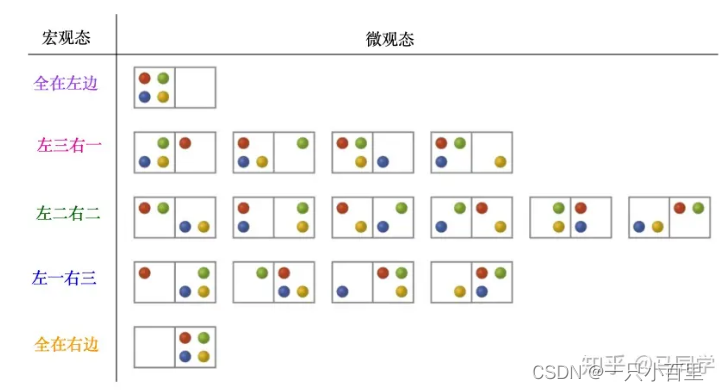
上图中,左边的文字称为“宏观态”,右边的分子分布状态称为“微观态”,比如宏观态“左二右二”,指的是房间左边有两个分子,右边也有两个分子,但是在微观上对应的是六种分子的分布,而总共有16种分子分布,所以宏观态“左二右二”发生的概率为:
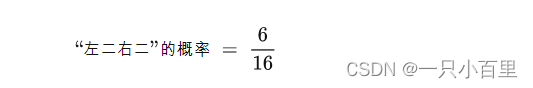
根据玻尔兹曼的观点,对于一个由N个微观粒子组成的系统,其熵(S)可以表示为:
S = k * ln(W)
(其中k为玻尔兹曼常数,该常数存在的意义,某种程度上是为了统一各种熵的定义的),而W是系统的微观状态数。
直观得出,熵值是正相关于微观态的个数的 ![]()
那么微观态个数最大的“左二右二”,也就是熵最大的宏观态。根据熵增原理,其它的宏观态都是
不稳定的(熵较小),会自发的变换为“左二右二”。

正如热水和冷水倒入一个容器中,最后温度会相同。
二.信息论中的熵
在信息理论中,熵用于衡量信息的不确定性或随机性,与热力学上的熵本质上是相同的。
信息论的创始人香农在其著作《通信的数学理论》中提出了建立在概率统计模型上的信息度量。他把信息定义为“用来消除不确定性的东西”。在信息世界,熵越高,则能传输越多的信息,熵越低,则意味着传输的信息越少。
信息熵的引入:
假设存在一只麦克斯韦恶魔,它能只让处于右半空间的蓝色分子进入左半空间,处于左半空间的红色分子进入右半空间。从而达到新的平衡,在新的状态,熵值为0,因为最后只存在
左边只有蓝色分子,右边只有红色分子这种情况。

那么减少的熵去哪里了?
这些熵以信息的形式进入恶魔的大脑中,这些信息包括分子的颜色,运动方向,位置等。当我们认为信息等价于熵时,这个系统的熵并没有减少。

在信息理论中,熵用于衡量随机变量的不确定性。对于一个离散随机变量X,其熵的计算公式为:
H(X) = -Σ(p(x) * log2(p(x)))
其中,H(X)表示X的熵,p(x)表示随机变量X取值为x的概率,log2表示以2为底的对数。
三.信息熵的性质
参考博客:“熵”详细学习笔记——什么是熵?有什么性质?联合熵等其他熵的作用_熵的特征变量是什么_yiyayiya980624的博客-CSDN博客