题目一：

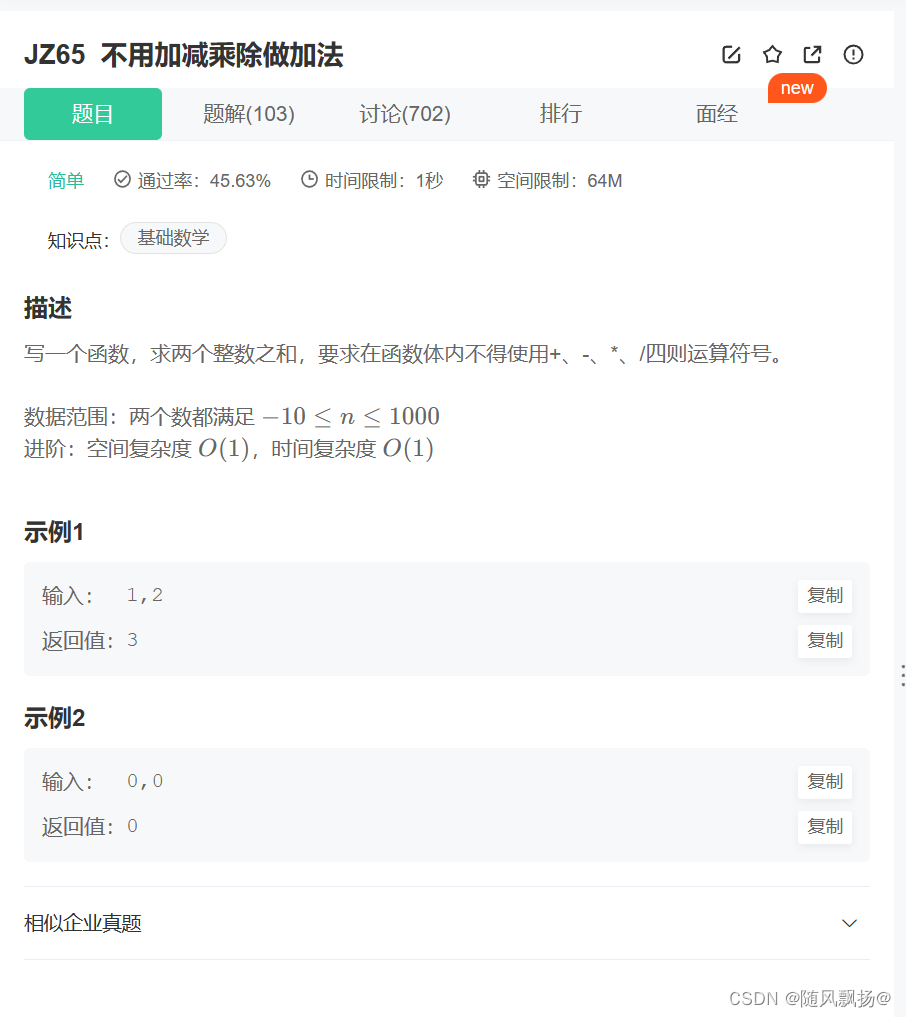
题目链接：

思路一：

1.两个数二进制之间进行异或如果不产生进位操作那么两个数的和就是就是两个数进行异或的结果。
举例：5（0101）2（0010）进行异或等于：7（0111）相同为0，不同位1.
2.如果两个数之间需要进位
1.如果两个1进行异或那么这个位置就变成了0满足进位的条件。（对于两个数异或求非进位和来说）。
2.只有两个1才是进位，所以使用与的方法获取要进的位之后进行左移动。（得到进位之后的数值）。
3.进行相加，但是不可以使用加法。因为我们知道两个数之间如果不产生进位操作，按位异或就是他们的和。
4.循环判断按位与的结果为0的时候说明两个数相加不存在进位。

int Add(int num1, int num2 ) {
    // write code here
    int sum, forward;
    do
    {
        //1.每一个位置相加，不产生进位(10(1010)+2(0010)-->8(1000)不进位)
        sum = num1^num2;
        //2.找到要加的进位数(10(1010)&2(0010)-->2(0010)<<1-->4(0100))
        forward = (num1&num2) << 1;
        //3.将前两步的值相加，但是相加不能用加法，重复前面两个步骤，直到不产生进位
        num1 = sum;
         //第二步的forward值为0，说明没有位需要前进，它们的和必然是sum的值
        num2 = forward;

    } while (num2 != 0);//结束条件是不产生进位

    return num1;
}

题目二

题目链接：

>思路一：

1.使用双for循环判断。
2.从1到n循环遍历，每一个数在数组中从前到后去判断。是否存在
3.如果数组被遍历完全动没有相等的值那么说明这个外面循环的这个数不存在于数组中。

int* findDisappearedNumbers(int* nums, int numsSize, int* returnSize){
    int n = numsSize;
    int* num = (int*)calloc(n,sizeof(int));
    int count = 0;
    int j = n;
    int flag = 0;
    for (int i = 1; i <= n; i++)
    {
        int j = 0;
        for (j = 0,flag=0; j < n; j++)
        {
            if ((nums[j])==i )
            {
                flag = 1;
                break;
            }
        }

        if (flag!=1)
        {
            (*(num+count)) = i;
            count++;
            flag = 0;
        }
    }

    (*returnSize) = count;
    return num;
}

产生问题：

>思路二：

0.进行快速排序使nums先有序
1.不允许开辟额外的空间，因为有连续的数值存在。
2.从nums找出单独的数放到num中，并记录个数为count。
3.把num的内容拷贝到nums中。num的前面count个元素置为空
4.这个时候满足[1,n]中存在的数只有一个在nums中。
5.从1到n开始遍历，nums数组。
6.当nums的最后一个不是n就需要有一个k<=n的一个判断条件如果没有的化（n2是nums中单个数的元素个数）[num[n2-1],n]这些数值是会失去找不到的。

int cmp(void*p1,void*p2)
 {
     return (*((int*)p1))-(*((int*)p2));
 }
int* findDisappearedNumbers(int* nums, int numsSize, int* returnSize){
    int n = numsSize;
    int* num = (int*)calloc(n,sizeof(int));
    int count = 0;
    qsort(nums,n,sizeof(int),cmp);
    //1.从前面到后面只有一个数按照顺序放到num里面。
    num[count]=nums[0];
    count++;
    for(int i=0;i<n-1;i++)
    {
        if(nums[i+1]!=num[count-1])
        {
            num[count]=nums[i+1];
            count++;
        }
    }

    //2.把只有一个的数放回去到nums中，把num置为空。
    int n2=count;
    count=0;
    memcpy(nums,num,sizeof(int)*n2);
    memset(num,0,sizeof(int)*n2);

    //3.当nums的最后一个不是n就需要有一个k<=n
    //的一个判断条件如果没有的化[num[n2-1],n]这些数值是会失去找不到的。
    int j=0;
    int k=1;
    //1,1,2,2,这样的情况。
    //1，2，有k<=n否则是否出现这样的情况导致有的数没有判断到。
    while(j<n2||k<=n)
    {
        if(nums[j]==k)
        {
            k++;
            j++;
        }
        else
        {
            num[count++]=k;
            k++;
        }
    }
    (*returnSize) = count;
    return num;
}