目录
前言
福利:文末有matlab全套资料哦
01分段函数
02复合图
⚪️ 两个一元函数y=x^3-x-1和y=|x|^(0.2)sin(5x)在区间-1<2的复合图。函数与图像<>
03三维平面图
⚪️ 三维平面图使用mesh绘制网格图,surf绘制三维曲面图,使用meshgrid生成三维网格矩阵,也就是区间变量值。
使用mesh进行绘制网格图
使用surf绘制曲面图
使用contour方法绘制等高线
如果确定某一等高线直接在后面添加参数
04三维线型图
⚪️ 三维线性图使用plot3函数,而二维使用plot
使用plot3绘制三维线条
05矩阵运算(线性方程组)
⚪️ 线性方程组、逆矩阵inv、特征值和特征向量eig、二次型矩阵代数
使用rref化为行最简单求方程组的解答
06非线性方程组
⚪️ 函数和方程非线性方程组变量不是一次的二次大于一次,这与线性方程组进行对比就能很清晰了
07函数的极值和零点
⚪️ "零点" 通常用于描述函数在 x 轴上的交点,也就是函数的值等于 0 的点。
08微积分
⚪️ 微积分是数学中的一个分支,主要研究函数的微分和积分微积分
导数(微分)
函数梯度
09符号对象
计算精度和数据类型转换
10符号矩阵和符号函数
符号矩阵
符号函数
前言
实践是检验知识和技能的唯一标准。只有将所学的知识应用到实际问题中,并通过实践不断地调整和完善,才能真正掌握和理解这些知识。
在 MATLAB 中,可以通过编写代码、运行程序、调试错误等方式进行实践。例如,可以尝试解决实际问题,如数据分析、信号处理、图像处理等,使用 MATLAB 中的函数和工具箱进行计算和处理。在实践中,可以深入理解 MATLAB 中的各种函数和工具,掌握它们的使用方法和注意事项,同时也可以发现其中的问题和不足,并通过实践不断地改进和完善。
福利:文末有matlab全套资料哦
01分段函数
⚪️ 函数f(x),当x>1,y=x^2;当x=[-1,1],y=1;当x<=-1,y=3+2x
第一种方法使用匿名函数的方法,就是使用不等号判断,当在此区间布尔值为1,对应函数乘以此布尔值不等于0.
% 方法1
% 定义分段函数
f = @(x) (x > 1) .* x.^2 + (-1 <= x & x < 1) .* 1 + (x <= -1) .* (3 + 2*x);
% 生成 x 向量
x = linspace(-2, 2, 1000);
% 计算 y 向量
y = f(x);
% 绘制函数曲线
plot(x, y);
grid on;
xlabel('x');
ylabel('y');
title('分段函数 f(x)');
另一种方法就是用常规函数进行,先定义分段函数part,用n统计其长度,可以把n当作x和y值对应的下标,生成x向量传入到函数part生成y值,通过plot绘制图形
part.m
% 定义分段函数
function y = part(x)
n = length(x);
for i = 1:n
if x(i)>1
y(i)=x(i).^2;
elseif x(i)>-1
y(i)=1;
else
y(i)=3+2*x(i);
end
end
end主函数
% 生成 x 向量
x = linspace(-2, 2, 1000);
% 计算 y 向量
y = part(x);
% 绘制函数曲线
plot(x, y);
grid on;
xlabel('x');
ylabel('y');
title('分段函数 f(x)');或者使用find获取下标,方法和上述第二个方法类似,都是找下标的方式
% 生成 x 向量
x = linspace(-2, 2, 1000);
% 计算 y 向量
y = zeros(size(x)); % 初始化 y 向量
ind1 = find(x > 1); % 第一段函数的下标
ind2 = find(x > -1 & x <= 1); % 第二段函数的下标
ind3 = find(x <= -1); % 第三段函数的下标
y(ind1) = x(ind1).^2; % 第一段函数
y(ind2) = 1; % 第二段函数
y(ind3) = 3 + 2*x(ind3); % 第三段函数
% 绘制函数曲线
plot(x, y);
grid on;
xlabel('x');
ylabel('y');
title('分段函数 f(x)');02复合图
⚪️ 两个一元函数y=x^3-x-1和y=|x|^(0.2)sin(5x)在区间-1<x<2的复合图。函数与图像
使用hold on方法将在同一个图像上进行绘制
% 生成 x 向量
x = linspace(-1, 2, 1000);
% 计算 y1 向量
y1 = x.^3 - x - 1;
% 计算 y2 向量
y2 = abs(x).^0.2 .* sin(5*x);
% 绘制函数曲线
plot(x, y1, 'Color','r','LineWidth', 2);
hold on; % 将两个曲线绘制在同一张图上
plot(x, y2, 'LineWidth', 2);
grid on;
xlabel('x');
ylabel('y');
title('两个一元函数复合图');
% 图例
legend('y=x^3-x-1', 'y=|x|^{0.2}sin(5x)');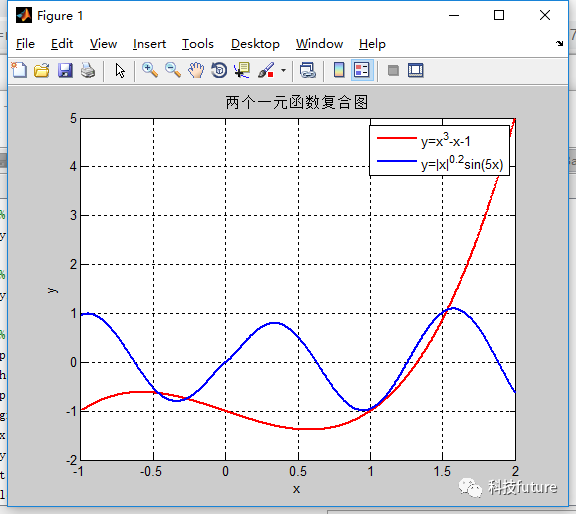
除了使用上述的plot方法还可以使用fplot匿名函数方法进行绘制,fplot仅针对一元函数,二元函数不能使用的一种方法。
% 定义匿名函数
f = @(x) x^3-x-1;
y = @(x) abs(x).^0.2.*sin(5*x);
% 绘制函数曲线
fplot(f,[-1,2],'r-.');
hold on;
fplot(y,[-1,2]);
hold off
% 添加网格;
grid on
% 添加坐标轴标签和标题
xlabel('x');
ylabel('y');
title('两个一元函数复合图');
% 添加图例
legend('y=x^3-x-1', 'y=|x|^{0.2}sin(5x)');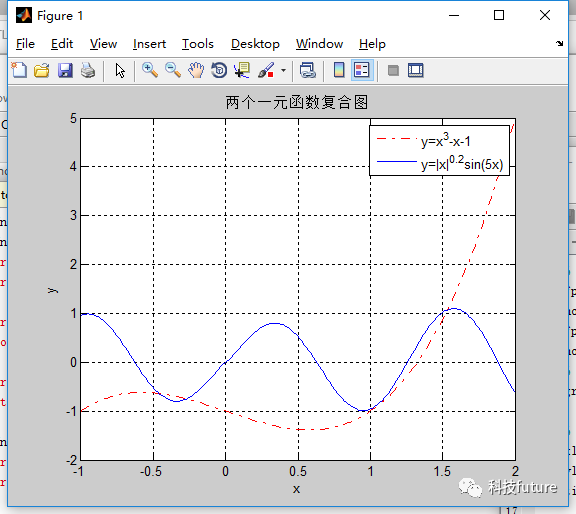
03三维平面图
⚪️ 三维平面图使用mesh绘制网格图,surf绘制三维曲面图,使用meshgrid生成三维网格矩阵,也就是区间变量值。
使用mesh进行绘制网格图
clear all; % 清除全部变量
clc; % 清屏
% 生成数据
% meshgrid 函数可以用于生成二维网格矩阵,从而方便地生成网格图或三维图形。
[X, Y] = meshgrid(-2:0.1:2); % 相当于生成区间
%三维表达式
Z = X.^2 - Y.^2;
% mesh方法绘制三维网格图
mesh(X, Y, Z);
xlabel('x');
ylabel('y');
zlabel('z');
title('三维网格图');
使用surf绘制曲面图
clear all; % 清除全部变量
clc; % 清屏
% 生成数据
% meshgrid 函数可以用于生成二维网格矩阵,从而方便地生成网格图或三维图形。
[X, Y] = meshgrid(-2:0.1:2); % 相当于生成区间
%三维表达式
Z = X.^2 - Y.^2;
% surf方法绘制三维曲面图
surf(X, Y, Z);
xlabel('x');
ylabel('y');
zlabel('z');
title('三维曲面图');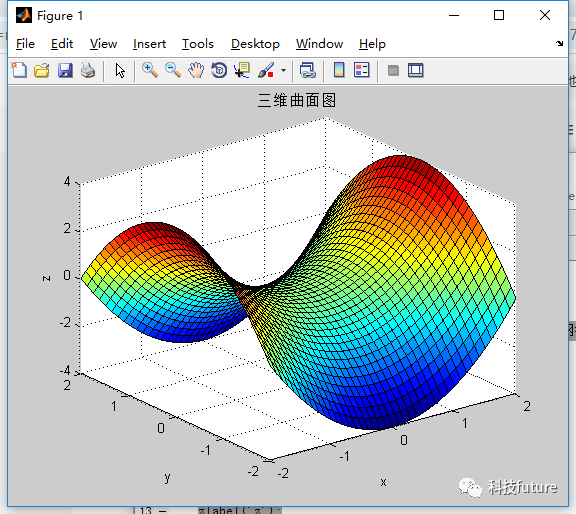
使用contour方法绘制等高线
clear all; % 清除全部变量
clc; % 清屏
% 生成数据
% meshgrid 函数可以用于生成二维网格矩阵,从而方便地生成网格图或三维图形。
[X, Y] = meshgrid(-2:0.1:2); % 相当于生成区间
%三维表达式
Z = X.^2 - Y.^2;
% contour方法绘制三维等高线
contour(X, Y, Z);
xlabel('x');
ylabel('y');
zlabel('z');
title('三维等高线');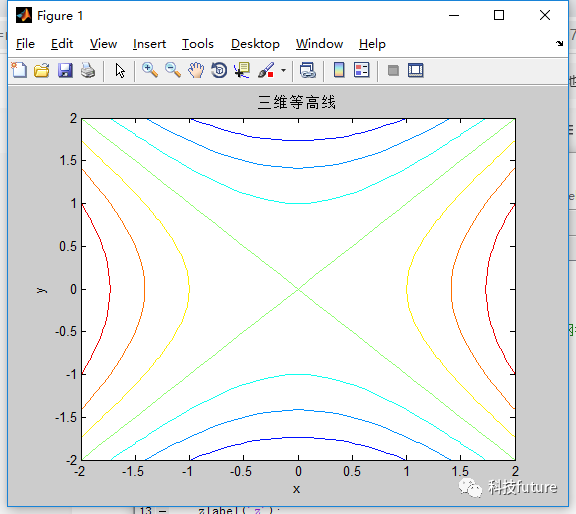
如果确定某一等高线直接在后面添加参数
clear all; % 清除全部变量
clc; % 清屏
% 生成数据
% meshgrid 函数可以用于生成二维网格矩阵,从而方便地生成网格图或三维图形。
[X, Y] = meshgrid(-2:0.1:2); % 相当于生成区间
%三维表达式
Z = X.^2 - Y.^2;
% contour方法绘制等高线
contour(X, Y, Z,[1]);
xlabel('x');
ylabel('y');
zlabel('z');
title('等高线为1');
legend('等高线')
04三维线型图
⚪️ 三维线性图使用plot3函数,而二维使用plot
使用plot3绘制三维线条
% 生成数据
t = linspace(0, 10*pi, 1000);
x = sin(t);
y = cos(t);
z = t;
% 绘制三维线条图
plot3(x, y, z);
xlabel('x');
ylabel('y');
zlabel('z');
title('三维线条图');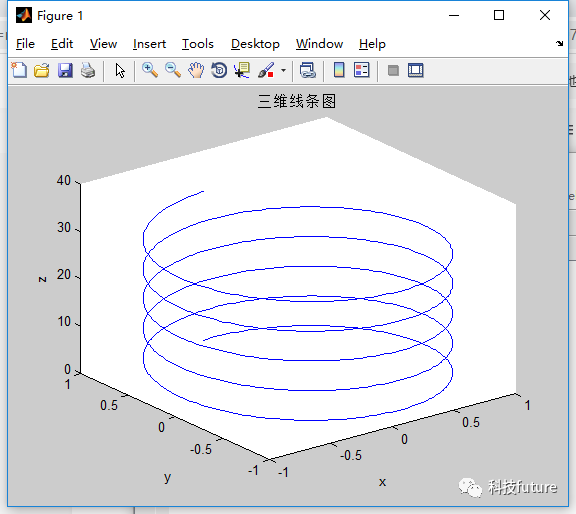
05矩阵运算(线性方程组)
⚪️ 线性方程组、逆矩阵inv、特征值和特征向量eig、二次型矩阵代数
使用rref化为行最简单求方程组的解答

clear all;
%根据线性方程组得矩阵A和b
A = [1 -1 1 -1;-1 1 1 -1;2 -2 -1 1];
b = [1;1;-1];
% 只有当矩阵A的秩和增广矩阵(A,b)秩相等才有解答
if rank(A)==rank([A,b])
%使用rref求增广矩阵行最简
rref([A,b])
else
disp('此方程组无解')
end输出结果:
ans =
1 -1 0 0 0
0 0 1 -1 1
0 0 0 0 0
矩阵里有求二次型问题,在求二次型的过程中也少不了求特征值和特征向量的过程

首先根据给出的公式写出矩阵A,通过矩阵A求特征值和特征向量,正交化,规范化然后求出标准化。我的matlab版本较低,所以自行定义正交化,规范化函数
normalize.m
function V_norm = normalize(V) %定义规范化函数
% 对向量进行规范化
[m, n] = size(V);
V_norm = zeros(m, n);
for i = 1:n
V_norm(:, i) = V(:, i)/norm(V(:, i));
end
endgramSchmidt.m
function [Q, R] = gramSchmidt(A)
% Gram-Schmidt正交化过程
[m, n] = size(A);
Q = A;
R = zeros(n, n);
for j = 1:n
R(j, j) = norm(Q(:, j));
Q(:, j) = Q(:, j)/R(j, j);
for i = j+1:n
R(j, i) = Q(:, j)'*Q(:, i);
Q(:, i) = Q(:, i) - R(j, i)*Q(:, j);
end
end
end主函数:
% 根据式子写二次型的矩阵A
A =[1 -2 2;-2 -2 4;2 4 -2];
% 求A的特征值和特征向量
[V,D]=eig(A);
% 特征向量的正交化
U = gramSchmidt(V);
%特征向量的规范化
Q = normalize(U);
%最后得到标准型
S = Q'*A*Q输出结果:
S =-7.0000 0.0000 0.00000.0000 2.0000 00.0000 -0.0000 2.0000
06非线性方程组
⚪️ 函数和方程非线性方程组变量不是一次的二次大于一次,这与线性方程组进行对比就能很清晰了

% 定义非线性方程组f = @(x) [9*x(1)^2 + 36*x(2)^2 + 4*x(3)^2 - 36; x(1)^2 - 2*x(2)^2 - 20*x(3); 16*x(1) - x(1)^3 - 2*x(2)^2 - 16*x(3)^2];% 初始值x0 = [1; 1;1];% 求解方程组x = fsolve(f, x0);% 输出结果disp(x);
输出结果:
0.13420.9972-0.0985
07函数的极值和零点
⚪️ "零点" 通常用于描述函数在 x 轴上的交点,也就是函数的值等于 0 的点。
一个函数可能有多个零点,也可能没有零点。fzero 函数用于求解函数的零点。"求根" 通常用于描述解方程的过程,也就是找到一个或多个方程的根。对于一个方程 $f(x) = 0$,求根就是要找到它的解 x,使得 f(x) = 0。一个方程可能有多个根,也可能没有根。fsolve 函数用于求解方程的根。在数学中,极值是函数在某一区间内的最大值或最小值,也称为局部极值。
在 MATLAB 中,可以使用 fminbnd 和 fminsearch 函数找到函数的局部最小值。
求根

这里只求最后一个,其他同理
% 函数表达式f =(2.*x+3).^3-4% 使用conv展开f_v = expand(f) % 8*x^3 + 36*x^2 + 54*x + 23% 展开后提取系数求根p = [8,36,54,23]value = roots(p)% 验证polyval(多项式系数列表,代入的值)polyval(p,value)
输出结果:
value =-1.8969 + 0.6874i-1.8969 - 0.6874i-0.7063ans =1.0e-13 *0.1066 + 0.0799i0.1066 - 0.0799i0.0355
或者用fzero,需要指定区间
% 函数表达式f =@(x)(2.*x+3).^3-4% 区间x0 = [-3,3]% 求解方程的零点x = fzero(f, x0);% 输出结果disp(x);
fzero 函数用于求解单变量非线性方程的零点,即在给定区间内找到函数的一个根。它使用的是单点迭代法(也称作牛顿迭代法),通过不断逼近函数的零点来计算方程的解。因此,fzero 函数适用于求解单变量非线性方程的根,但不能用于求解多变量非线性方程组的根。
roots 函数则用于求解多项式方程的根,即找到多项式在复数域中的所有根。它的输入是一个包含多项式系数的向量,输出是一个包含多项式在复数域中所有根的向量。roots 函数使用的是拉格朗日-牛顿插值法,通过对多项式进行插值来计算多项式的根。因此,roots 函数适用于求解多项式方程的根,但不能用于求解非多项式方程的根。
极值
`fminbnd` 是 MATLAB 中用于求解单变量有界函数最小值的函数,它可以在指定的区间内自动寻找一个函数的最小值点。`fminbnd` 函数的基本语法如下:
[x, fval] = fminbnd(fun, x1, x2)其中,`fun` 表示待求解的单变量有界函数,可以是一个函数句柄、一个匿名函数或一个函数字符串;`x1` 和 `x2` 分别表示待求解区间的左右端点,即函数的取值范围。函数的输出结果包括一个标量 `x`,表示函数的最小值点,以及一个标量 `fval`,表示函数在最小值点的取值。
需要注意的是,`fminbnd` 函数使用的是黄金分割法(golden section method),通过不断狭窄区间范围来逐步逼近函数的最小值点。因此,`fminbnd` 函数适用于求解单变量有界函数的最小值,但不能用于求解多变量函数的最小值、无界函数的最小值或非连续函数的最小值。
下面是一个使用 `fminbnd` 函数求解函数最小值的简单例子:
% 定义一个函数fun = @(x) x.^2 - 2*x + 1;% 求解函数的最小值x1 = 0; % 区间x2 = 2; % 区间[x, fval] = fminbnd(fun, x1, x2);% 输出结果disp(x); %坐标xdisp(fval); %坐标y
在上述代码中,我们定义了一个函数 `fun`,它表示函数 f(x)=x^2-2x+1。然后,我们使用 `fminbnd` 函数求解该函数在区间 [0,2]内的最小值点。需要注意的是,为了确保函数的最小值在指定区间内,需要根据具体的问题选择合适的区间范围,并进行必要的验证和调整,以保证求解结果的准确性和稳定性。与fminbnd相似的是fminsearch解决多元函数极值问题,函数的参数相似,第一个是多元函数表达式,第二个是指定区间。
08微积分
⚪️ 微积分是数学中的一个分支,主要研究函数的微分和积分微积分
导数(微分)

%定义符号变量tsyms tx = log(cos(t));y = cos(t)-t.*sin(t);%x对t求导数,求导1次dx_dt = diff(x,t)%y对t求导数,求导1次dy_dt = diff(y,t)% 求方程的解,当x=-1的时候t等于多少% 使用符号函数solve进行解答% t的区间在[0,1.5]大于零x=log(cos(t))==-1;tt = abs(solve(x,t))%代入到方程中,subs(函数,旧变量,新变量)dx_dt = subs(dx_dt,t,tt)dy_dt = subs(dy_dt,t,tt)%最后得数,符号函数转换为具体的值用evaleval(dx_dt./dy_dt)
最后输出:
dx_dt =-sin(t)/cos(t)dy_dt =- 2*sin(t) - t*cos(t)tt =acos(exp(-1))acos(exp(-1))dx_dt =-exp(1)*(1 - exp(-2))^(1/2)-exp(1)*(1 - exp(-2))^(1/2)dy_dt =- 2*(1 - exp(-2))^(1/2) - exp(-1)*acos(exp(-1))- 2*(1 - exp(-2))^(1/2) - exp(-1)*acos(exp(-1))ans =1.09951.0995
积分

%被积函数表达式f= @(x) exp(2.*x).*cos(x).^3;% 积分方式一disp('integral方法');Q1 = integral(f, 0, 2*pi)%积分方式2disp('quad方法');Q2 = quad(f, 0, 2*pi)
输出结果:
integral方法Q1 =9.7054e+04quad方法Q2 =9.7054e+04
函数梯度
在数学中,梯度是一个向量,它的方向与函数值增加最快的方向相同,大小表示函数值增加最快的速率。在 MATLAB 中,可以使用符号工具箱和数值工具箱计算函数的梯度。
使用符号工具箱,可以对符号表达式进行梯度计算。可以使用 `gradient` 函数计算符号表达式的梯度向量。以下是一个示例代码,使用符号工具箱计算函数 f(x,y)=x^2+y^2$ 在点 (1,2)$处的梯度向量:
% 定义符号变量和函数syms x y;f = x^2 + y^2;% 计算梯度grad_f = gradient(f, [x, y]);% 在点 (1,2) 处计算梯度向量x0 = 1;y0 = 2;grad_f_val = subs(grad_f, [x, y], [x0, y0]);% 输出结果[2,4]disp([grad_f_val]) % 2 4
在这个代码中,我们首先定义了符号变量 `x` 和 `y`,以及函数 f(x,y)=x^2+y^2。然后,我们使用 `gradient` 函数计算了函数的梯度向量。最后,我们在点 (1,2) 处计算了梯度向量,并输出了结果。运行这个代码,可以得到函数 f(x,y)=x^2+y^2在点 (1,2) 处的梯度向量为 [2, 4]。
09符号对象
⚪️ 符号运算使用--种特殊的数据类型,称为符号对象(SymbolicObject),用字
符串形式表达,但又不同于字符串( Char Array).符号运算中的变量、函数和表达式都是符号对象.

% 这是数值表达式n = pi^2% 数值转化为符号对象a = sym(n)% 定义符号变量以及符号计算表达式syms x y cd = x^3+2*y^2;% 定义符号矩阵A = [x,y;2*x,2*y]% 符号变量x用符号c替代A = subs(A,x,c)
从上面可以看出万物皆可符号,定义单个符号使用sym,多个使用syms
计算精度和数据类型转换
符号数值计算默认精度为32位十进制,是MATLAB数值计算的两倍,符号工具箱还提供了计算精度设置指令,可以定义任意精度的数值计算."vpa" 是 MATLAB 中的一个函数,它的全称是 "Variable Precision Arithmetic",中文翻译为"可变精度算术"。该函数可以用来进行高精度计算,避免由于浮点数运算带来的舍入误差。

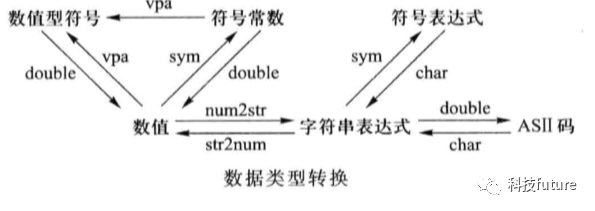
% s为圆周率s=pi% 将数值计算精度设置为8位digits(8)% 求s的数值结果x=vpa(s)% 采用n位计算精度求s的数值结果x=vpa(s,n)%符号对象转换为双精度double(s)%符号对象转换为字符串char(s)
输出结果:
s =
3.1416
x =
3.1415927
x =
3.141592654
ans =
3.1416
ans =c10符号矩阵和符号函数
⚪️ MATLAB大部分矩阵和数组运算符及指令都可以应用于符号矩阵,大部分MATLAB数学函数和逻辑关系运算也可用于符号对象.另外还有

符号矩阵
clear;% 符号矩阵AA = sym('[a,b;c,d]');% B为A矩阵的逆B = inv(A)% 矩阵的运算A./BB.\AA/BB\A% 求符号矩阵的特征值和特征向量eig(A)
输出结果:
B =[ d/(a*d - b*c), -b/(a*d - b*c)][ -c/(a*d - b*c), a/(a*d - b*c)]ans =[ (a*(a*d - b*c))/d, b*c - a*d][ b*c - a*d, (d*(a*d - b*c))/a]ans =[ (a*(a*d - b*c))/d, b*c - a*d][ b*c - a*d, (d*(a*d - b*c))/a]ans =[ a^2 + b*c, b*(a + d)][ c*(a + d), d^2 + b*c]ans =[ a^2 + b*c, b*(a + d)][ c*(a + d), d^2 + b*c]ans =a/2 + d/2 - (a^2 - 2*a*d + d^2 + 4*b*c)^(1/2)/2a/2 + d/2 + (a^2 - 2*a*d + d^2 + 4*b*c)^(1/2)/2
符号函数
% f(x,y)=(x-y)^3% g(x,y)=(x+y)^3% 定义符号变量syms x y;%定义函数f=(x-y)^3;g=(x+y)^3;%两个函数相乘h = f*g%展开多项式hs = expand(h)% 因式分解hf = factor(hs)%定义符号函数,自变量是x,yfun = symfun(f*g,[x,y])%符号计算替换无需使用subs方法s = fun(x,x^2+x+1)%合并同类项,变量xscol = collect(s,x)%化简ssim = simplify(scol)%最简形式ssim =simple(scol)% 数学公式的Latex输出latex(ssim)% 数学公式的C语言代码ccode(ssim)% 数学公式的matlab匿名函数代码
输出结果:
h =(x + y)^3*(x - y)^3hs =x^6 - 3*x^4*y^2 + 3*x^2*y^4 - y^6hf =(x - y)^3*(x + y)^3fun(x, y) =(x + y)^3*(x - y)^3s =-(x^2 + 1)^3*(x^2 + 2*x + 1)^3scol =- x^12 - 6*x^11 - 18*x^10 - 38*x^9 - 63*x^8 - 84*x^7 - 92*x^6 - 84*x^5 - 63*x^4 - 38*x^3 - 18*x^2 - 6*x - 1ssim =-(x^2 + 1)^3*(x + 1)^6ssim =-(x^2 + 1)^3*(x + 1)^6ans =- {\left(x^2 + 1\right)}^3\, {\left(x + 1\right)}^6ans =t0 = -pow(x*x+1.0,3.0)*pow(x+1.0,6.0);ans =@(x)-(x.^2+1.0).^3.*(x+1.0).^6
符号微积分
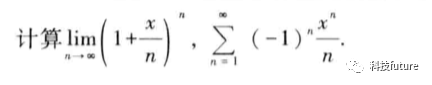
% 定义符号变量syms n x;%定义表达式f = (1+x/n)^n;g = (-1)^n*x^n/n;% 符号极限的计算,变量n趋于无穷limit(f,n,inf)% 离散求和,变量n从1到无穷symsum(g,n,1,inf)
计算结果:
ans =
exp(x)
ans =
piecewise([x == -1, Inf], [abs(x) <= 1 and x ~= -1, -log(x + 1)])从上述的几个例子可以看出,符号表达式在应用的时候更加的随意,之前的函数方法都没有变,变的是函数的表达式通过符号的形式进行表达,而不是变量,符号可以不用赋予具体的值就可以通过符号进行运算,而变量在最后是需要赋予具体的值才可以进行运算。
看到这篇文章
的人,2023兔年一定暴富,心想事成,爱情家庭事业都会大丰收!多吃不长肥肉,亲朋好友平安健康幸福快乐,而你心想事成,给俺点赞收藏起来,你的三连是我创作的动力哟!
充电君会在第一时间给你带来最新、最全面的解读,别忘了三联一波哦。
关注公众号:资源充电吧
回复:Chat GPT
充电君发你:免费畅享使用中文版哦
点击小卡片关注下,回复:IT
想要的资料全都有