机器学习(Regression:Case Study)
前言:
学习资料
| video | ppt | blog |
|---|
Example Application

建立一个model,将宝可梦的一些数据作为输入,然后输出宝可梦进化以后的战斗力CP值,这个model的建立尤为重要,但是这个模型的建立也是需要一步一步慢慢进行,下面,我们先从最简单的一个参数开始,然后到后面的多参数。
Step 1:Model
建立模型,我们建立一个Linear model(线性模型):
y = b + w * x
w and b are parameters(can be any value)
A set of function(一系列的函数)
f1: y = 10.0 + 9.0 ∙ xcp
f2: y = 9.8 + 9.2 ∙ xcp
f3: y = - 0.8 - 1.2 ∙ xcp
Step 2:Goodness of Function
我们有一系列的函数,但是这些函数哪一个是最好的,也就是说哪一个参数是最适合作为我们当前的预测模型,所以此时我们引入了损失函数(Loss Function)L
Loss Function:
函数的函数,用来评价模型函数的好坏,在这模型里面,我们可以通过转化,将该损失函数幻化为关于w和b的函数,我们此处用的是均方误差(MSE),定义不完全一样,但是基本的原理是一样的,取平方主要是为了防止正负误差相抵消,造成错误的拟合
各种误差可以了解这篇文章

| Loss Function L | 函数的函数 |
|---|---|
| input | a function |
| output | how bad it is |
通过将预测数据的函数带入L,我们可以得到一个关于w和b的函数
可以看作这是一个三维函数,输入数据有两种,颜色的深浅表示第三个维度
Step 3:Best Function
前面我们说明了损失函数的作用,接下来我们就应该学习如何找到最优的模型函数,即最优的w和b
损失函数的值肯定是越小越好,但是如何找到最小的值
下面是使用线性代数的知识进行解决,但是我看不懂(因为线性代数是一年前学的😢)

下面我们来讲解一种新的思路:梯度下降法,很容易理解
只考虑一个参数
单变量:(这里靠的是w,所以可以把b看作一个定值)
我们应该调整w找到最低点,高中的时候学过导数,导数为正,表示增加,w应该减少,导数为负,表示减少,w应该增加,导数的绝对值大小表示了此处的陡峭程度。
所以L关于w求导,然后随机选取一点w开始,接着对其进行变化更新,但是变化多少得由我们自己设定,导数也决定了增加还是减少
**Learn Rate:(学习率)**通过学习率的设定,我们可以很好的控制w的变化速度,设定过大,导致跳过最优解,过小,导致收敛过慢。
迭代更新,找到最优的函数对应的w

多参数
计算偏导,选取初始的w和b,然后使用上面的方法同时对他们进行更新

循环迭代,找到最优解

梯度
有兴趣的可以去了解一下这个概念,不是很好理解,但是很重要
等高线的法线方向

- Each time we update the parameters, we obtain
fthat makes 𝐿fsmaller.
How’s the results?
我们找到了当前函数集合里面的最优函数,但是这个函数具体的好坏我们很难评价,通过图像可以看出很多点无法进行拟合
Average Error:体现我们对未来预测数据的准确程度,是很重要的一个指标

优化方法,通过观察发现,将各个点连接起来以后更像一个曲线,那么我们可以试一下二次方差,或者高次方程
效果如下:

此时你会发现,并不是越高次的拟合效果越好,所以就引出了
Overfitting
training data的Average Error越来越小,但是Test data的表现却不尽如人意,甚至在五次方程时,大大超出了我们的预估,那么这种现象就叫做overfitting。因为我们前说过要让test data的Average Error越小越好

这种情况我们又该如何解决呢?
Redesign the Model
Back To Step 1
What are the hidden factors?

不同的宝可梦,可以用同一个公式进行估计吗?
答案肯定是不行,但是我们最后是用一个函数进行预测,所以我们需要进行统一
下面的图片展示的不是很清晰,实际上就是把多个函数进行柔和,但是每个函数需要乘以一个式子,那便是对输入数据的不同而进行设置,如果输入的是皮卡丘,我们就吧皮卡丘函数的式子设置为1,其他为0,那么就可以实现一个函数进行所有的预测。

Are there any otherhidden factors?

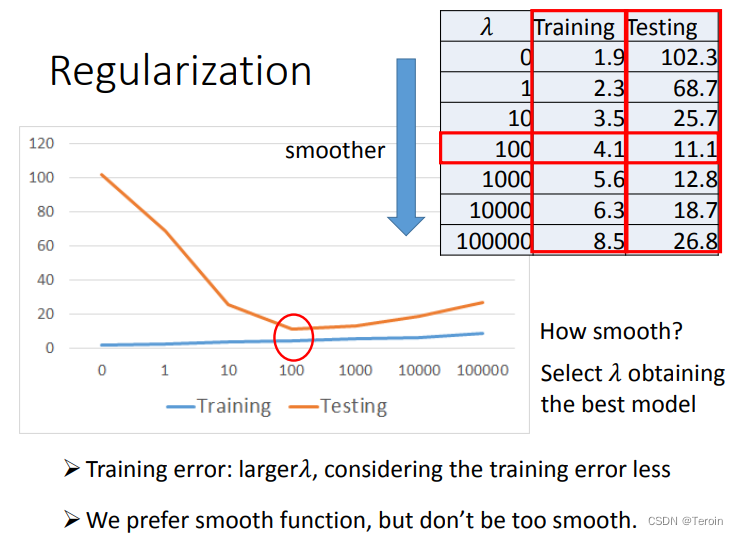
Regularization
Back To Step 2
这里我们分析两句话
- We believe smoother function is more likely to be correct?
在使用损失函数的时候,我们用的是train_data进行训练,调整参数,但是我们更关注的是test_data的预测情况,那么我们希望我们训练出来的函数是平滑的,那样在输入变化的时候,输出不会有很大的变化,从而减小我们预测的误差,所以这就要求我们在计算损失函数时关注w,防止正负影响,加上平方,但是w在里面的占比,我们可以手动调控,这样才能让损失函数最小的时候,我们对于test_data的预测情况更加准确,而我们进行调控的因子就是λ- Do you have to apply regularization on bias?
b只会是我们的函数上下平移,对于函数的平滑程度没有任何影响,所以不需要考虑在内