前言

• 本文关注在Pytorch中如何计算困惑度（ppl）
• 为什么能用模型 loss 代表 ppl

如何计算

当给定一个分词后的序列 $X=(x_0,x_1,\dots ,x_t)$, ppl 计算公式为：

• 其中 $p_{\theta }(x_i|x_{<i})$ 是基于 $i$ 前面的序列，第 $i$ 个 token 的 log-likelihood

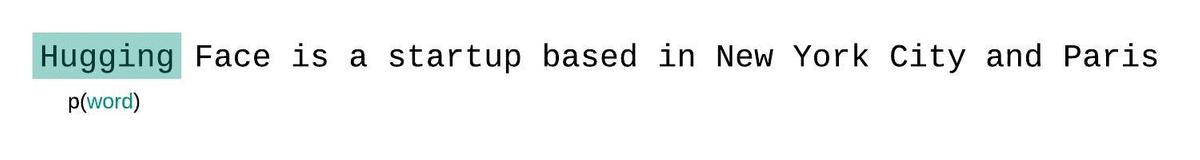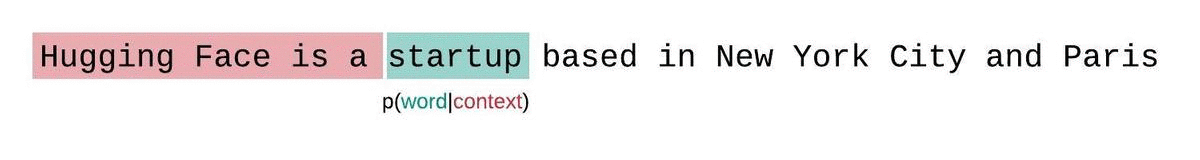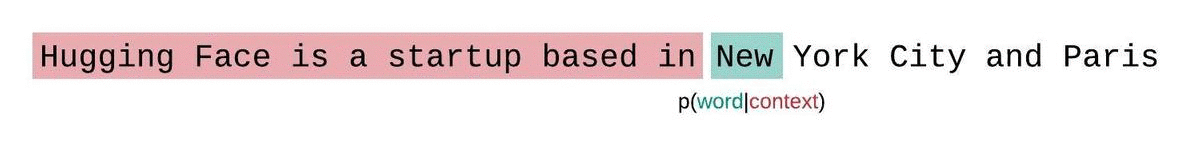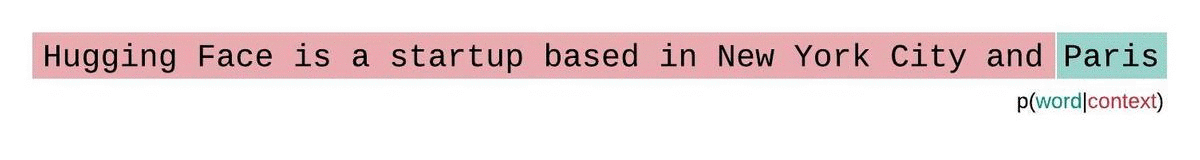
import torch
from tqdm import tqdm

max_length = model.config.n_positions
stride = 512
seq_len = encodings.input_ids.size(1)

nlls = []
prev_end_loc = 0
for begin_loc in tqdm(range(0, seq_len, stride)):
    end_loc = min(begin_loc + max_length, seq_len)
    trg_len = end_loc - prev_end_loc  # may be different from stride on last loop
    input_ids = encodings.input_ids[:, begin_loc:end_loc].to(device)
    target_ids = input_ids.clone()
    target_ids[:, :-trg_len] = -100

    with torch.no_grad():
        outputs = model(input_ids, labels=target_ids)

        # loss is calculated using CrossEntropyLoss which averages over valid labels
        # N.B. the model only calculates loss over trg_len - 1 labels, because it internally shifts the labels
        # to the left by 1.
        neg_log_likelihood = outputs.loss

    nlls.append(neg_log_likelihood)

    prev_end_loc = end_loc
    if end_loc == seq_len:
        break

ppl = torch.exp(torch.stack(nlls).mean())

这里我们可以看到 neg_log_likelihood = output.loss，这说明我们利用模型输出的 CrossEntropyLoss 就能代表 ppl。

为什么

交叉熵损失函数公式（pytorch中并不是直接按照此公式计算，还做了其他处理）

• 其中 $y$ 是真实 ground-truth 标签
• $\hat{y}$ 是模型预测的标签
• $C$ 是类别数目，这里可以看做vocabulary大小

在生成任务中，因为每个 $y_i$ 中只有一个位置是1，其余位置都是 0，其实上述公式也就是 $-log(y_i)$， 那么对一个序列 $X$，我们对每个token的 cross-entropy loss进行平均，其实就是 KaTeX parse error: {equation} can be used only in display mode.，也就是 ppl。因此在实际计算中，我们利用 cross-entropy loss 来代表一个句子的 ppl

参考：Perplexity of fixed-length models (huggingface.co)