1 主要内容

该程序基本复现《基于峰谷分时电价引导下的电动汽车充电负荷优化》，代码主要做的是基于NSGA-II的电动汽车充电负荷优化，首先，在研究电动汽车用户充电需求的前提下，利用蒙特卡洛方法对２种不同充电方式进行模拟并对其进行分析；分析用户响应度对电动汽车有序充电的影响，建立峰谷分时电价对电动汽车负荷影响的模型，在模拟出电动汽车无序充电负荷的基础上，用实际案例对模型进行验证，利用多目标遗传优化算法进行求解，验证峰谷分时电价对电网负荷优化的有效性。

该程序主要分成两部分，第一部分是峰谷电价优化部分，第二部分通过确定的峰谷平电价观测电动汽车充电负荷变化情况。

峰谷电价优化

程序采用NSGA-II算法，该算法是非常成熟、常用的多目标求解算法，是遗传算法的一种，作为智能优化算法，最关键的点是找到程序的输入和输出，剩下的即是采用算法进行连接即可，在该程序中，输入是分时电价作为变量，输出是两个目标，分别是负荷均方差最小和电动汽车用户充电费用最小。

目标1：

目标2：

优化结果：

对于帕累托多目标而言，会存在多组运行结果，即多个自变量+目标函数的组合，求解此类问题的帕累托最优解有以下常用的几种方法：权重系数变换法，给每个子目标函数赋予权重系数后转变为单目标优化问题；并列选择法，将群体所有个体按照子目标函数划分子群体，各自选出适应度高的个体以得到新的子群体，再将其合并，不断进行至最大次数，最终得到多目标优化的帕累托最优解。

电动汽车充电负荷变化

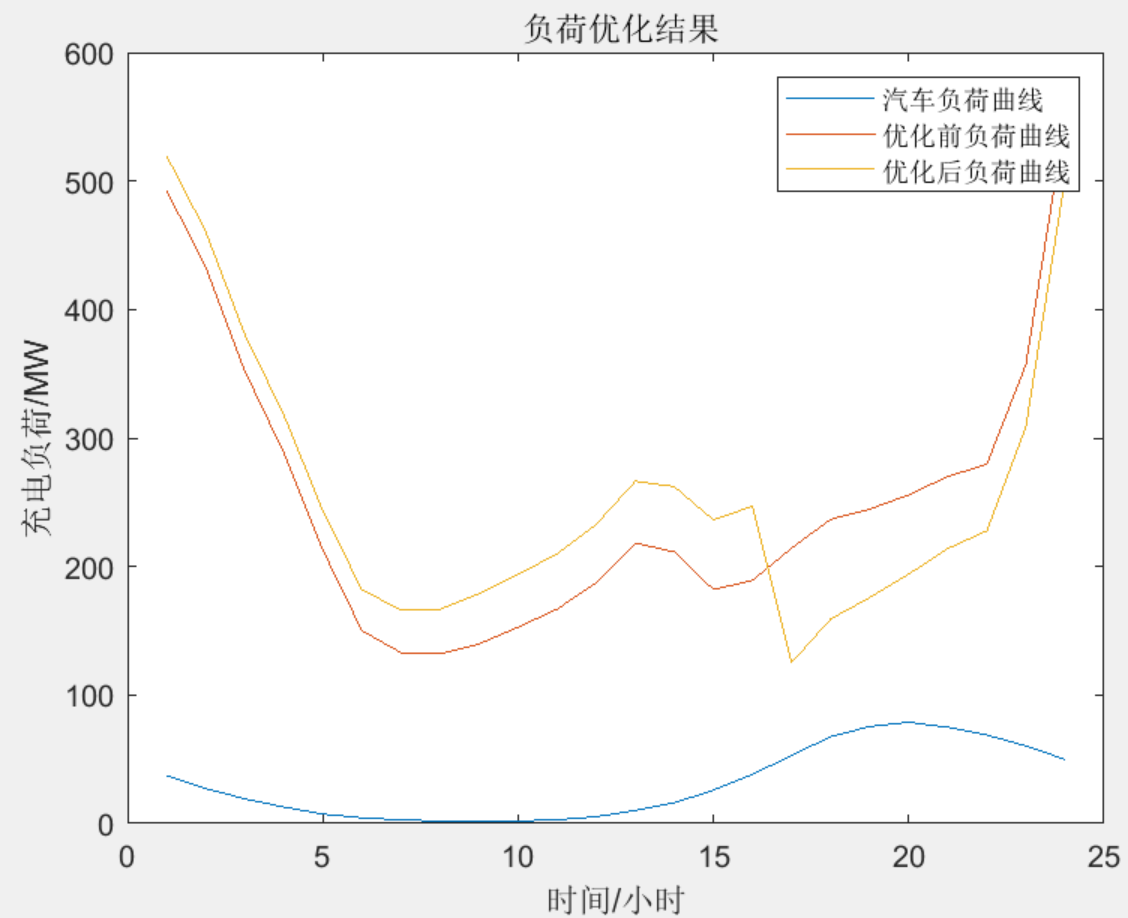
该部分利用确定好的峰谷平电价，抽取1000辆电动汽车进行分析，考虑电动汽车的充电开始时刻、充电时长、行驶路程和价格弹性矩阵，得到电动汽车充电与原始负荷对比。

2 部分代码

M=2;%目标函数个数
p=1;
pop_size=200;           % 种群规模
no_runs=1;              % 计数器
gen_max=100;            % 最大遗传代数
fname='test_case';      % 目标函数    
V=3;                    %优化变量的数量
txl=[-5*ones(1,V);zeros(1,V);-5*ones(1,V);-1000*ones(1,V);zeros(1,V);-1/sqrt(V)*ones(1,V);zeros(1,V); 0 -5*ones(1,V-1);zeros(1,V)];
txu=[10*ones(1,V); ones(1,V);5*ones(1,V);1000*ones(1,V);ones(1,V);1/sqrt(V) *ones(1,V);ones(1,V);1 5*ones(1,V-1);ones(1,V)];
xl=[0.2  0.25  0.25] ;      % 变量的下限，最低电价0.25元每千瓦时
xu=[2  2  2] ;              % 变量的上限，最高电价2元每千瓦时
etac = 20;                  % 交叉分布指数
etam = 20;                  % 突变分布指数/突变常数
pm=1/V;                     % 变异概率
pcars=caculateload(1000);   %无序时负荷
 %原电网24小时负荷
 p0=[  455.39
       405.948
       333.086
       275.836
       205.576
       145.725
       130.112
       130.112
       137.918
       150.929
       163.941
       182.156
       208.178
       195.167
       156.134
       150.929
       161.338
       169.145
       169.145
       176.952
       195.167
       210.781
       296.654
       497.026];
%价格弹性矩阵，初始电价1元
priceq=[-0.623   0.3241    0.2305;       %峰时弹性16-24
        0.3553   -0.6166   0.2216;      %平时弹性8-16
        0.3215   0.3038   -0.6065];     %谷时弹性0-8 
Q=[]; 
for run = 1:no_runs    
    %% 原始种群
    xl_temp=repmat(xl, pop_size,1);
    xu_temp=repmat(xu, pop_size,1);
    x = xl_temp+((xu_temp-xl_temp).*rand(pop_size,V));