某公司积累了21个项目缺陷个数与返工工作量的数据，如下表所示：

项目序号	缺陷修复工时	缺陷数
1	9433	1445
2	2990	405
3	634	74
4	647	138
5	4960	710
6	1370	246
7	740	66
8	1223	218
9	2766	528
10	8302	1378
11	626	78
12	611	151
13	811	105
14	2090	320
15	1440	235
16	5160	784
17	7100	1030
18	7560	1239
19	1737	321
20	6830	987
21	3250	473

对缺陷数与缺陷修复工时做回归分析分析得到如下的方程：

 

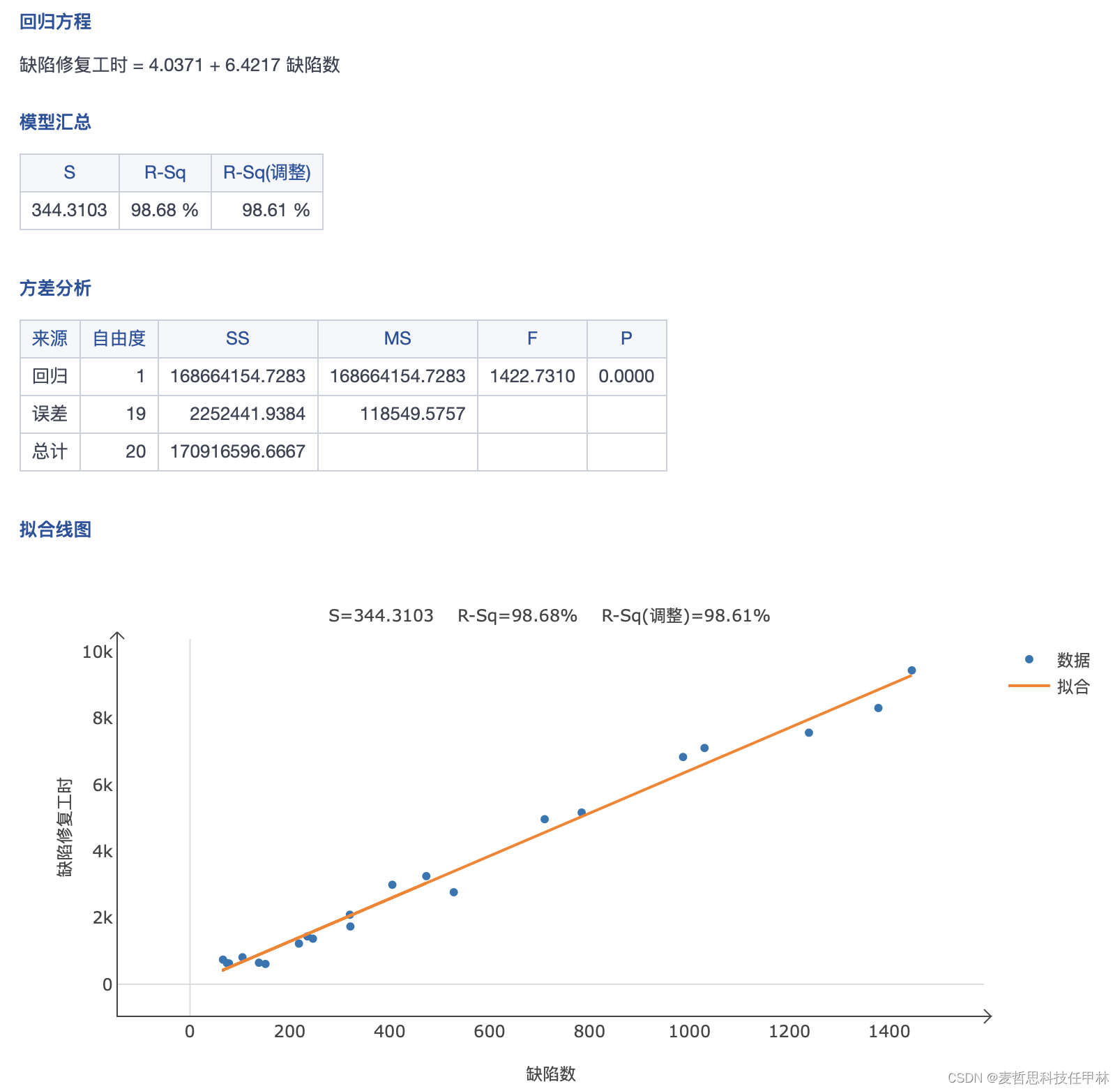
由回归方程：缺陷修复工时=4.0371+6.4217缺陷数 可以推理如下：

1 由于方程的截距为4.0371，斜率为6.4217，则修复缺陷的固定成本为4.0371个工时，每增加一个缺陷增加6.4217个工时的变动成本。

2 如果要降低返工成本，有两种方法：

1）少犯错，即x越小，y就越小。

2）提高缺陷修复的效率，降低方程中的斜率，即可以将变动成本从6.4217降至更低的数值。