1:本题暴力做法简单,重点在于我们如何剪枝:
:《曼哈顿距离》我们每走一个点就判断,当前点到终点的最短步数是不是小于当前剩余的步数,
如果大于就肯定不符合直接return,或者当步数为0时,当还没到达终点,那也return不符合
2:另外当我们到达终点时,步数要刚好用才行.
3ACcode:
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e2+10;
int n,m,t,sx,sy,ex,ey,cnt;
int idx[]={0,0,1,-1},idy[]={1,-1,0,0};
char mp[N][N];
bool vis[N][N];
void dfs(int x,int y,int left_t){
if(x==ex&&y==ey&&left_t==0){//结束
cnt++;
return;
}
//剪枝
if((abs(ex-x)+abs(ey-y))>left_t) return;//曼哈顿离终点最短距离
if(left_t==0) return;
//通过当前标记点不能到达终点,后面再通过其他路径经过这点也肯定到不了终点
//所以不用回溯
for(int i=0;i<4;i++){
int xx=x+idx[i];
int yy=y+idy[i];
if(xx<1||xx>n||yy<1||yy>m||mp[xx][yy]=='*')
continue;
dfs(xx,yy,left_t-1);
}
}
void solve() {
cin>>n>>m>>t;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>mp[i][j];
cin>>sx>>sy>>ex>>ey;
dfs(sx,sy,t);
cout<<cnt<<"\n";
}
signed main() {
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
solve();
return 0;
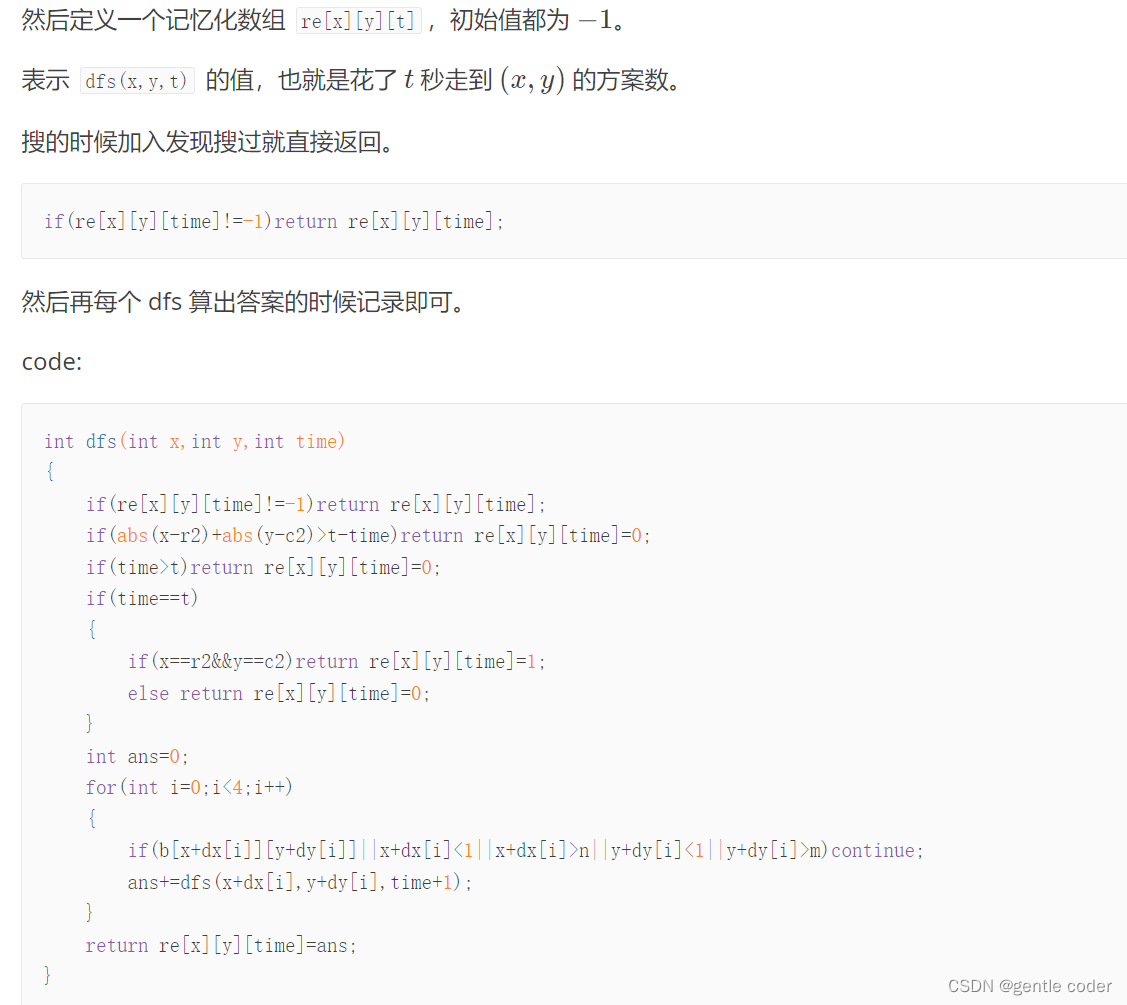
}记忆化搜索
over~