文章目录
- 一【题目类别】
- 二【题目难度】
- 三【题目编号】
- 四【题目描述】
- 五【题目示例】
- 六【题目提示】
- 七【解题思路】
- 八【时间频度】
- 九【代码实现】
- 十【提交结果】
一【题目类别】
- 栈
二【题目难度】
- 困难
三【题目编号】
- 84.柱状图中最大的矩形
四【题目描述】
- 给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
- 求在该柱状图中,能够勾勒出来的矩形的最大面积。
五【题目示例】
-
示例 1:
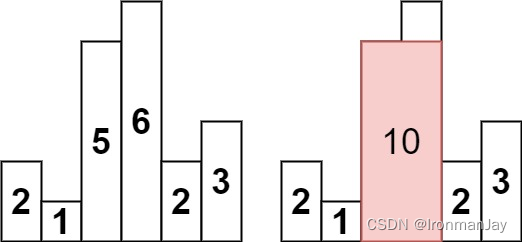
- 输入:heights = [2,1,5,6,2,3]
- 输出:10
- 解释:最大的矩形为图中红色区域,面积为 10
-
示例 2:
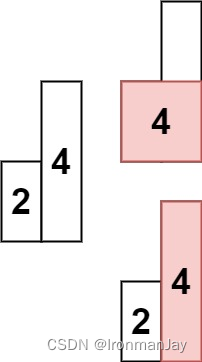
- 输入: heights = [2,4]
- 输出: 4
六【题目提示】
- 1 < = h e i g h t s . l e n g t h < = 1 0 5 1 <= heights.length <=10^5 1<=heights.length<=105
- 0 < = h e i g h t s [ i ] < = 1 0 4 0 <= heights[i] <= 10^4 0<=heights[i]<=104
七【解题思路】
- 利用单调栈的思想,这个单调栈是递增的单调栈
- 对于某一个柱子能组成的最大矩形,我们的目的是找到左边和右边的第一个小于此柱子高度的柱子(短板效应)
- 所以我们从左向右遍历数组,如果当前柱子的高度大于或等于栈顶柱子的高度,那么就入栈,因为我们维护的是单调递增的单调栈,所以对于当前柱子来说,它的左边界就是当前的栈顶元素;如果当前柱子的高度小于栈顶柱子的高度,说明找到了右边界,当前柱子就是栈顶柱子的右边界
- 当我们找到左右边界后,作差就是矩形的底,然后乘以当前柱子的高,就是当前柱子可以组成的最大矩形
- 遍历数组比较求出最大矩形值
- 最后返回结果即可
八【时间频度】
- 时间复杂度: O ( n ) O(n) O(n), n n n为传入数组的长度
- 空间复杂度: O ( n ) O(n) O(n), n n n为传入数组的长度
九【代码实现】
- Java语言版
class Solution {
public int largestRectangleArea(int[] heights) {
int[] temp = new int[heights.length + 2];
System.arraycopy(heights,0,temp,1,heights.length);
Deque<Integer> stack = new LinkedList<Integer>();
int res = 0;
for(int i = 0;i<temp.length;i++){
while(!stack.isEmpty() && temp[i] < temp[stack.peek()]){
int h = temp[stack.pop()];
int right = i;
int left = stack.peek();
int w = right - left - 1;
res = Math.max(res,w * h);
}
stack.push(i);
}
return res;
}
}
- C语言版
int largestRectangleArea(int* heights, int heightsSize)
{
int* temp = (int*)calloc(heightsSize + 2,sizeof(int));
for(int i = 1;i <= heightsSize;i++)
{
temp[i] = heights[i - 1];
}
int* stack = (int*)calloc(heightsSize + 2,sizeof(int));
int top = -1;
int res = 0;
for(int i = 0;i < heightsSize + 2;i++)
{
while(top != -1 && temp[i] < temp[stack[top]])
{
int h = temp[stack[top--]];
int right = i;
int left = stack[top];
int w = right - left - 1;
res = fmax(res,w * h);
}
stack[++top] = i;
}
return res;
}
- Python语言版
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
heights.append(0)
heights.insert(0,0)
stack = []
res = 0
for i in range(0,len(heights)):
while len(stack) != 0 and heights[i] < heights[stack[-1]]:
h = heights[stack.pop()]
right = i
left = stack[-1]
w = right - left - 1
res = max(res,w * h)
stack.append(i)
return res
- C++语言版
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
heights.insert(heights.begin(),0);
heights.push_back(0);
stack<int> st;
int res = 0;
for(int i = 0;i<heights.size();i++){
while(!st.empty() && heights[i] < heights[st.top()]){
int h = heights[st.top()];
st.pop();
int right = i;
int left = st.top();
int w = right - left - 1;
res = fmax(res,w * h);
}
st.push(i);
}
return res;
}
};
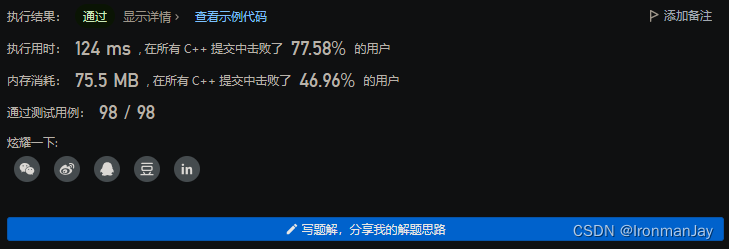
十【提交结果】
-
Java语言版
-
C语言版
-
Python语言版
-
C++语言版