早点关注我,精彩不错过!
欢迎回到数学魔术系列!久违了!
在牌序领域,一个特别数学化也是很冷门的一个序,DeBruijin序列,算是经典中的经典了。但它在魔术圈里流传并不甚广的原因是,可扩展性不强,学习记忆相对也困难,即魔术表演价值的性价比不是很高。但是作为一一对应函数,通信编码的经典结构,其数学价值仍然很高,魔术价值也可以继续挖掘。作为数学魔术师,我们还是应当奉为圭臬,好好品读,学习一番。
De Bruijin序列的数学原理
先看定义。
De Bruijn(Dutch) Sequence:DB(k) is a binary looped sequence of length 2 ^ k such that every k consecutive digits appears exactly once.
Corresponding De Bruijn Graph: 2 ^ k vertices and 2 ^ (k + 1) edges.
这是De Bruijin序列的数学描述,是这么一个首尾相接长度为2 ^ k的二进制循环序列(cyclic sequence,本质上是圈),其所有的2 ^ k个长度为k的二进制子串都互不相同,恰好与所有k长的二进制子串空间形成一一映射,是荷兰人Nicolaas Govert de Bruijn在大约1946年发表的成果。
很容易想明白,这其实就是一个图上的欧拉回路(Euler Circuit)。图的顶点是所有2 ^ (k - 1)个二进制序列,任意两个序列a, b,如果满足a[1:] = b[:- 1],便有边相连,对应的图叫De Bruijin图:
图1 De Bruijin图
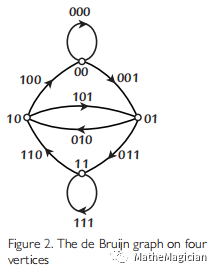
其实,根据一些对称性的规律构造,De Bruijin序列的解并不难找,而且解还有(k!) ^ (k ^ (n - 1)) / k ^ n这么多个。这里k是字母表的大小,是我们这里所说的二进制De Bruijin序列的扩展,记作D(k, n)。
正因为其良好的数学性质——一一对应,它被用在了很多应用领域。别小看了这个一一对应,不信你找一些例子,会发现这个世界上大部分的函数都没有这种性质,是不可逆的,倒不回去的。比如,你的身高是180,可是180的人却多了去了;你会变魔术,会阴魂不散,还会刘谦的版本,可满足这些条件的仍然不止你一个。不过,你要是有某个特质真的独一无二能够倒回去了,那就真厉害了。
提两个应用领域,一个是机器人定位。在机器人的运动规划中,要确定实时位置,如果是一维运动,那只需要去查其坐在位置的debruijin序列值,并唯一地对应回其真实坐标即可,就没必要一直保存其距离原点的距离,并每走一步都重新计算了。如果是二维运动,那也会有类似二维的deburijin序列,用一个n阶bool方阵和二维坐标之间的对应关系去索引位置,三维运动也是一样,只不过计算上会越来越复杂。还有一个是在寄存器上需要对一些信息进行加密的话,常用的有线性移位寄存器(linear-shift register),这样每次只需要移动一个位,就可以完成操作,而不需要每次都要移动全部数值,而这也是我们这个数学魔术的基本原理。
De Bruijin序列魔术应用方法
以上是De Bruijin序列数学内容和在各个领域中的应用信息。我们接着可以用魔术思维来尝试应用它。不妨我们来总结一下De Bruijin序列的数学本质,再看看哪些性质可以为魔术所用,自然就可以结合起来倒推出魔术应用思路了。
De Bruijin序列的本质是一个长度为k ^ n的圈,每个元素编码为k分类变量,其上刚好有k ^ n个长度为n的子序列,而且这些子序列两两不相同,构成一个序列起始位置到序列值的大小为k ^ n的一一映射。
很自然地,我们的扑克牌叠如果把底牌和顶牌的关系等效为和其他任意两张物理相邻扑克牌相同的一种关系,那也是一个圈,或者叫循环序列,对二切牌操作有对称不变性。那么k即为一张扑克牌的花色点数等基本信息可以编码出的一个信息的总数,如果限定在花色点数上,那最多54,而显然k不可能太大,常用的可以是颜色的2,花色的4,和点数的13。而假设我们构造出了这么一个De Bruijin序列性质的扑克牌,比如可以用花色编码4类信息,取n = 2,长度是16,能有什么用呢?
根据De Bruijin序列的定义,我们可以任意二切牌,不改变牌叠性质。然后任意选择相邻两张牌的子序列,只需要知道其花色的序列值,本来的起始位置到序列值的映射,因为是一一映射,就可以由观察的序列值反推到起始位置。进而所选两张牌的位置就都知道了。而在恒定不变的扑克牌序列中,位置知道了,值也就是固定的。
所以,如果我们有了满足De Bruijin序列性质的扑克牌叠,我们可以二切牌不打破它,同时我们只需要暗中通信到每张牌的k类信息值,就可以确定出选牌位置,进而读取其值。这些是整个De Bruijin序列魔术应用的全部原理,顶层本质上说,它是一一映射性质的绝妙应用,往下是进制编码,再往下是De Bruijin序列这个序列,以及旁的循环群的扑克牌叠的结构。
于是,要设计出基于De Bruijin序列的一一映射原理的魔术,还剩下的问题是:
1. 我们怎么去找到一个适合用扑克牌上的信息编码的k类编码和对应k值,在信息限度内,且方便记忆;
2. 合适大小的n,一起使得k ^ n能接近一副扑克牌的大小或其他可拓展大小;
3. 对应的De Bruijin序列D(k, n)的搜索;
4. 长度为n的子序列值到扑克牌值的方便记忆的映射(无需再记忆相对位置,因为对于一副以内的扑克牌,位置索引和牌值也是一一对应的);
5. De Bruijin序列本身的二阶递推关系,方便记忆和使用,同时展现在扑克牌上不能有明显规律;
看来问题还挺多的,不过数学魔术师不怕麻烦,只为了心中的灯塔。
k个类型怎么映射其实很明显了,算一下n次方的数量级也很容易确定合理的n;而其实你如果有一定的数感就知道,对于给定的k和n,找到一个可行的De Bruijin序列并不难,这里关键是怎么去构建一个De Bruijin序列,还能够有方便的递推公式同时子序列编码值映射回扑克牌的映射也要有一定规律能记忆才行。所以,设计出可行魔术的关键就在于序列递推关系的设计和子序列值到牌点的编码映射表。
这些东西,深深地吸引着数学魔术师们,朝着内心的求索,奔去。
下一篇我们进入魔术部分,先睹为快!
视频1 Debruijin魔术

我们是谁:
MatheMagician,中文“数学魔术师”,原指用数学设计魔术的魔术师和数学家。既取其用数学来变魔术的本义,也取像魔术一样玩数学的意思。文章内容涵盖互联网,计算机,统计,算法,NLP等前沿的数学及应用领域;也包括魔术思想,流程鉴赏等魔术内容;以及结合二者的数学魔术分享,还有一些思辨性的谈天说地的随笔。希望你能和我一起,既能感性思考又保持理性思维,享受人生乐趣。欢迎扫码关注和在文末或公众号留言与我交流!


扫描二维码
关注更多精彩
这到底是怎么想到的!!!
一道北大强基题背后的故事(七)——特征根公式的来龙去脉
用排列组合来编码通信(七)——《我的5/4张牌的预言》
好魔术背后的秘密
对称思维的妙用之从解题到本质(六)——网红鸭子半圆概率问题的多种解法

点击阅读原文,往期精彩不错过!