SVM简单理解

在下二维平面存在以下数据点，不同颜色代表不同类别，现在需要画一条直线，想将两个类别分别开来，当有新数据加入时，根据这条直线，也能将新数据正确分类，那么怎么才能画出这条线呢？对于下面这几种不同的画法，你会怎么选择。那么在三维空间、四维空间、高维空间，你又该怎样确定超平面划分两类数据呢？
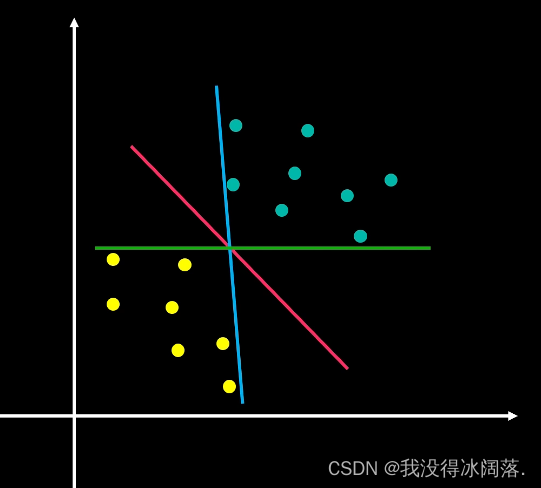
在这里插入图片描述
上面的这些问题都可以理解为，在N维数据的样本数，M维数据的维度数，设计一个维度为M-1的超平面 $W_{1}X_{1}+ W_{2}X_{2}+ ……+ W_{m}X_{m}+B = 0$ 将两类数据区别开来，W可以理解为X对应的权重

下面以二维空间为例，找到那条分类线W_{1}X_{1}+ W_{2}X_{2}+B = 0 作为决策边界。下面看一下几种不同的画法，看看那一条边界能够很好分类数据。
第一种画法中，两类数据都有数据点离边界非常接近，这种画法效果是非常差的，当有一个点同样接近分类线时，分类错误的概率是非常大的。
第二种画法中，两类数据中所有点，都与决策边界线保持一定的距离，这个距离起到缓冲区的作用，当这个缓冲区足够大时，分类结果的可信度就更高了，我们把这个缓冲区称为间隔。间隔能够把两类数据所处的空间分割开来，间隔距离可以体现分类数据差异的大小，越大的间隔，意味着两类数据差异越大，我们区分起来就越容易。因此，寻找最佳决策边界线的问题，可以转化为求解两类数据的最大间隔问题。间隔的中间，就是我们的决策边界。
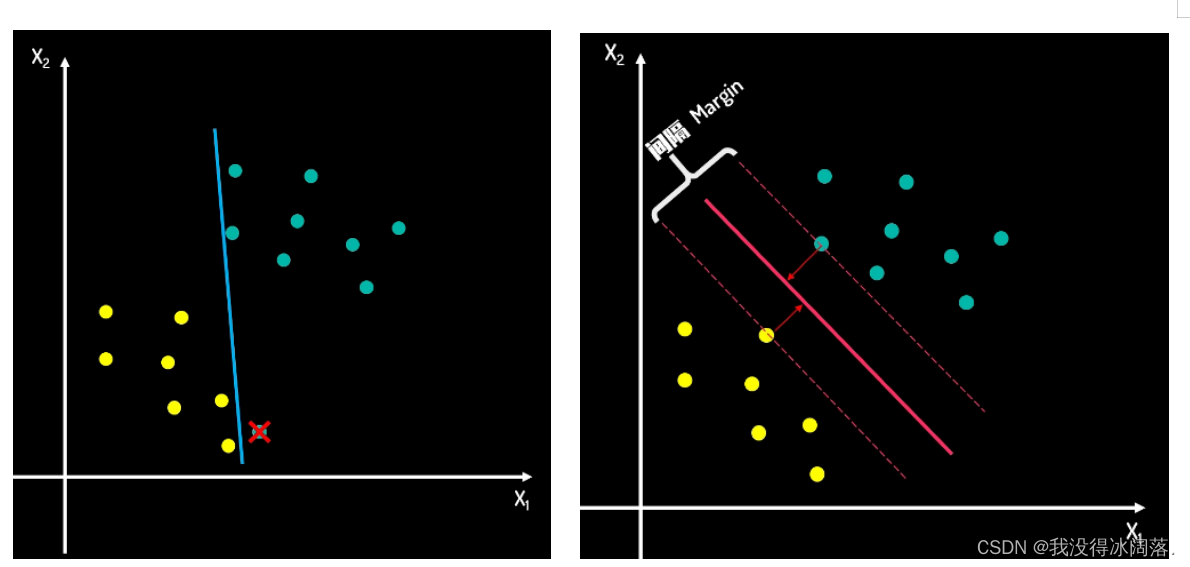
在这里插入图片描述
当有新数据需要判断时，根据它处于决策边界的相对位置，就可以进行分类了。假设决策边界的超平面方程式为W_{1}X_{1}+ W_{2}X_{2}+B = 0 它分别上下移动c，来到间隔上下边界W_{1}X_{1}+ W_{2}X_{2}+B = c 和W_{1}X_{1}+ W_{2}X_{2}+B = -c ，上下边界一定会经过一些样本边界的点，这些点距离决策边界最近，他们决定了间隔边界距离，我们称他们为支持向量（support vector），我们的支持向量机就是support vector machine，简称SVM。
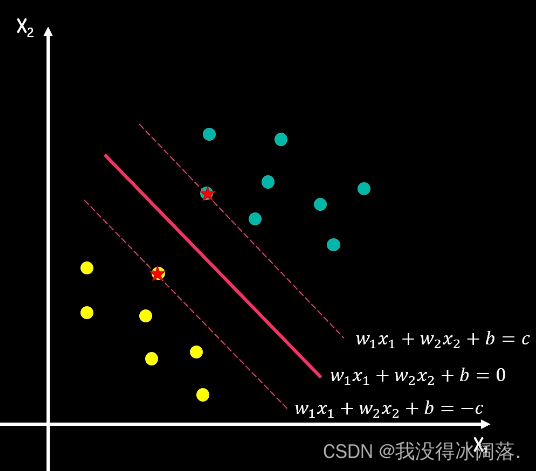
在这里插入图片描述
我们把等式两边分别除以c，得到
$W_{1}X_{1}+ W_{2}X_{2}+B = 0 ->\frac{W1}{c} _{}X_{1}+ \frac{W2}{c} X_{2}+\frac{b}{c} = 0$
$W_{1}X_{1}+ W_{2}X_{2}+B = 0 ->\frac{W1}{c} _{}X_{1}+ \frac{W2}{c} X_{2}+\frac{b}{c} = 1$
$W_{1}X_{1}+ W_{2}X_{2}+B = 0 ->\frac{W1}{c} _{}X_{1}+ \frac{W2}{c} X_{2}+\frac{b}{c} = 1$
$W_{1}^{'}=\frac{W_{1}}{c} ， W_{2}^{'}=\frac{W_{2}}{c}，b_{}^{'}=\frac{b_{}}{c}$
使用 $W_{1}^{'}$ , $W_{2}^{'}$ , $b_{}^{'}$ 分别替代原方程的变量，得到新方程：
$w_{1}{'}x_{1}+ w_{2}{'}x_{2}+b_{}{'} = 0$
$w_{1}{'}x_{1}+ w_{2}{'}x_{2}+b_{}{'} = 1$
$w_{1}{'}x_{1}+ w_{2}{'}x_{2}+b_{}{'} = -1$
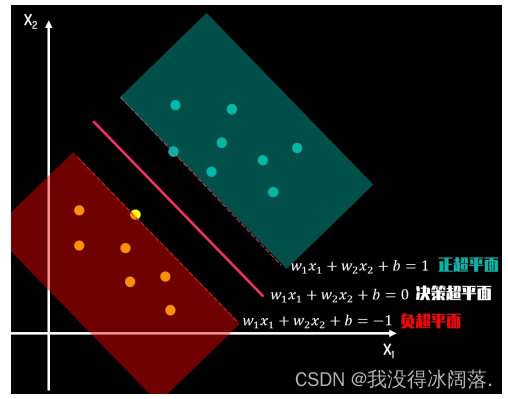
方程右边被转化为正负一，这样我们就可以将上述两个方程式定义为正负超平面，只需要求解 $W_{}{'}$ , $b_{}{'}$ ，得到对应的三个超平面方程式。正超平面及其上面的点成为正类，负超平面以及下面的点成为负类。当有新数据加入，需要判断时，只需要判断他与决策超平面的绝对位置进行分类。
在这里插入图片描述

SVM代码实现

导入数据集

对文件进行逐行解析，从而得到第行的类标签labelMat和整个特征矩阵dataMat。
下一个函数selectJrand ()有两个参数值,其中i是第一个alpha的下标,m是所有alpha的数目。只要函数值不等于输入值i,函数就会进行随机选择。clipAlpha ()它是用于调整大于H或小于L的alpha值。
在这里插入图片描述

def loadDataSet(fileName):
    dataMat = []
    labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]), float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat, labelMat
    
def selectJrand(i, m):
    j = i
    while j == i:
        j = int(random.uniform(0, m))
    return j


def clipAlpha(aj, H, L):
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj

SVM实现

Args:
    dataMatIn    数据集
    classLabels  类别标签
    C   松弛变量(常量值)，允许有些数据点可以处于分隔面的错误一侧。
        控制最大化间隔和保证大部分的函数间隔小于1.0这两个目标的权重。
        可以通过调节该参数达到不同的结果。
    toler   容错率（是指在某个体系中能减小一些因素或选择对某个系统产生不稳定的概率。）
    maxIter 退出前最大的循环次数

def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
    dataMatrix = mat(dataMatIn)
    # 矩阵转置 和 .T 一样的功能
    labelMat = mat(classLabels).transpose()
    m, n = shape(dataMatrix)

    # 初始化 b和alphas(alpha有点类似权重值。)
    b = 0
    alphas = mat(zeros((m, 1)))

    # 没有任何alpha改变的情况下遍历数据的次数
    iter = 0
    while (iter < maxIter):
        # w = calcWs(alphas, dataMatIn, classLabels)
        # print("w:", w)

        # 记录alpha是否已经进行优化，每次循环时设为0，然后再对整个集合顺序遍历
        alphaPairsChanged = 0
        for i in range(m):
            # print('alphas=', alphas)
            # print('labelMat=', labelMat)
            # print('multiply(alphas, labelMat)=', multiply(alphas, labelMat))
            # 我们预测的类别 y = w^Tx[i]+b; 其中因为 w = Σ(1~n) a[n]*lable[n]*x[n]
            fXi = float(multiply(alphas, labelMat).T*(dataMatrix*dataMatrix[i, :].T)) + b
            # 预测结果与真实结果比对，计算误差Ei
            Ei = fXi - float(labelMat[i])

            # 约束条件 (KKT条件是解决最优化问题的时用到的一种方法。我们这里提到的最优化问题通常是指对于给定的某一函数，求其在指定作用域上的全局最小值)
            # 0<=alphas[i]<=C，但由于0和C是边界值，我们无法进行优化，因为需要增加一个alphas和降低一个alphas。
            # 表示发生错误的概率: labelMat[i]*Ei 如果超出了 toler， 才需要优化。至于正负号，我们考虑绝对值就对了。
            '''
            # 检验训练样本(xi, yi)是否满足KKT条件
            yi*f(i) >= 1 and alpha = 0 (outside the boundary)
            yi*f(i) == 1 and 0<alpha< C (on the boundary)
            yi*f(i) <= 1 and alpha = C (between the boundary)
            '''
            if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):

                # 如果满足优化的条件，我们就随机选取非i的一个点，进行优化比较
                j = selectJrand(i, m)
                # 预测j的结果
                fXj = float(multiply(alphas, labelMat).T*(dataMatrix*dataMatrix[j, :].T)) + b
                Ej = fXj - float(labelMat[j])
                alphaIold = alphas[i].copy()
                alphaJold = alphas[j].copy()

                # L和H用于将alphas[j]调整到0-C之间。如果L==H，就不做任何改变，直接执行continue语句
                # labelMat[i] != labelMat[j] 表示异侧，就相减，否则是同侧，就相加。
                if (labelMat[i] != labelMat[j]):
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                # 如果相同，就没发优化了
                if L == H:
                    print("L==H")
                    continue

                eta = 2.0 * dataMatrix[i, :]*dataMatrix[j, :].T - dataMatrix[i, :]*dataMatrix[i, :].T - dataMatrix[j, :]*dataMatrix[j, :].T
                if eta >= 0:
                    print("eta>=0")
                    continue

                # 计算出一个新的alphas[j]值
                alphas[j] -= labelMat[j]*(Ei - Ej)/eta
                # 并使用辅助函数，以及L和H对其进行调整
                alphas[j] = clipAlpha(alphas[j], H, L)
                # 检查alpha[j]是否只是轻微的改变，如果是的话，就退出for循环。
                if (abs(alphas[j] - alphaJold) < 0.00001):
                    print("j not moving enough")
                    continue
                # 然后alphas[i]和alphas[j]同样进行改变，虽然改变的大小一样，但是改变的方向正好相反
                alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])
                # 在对alpha[i], alpha[j] 进行优化之后，给这两个alpha值设置一个常数b。
                # w= Σ[1~n] ai*yi*xi => b = yj- Σ[1~n] ai*yi(xi*xj)
                # 所以:   b1 - b = (y1-y) - Σ[1~n] yi*(a1-a)*(xi*x1)
                b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i, :]*dataMatrix[i, :].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i, :]*dataMatrix[j, :].T
                b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i, :]*dataMatrix[j, :].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j, :]*dataMatrix[j, :].T
                if (0 < alphas[i]) and (C > alphas[i]):
                    b = b1
                elif (0 < alphas[j]) and (C > alphas[j]):
                    b = b2
                else:
                    b = (b1 + b2)/2.0
                alphaPairsChanged += 1
                print("iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
        # 在for循环外，检查alpha值是否做了更新，如果在更新则将iter设为0后继续运行程序
        # 知道更新完毕后，iter次循环无变化，才推出循环。
        if (alphaPairsChanged == 0):
            iter += 1
        else:
            iter = 0
        print("iteration number: %d" % iter)
    return b, alphas

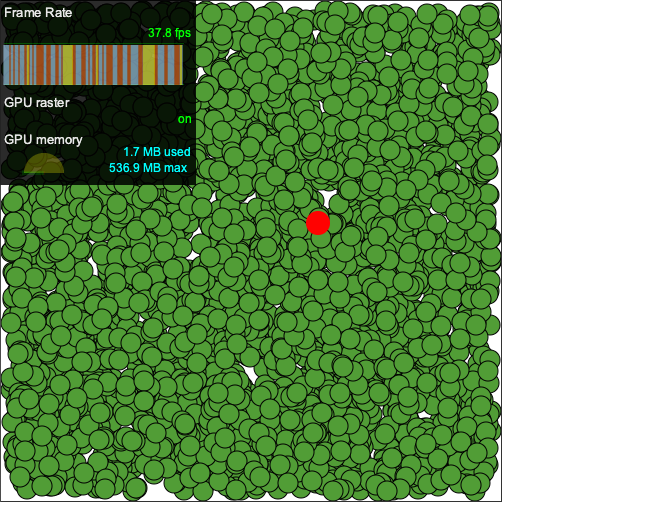
画出支持向量

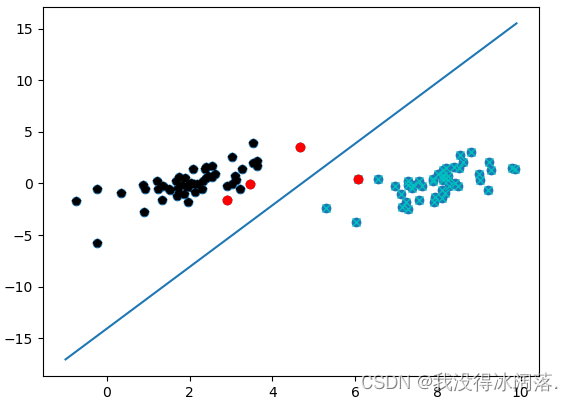
在这里插入图片描述

def plotfig_SVM(xMat, yMat, ws, b, alphas):

    xMat = mat(xMat)
    yMat = mat(yMat)

    # b原来是矩阵，先转为数组类型后其数组大小为（1,1），所以后面加[0]，变为(1,)
    b = array(b)[0]
    fig = plt.figure()
    ax = fig.add_subplot(111)

    # 注意flatten的用法
    ax.scatter(xMat[:, 0].flatten().A[0], xMat[:, 1].flatten().A[0])

    # x最大值，最小值根据原数据集dataArr[:, 0]的大小而定
    x = arange(-1.0, 10.0, 0.1)

    # 根据x.w + b = 0 得到，其式子展开为w0.x1 + w1.x2 + b = 0, x2就是y值
    y = (-b-ws[0, 0]*x)/ws[1, 0]
    ax.plot(x, y)

    for i in range(shape(yMat[0, :])[1]):
        if yMat[0, i] > 0:
            ax.plot(xMat[i, 0], xMat[i, 1], 'cx')
        else:
            ax.plot(xMat[i, 0], xMat[i, 1], 'kp')

    # 找到支持向量，并在图中标红
    for i in range(100):
        if alphas[i] > 0.0:
            ax.plot(xMat[i, 0], xMat[i, 1], 'ro')
    plt.show()

总结

优点：
1.支持向量机算法可以解决小样本情况下的机器学习问题，简化了通常的分类和回归等问题。
2.支持向量机算法利用松弛变量可以允许一些点到分类平面的距离不满足原先要求，从而避免这些
点对模型学习的影响。
——————————————————————————————————————————————————————————————————————————————————
缺点：
1.支持向量机算法对大规模训练样本难以实施。这是因为支持向量机算法借助二次规划求解支持
向量，这其中会涉及m阶矩阵的计算，所以矩阵阶数很大时将耗费大量的机器内存和运算时间。
2.经典的支持向量机算法只给出了二分类的算法一般要解决多分类问题，但支持向量机对于多分
类问题解决效果并不理想。