首先分享一段计算叶子节点数目的代码,如下图:
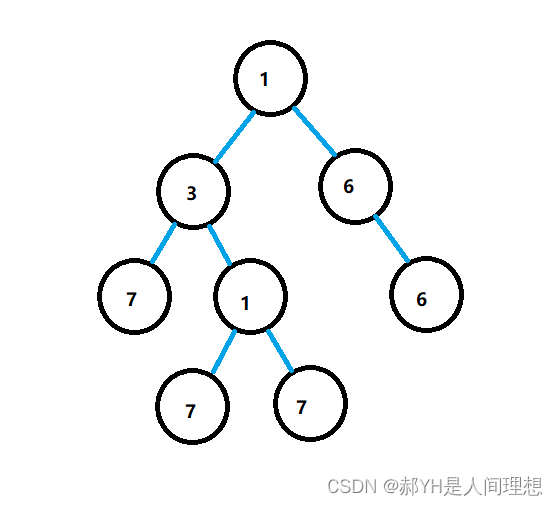
不难发现,上面的二叉树叶子节点数目为4。我们可以采用递归的方式,每当一个结点既没有左结点又没有右节点时,即可算为一个叶子结点。
int num=0;
//全局变量,代表叶子节点数
void CaculateLeafNum(BinaryNode* root)
{
if(root==NULL)
return;
if(root->lchild==NULL&&root->rchild==NULL)
num++;
//递归计算两个子树的叶子节点
CaculateLeafNum(root->lchild);
CaculateLeafNum(root->rchild);
return;
}
如上时单独的方法名,在文末的全段代码中加入即可计算,输出的 num即为叶子结点数。
众所周知,根据某一顺序单一的遍历结果,并不能唯一地确定一颗二叉树,而通过中序和先序,或者中序和后序,即可以确定唯一的一颗二叉树,但是先序和后序不能 !这是因为,通过先序或者后序,可以判断出根结点,再根据中序区分左右子树——而先序+后序就不能判断出来。
也就是说,如果已知根结点的左右子树结点数目,那么只需要知道根结点,即可判断出唯一的二叉树。这里给出一种崭新的方式,当遍历位置上的结点为空时,我们可以人为地加入结点“#”来代替空结点,这样当我们得到一种无论什么方式的遍历,都可以得出唯一地二叉树!
BinaryNode* CreateBinaryTree(){
fflush(stdin);
//清除缓存区的函数
char ch;
//标准输入
scanf("%c",&ch);
BinaryNode* node;
if(ch=='#')
node=NULL;
//用#号标识空结点
else{
node=(BinaryNode*)malloc(sizeof(BinaryNode));
//开辟内存区
node->ch=ch;
//为当前结点赋值
node->lchild=CreateBinaryTree();
//先递归创建左子树
node->rchild=CreateBinaryTree();
//再递归创建右子树
}
return node;
} 上述代码为#号法创建二叉树的具体实现。
如下是完整代码:
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
using namespace std;
typedef struct BinaryNode{
char ch;
struct BinaryNode* lchild;
struct BinaryNode* rchild;
}BinaryNode;
BinaryNode* CreateBinaryTree(){
fflush(stdin);
//清除缓存区的函数
char ch;
//标准输入
scanf("%c",&ch);
BinaryNode* node;
if(ch=='#')
node=NULL;
//用#号标识空结点
else{
node=(BinaryNode*)malloc(sizeof(BinaryNode));
//开辟内存区
node->ch=ch;
//为当前结点赋值
node->lchild=CreateBinaryTree();
//先递归创建左子树
node->rchild=CreateBinaryTree();
//再递归创建右子树
}
return node;
}
void RecursionMiddle(BinaryNode* root)
{
if(root==NULL)
return;
RecursionMiddle(root->lchild);
cout<<(root->ch)<<" ";
RecursionMiddle(root->rchild);
//中序遍历的顺序为:左-根-右
}
int main(int argc, char** argv) {
BinaryNode* root=CreateBinaryTree();
RecursionMiddle(root);
//主函数负责调用
return 0;
}先给一个简单的例子,如下是一个二叉树:
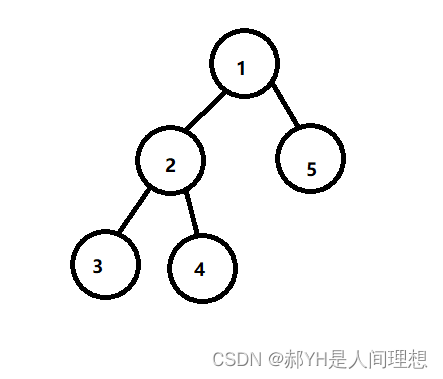
在录入结点时,先读入根结点1,然后是1的左节点2,然后是2的左节点3,由于3是叶子节点,则其左结点为#,然后是右节点,此处也为#;然后向上回溯,轮到2的右节点,此处为4,然后又轮到4的左右结点,均为#;然后是根结点1的右节点,为5,然后是5的左右结点,均为#,所以输入应该为:
1 2 3 # # 4 # # 5 # #
输入满足所有结点均有#号子节点时自动跳出递归,根据中序遍历的规则,上述的输出结果应该为:
3 2 4 1 5
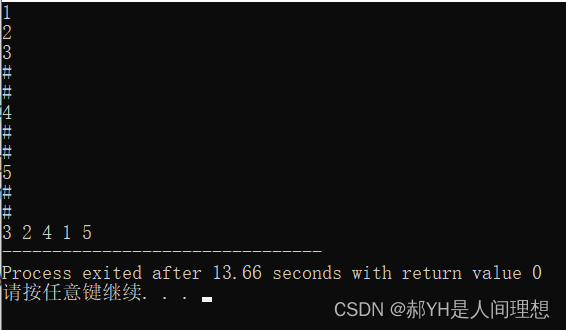
如上是运行结果,与预期保持一致!
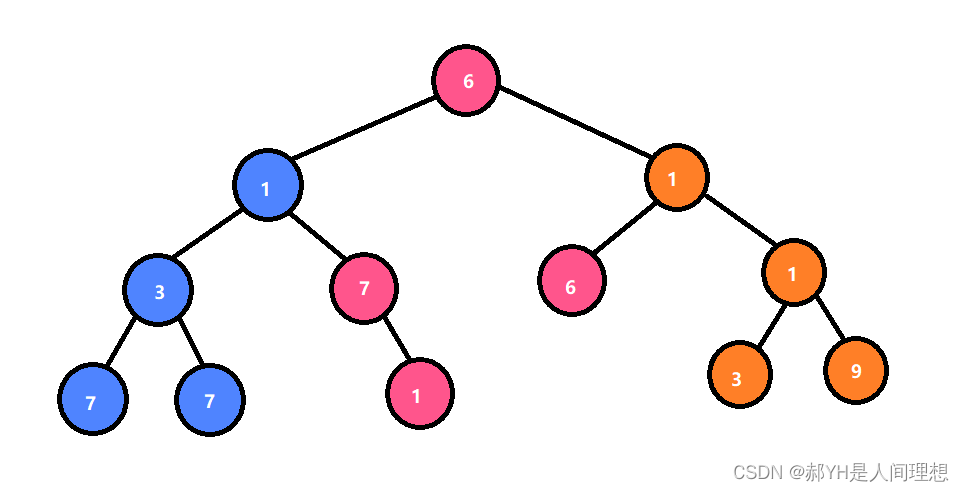
下图是一张对博主有深刻意义的二叉树图,因为这是一段藏头诗。为了防止大家在读入的时候出错,博主在此处给出读入顺序的答案:
6 1 3 7 # # 7 # 7 # 1 # # 1 6 # # 1 3 # 9 # #
运行代码并输入上述解码藏头诗的密钥,即可得出最浪漫的情话,这里就先保留悬念咯~