目录

剑指 Offer 43. 1～n 整数中 1 出现的次数

题解：

代码：

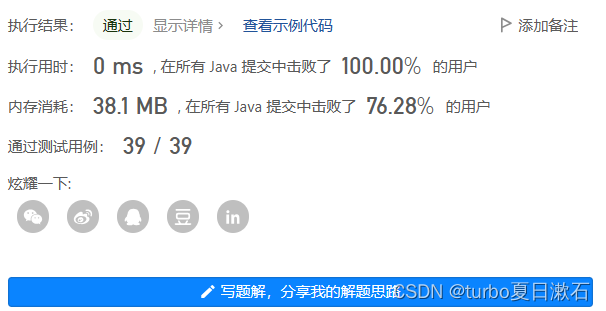
结果：

---

输入一个整数 n ，求1～n这n个整数的十进制表示中1出现的次数。

例如，输入12，1～12这些整数中包含1 的数字有1、10、11和12，1一共出现了5次。

示例 1：

输入：n = 12
输出：5
示例 2：

输入：n = 13
输出：6
 

限制：

1 <= n < 2^31

题解：

目标：找出小于等于 n 的非负整数中数字 1 出现的个数

第一瞬间想的肯定是：

①直接逐位遍历每个数的每一位，当遇到 1 的时候，计数 +1。但是会超时。

②将所有数字拼接起来，再逐位遍历。仍会超时。

废话不多说，现在来讲解更快更好的方法：

统计每一位上 1 出现的次数，个数上 1 出现的次数，十位上 1 出现的次数，百位 ，千位······

就是说小于等于 n 的所有数字中，个位上出现 1 的次数 + 十位出现 1 的次数 + ···结果就是总的出现次数。

想象自己脑子里有一个行李箱的滚轮密码锁，我们固定其中的某一位，然后可以随意滑动其他位

注：该比喻来自与网友 ryan0414，这个比喻真的很贴合本题解题思想

思路：

通过逐位计算每个位上可能出现1的次数，从个位开始向高位遍历。通过分析当前位和高低位的关系，根据不同的情况累计出现1的次数。最终得到所有位上1的总次数，并返回结果

• 初始化变量：将给定的数字n分为高位（high）、当前位（cur）和低位（low），并设置一个变量num为1来记录位数，cnt为结果计数器。

• 进入循环：通过判断当前位cur是否为0或者高位high是否为0来控制循环的进行。

• 判断当前位cur：

  • 如果当前位cur大于1，说明在该位上可能出现1的次数为(high + 1) * num。
  • 如果当前位cur等于1，说明在该位上可能出现1的次数为high * num + low + 1。其中，high * num表示高位0到high-1的数字出现的次数（cur之前的高位），low表示低位0到low的数字出现的次数。
  • 如果当前位cur等于0，说明在该位上可能出现1的次数为high * num。

• 更新变量：将num乘以10，表示进入下一位；更新cur为高位的个位数；将high除以10，舍弃掉最低位；更新low为n对num取余的结果，即低位0到low的数字。

• 循环结束后，返回结果cnt，即在给定范围内数字1出现的总次数。

代码：

class Solution {
    public int countDigitOne(int n) {
        //高位，当前位，低位
        int high=n/10;
        int cur=n%10;
        int low=0;
        //个位
        int num=1;
        //记录次数
        int cnt=0;
        //注意循环条件，有可能当前位为0时高位有数字，例如10
        while(cur!=0||high!=0){
            if(cur>1) cnt+=(high+1)*num;
            else if(cur==1) cnt+=high*num+low+1;
            else cnt+=high*num;
            num*=10;
            cur=high%10;
            high/=10;
            low=n%num;
        }
        return cnt;
    }
}

结果：