目录
摘 要:
一、 问题重述
1.1 问题背景
1.2 需要解决的问题
二、 模型假设
三、符号说明
四、问题一
4.1 问题描述与分析
4.2 模型建立
4.2.1 数据处理
4.2.2 航迹规划模型建立
4.3 求解算法建立
4.3.1 最短路径数学表达
4.3.2 自适应改进型 Dijkstra 算法求解步骤
4.3.3 自适应基于蚁群算法的飞行器航迹规划求解
4.4 模型求解及结果分析
五、问题二
5.1 问题描述与分析
5.2 模型建立
5.2.1 飞行器转弯过程分析
5.2.2 最小转弯半径约束
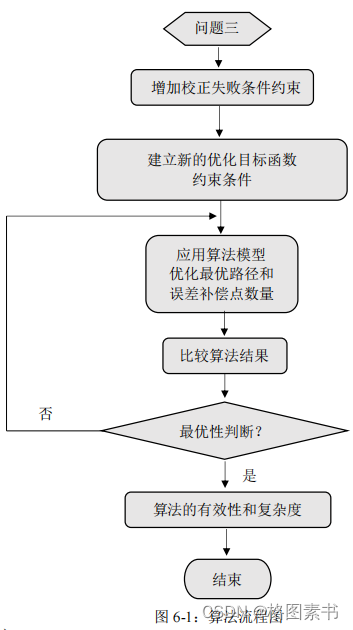
5.3 算法流程
5.4 模型求解
六、问题三
6.1 问题描述与分析
6.2 模型建立
6.2.1 误差校正情况分析
6.2.2 校正失败条件约束
6.3 模型求解
七、参考文献
代码实现
摘 要:
本文研究了多约束条件下智能飞行器航迹快速规划问题,这是一个多目标约束问题。
本文首先针对附件中的校正节点数据进行数据处理,构建从起点
A
到终点
B
的邻接距离
网络,将航迹快速规划问题转化为
0-1
多目标整数规划问题。接着通过系统建模建立
0-1
多目标整数规划模型,并通过自适应改进型
Dijkstra
算法和自适应型蚁群算法,综合求解
多目标规划模型,给出多约束条件下智能飞行器航迹快速规划的方案。
针对问题一,本文通过构架
0-1
多目标整数规划模型,以航迹长度尽可能小和经过校
正区域进行校正的次数尽可能少为目标,通过动态规划中的分阶段优化方法,给出航迹
快速规划的方案。在第一阶段利用自适应改进型
Dijkstra
算法和蚁群算法得出当前满足约
束条件的最优路径和最佳误差校正点。第二阶段,在满足约束条件的基础上,应用贪婪
算法在实际情况中对航行轨迹进一步优化。针对问题一,本文求出附件一的最优航行轨
迹为:起点
A → 503 → 69 → 237 → 155 → 338 → 457 → 555 → 436 →
终点
B
,飞行器
最短的航迹长度为
104.9 × 10
3
m
,经过校正区域进行校正的次数为
8
次;附件二的最优
航行轨迹为:起点
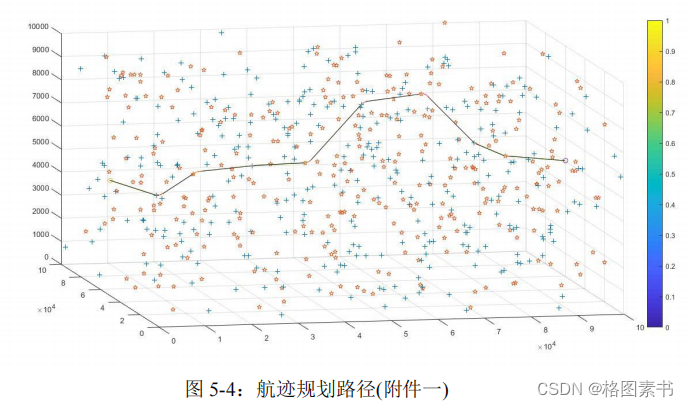
A → 163 → 114 → 8 → 309 → 305 → 123 → 45 → 160 ⟶ 92 → 93 ⟶
61 ⟶ 292 ⟶
终点
B
,飞行器最短的航迹长度为109.34 × 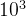 m
,经过校正区域进行校正
m
,经过校正区域进行校正
的次数为
12
次。
针对问题二,与第一问不同的是,问题二增加了飞行器在实际飞行过程中有
200
米
的最小转弯半径约束。本文通过系统分析最小转弯半径约束对飞行器实际飞行路程和能
否成功到达的影响,重新构建邻接距离网络和多目标规划模型。接着,通过问题一算法
模型与优化思路,求到附件一重新满足新约束条件的最优航行轨迹为:起点
A → 503 →
69 → 237 → 155 → 338 → 457 → 555 → 436 →
终点
B
,飞行器最短的航迹长度为
104.903 × 10
3
𝑚
,经过校正区域进行校正的次数为
8
次;附件二的最优航行轨迹为:
起点
A → 163 → 114 → 8 → 309 → 305 → 123 → 45 → 160 → 92 ⟶ 93 ⟶ 61 ⟶ 292 ⟶
终点
B
。飞行器最短的航迹长度为109.464 × 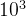 𝑚
,经过校正区域进行校正的次数为 12
𝑚
,经过校正区域进行校正的次数为 12

 时,飞行器将不再能够按照 200m的最小转弯半径调整飞行方向。在这种情况下,飞行器将按照更大的转弯半径,绕更大的弧形轨迹并中转更多的校正节点才能到达
时,飞行器将不再能够按照 200m的最小转弯半径调整飞行方向。在这种情况下,飞行器将按照更大的转弯半径,绕更大的弧形轨迹并中转更多的校正节点才能到达
 即在问题二的八个约束条件(1)~(
8
)下,飞行器
最短的
航迹长度为
104.903 ×
即在问题二的八个约束条件(1)~(
8
)下,飞行器
最短的
航迹长度为
104.903 × 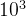 𝑚
;
𝑚
;
 该路径经过 8 个校正点,总路程为
104.903
公里。算法迭代次数为
425
次,执行时间
该路径经过 8 个校正点,总路程为
104.903
公里。算法迭代次数为
425
次,执行时间
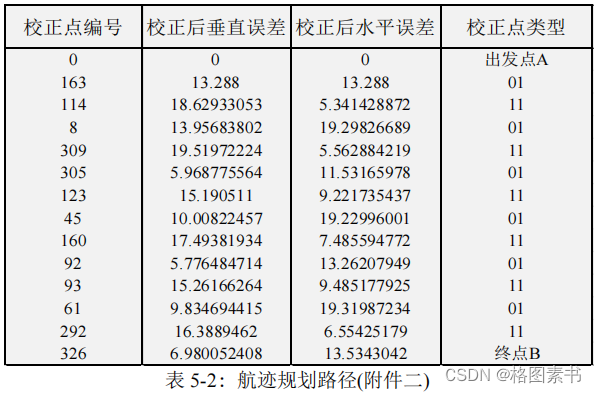
 附件二:
附件二:
 即在问题二的八个约束条件(1)
~
(
8
)下,飞行器最短的航迹长度为109.464𝑚
;经
即在问题二的八个约束条件(1)
~
(
8
)下,飞行器最短的航迹长度为109.464𝑚
;经
 该路径经过 12 个校正点,总路程为
109.464
公里。算法迭代次数为
92
次,执行时间
该路径经过 12 个校正点,总路程为
109.464
公里。算法迭代次数为
92
次,执行时间

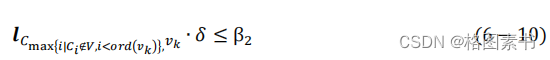 问题三的目标是在增加部分可能发生误差校正故障点的基础上,规划航行轨迹
问题三的目标是在增加部分可能发生误差校正故障点的基础上,规划航行轨迹

 正节点编号、校正前垂直误差、校正前水平误差和校正点类型如下表所示:
正节点编号、校正前垂直误差、校正前水平误差和校正点类型如下表所示:
 该路径经过 9 个校正点,总路程为
105.77
公里。算法迭代次数为
586
次,执行时间为
该路径经过 9 个校正点,总路程为
105.77
公里。算法迭代次数为
586
次,执行时间为
 即在问题三的七个约束条件(1)
~
(
7
)下,飞行器最短的航迹长度为
即在问题三的七个约束条件(1)
~
(
7
)下,飞行器最短的航迹长度为
 该路径经过 21 个校正点,总路程为
155.07
公里。算法迭代次数为
1440
次,执行时间
该路径经过 21 个校正点,总路程为
155.07
公里。算法迭代次数为
1440
次,执行时间
 因此综合上述结果来看,放松成功概率的情况下,飞行器航行轨迹长度
和经过的
节点
因此综合上述结果来看,放松成功概率的情况下,飞行器航行轨迹长度
和经过的
节点

次。
针对问题三,与问题一不同的是,在飞行器飞行的实际情况中,问题三增加了部分可
能发生误差校正失败的故障点。本文根据故障点分布和误差调整类型,重新构建邻接距离
网络和多目标规划模型,增加目标函数和约束条件。接着,应用问题一的自适应改进型
Dijkstra
算法和蚁群算法,重新规划航行轨迹。
与前两问相比,为了使飞行器成功到达的概率尽可能大,问题三在满足约束条件的基
础上,通过不断放松和改变校正节点的方法,求得附件一航行轨迹为:
起点
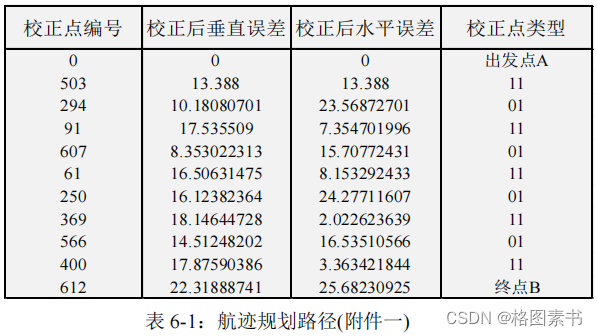
A → 503 → 294 → 91 → 607 → 61 → 250 → 369 → 566 → 400 ⟶
终点
B
,飞行器最
短的航迹长度为
105.77 × 10
3
𝑚
,经过校正区域进行校正的次数为
9
次,成功概率为
100%
;
接着综合考虑实际情况,当把针对附件二中的数据,求得成功到达概率目标约束为 100%、
最优航行路径有:起点
A → 140 → 226 → 288 → 306 → 237 → 280 → 65 → 142 → 310 ⟶
7 ⟶ 145 ⟶ 293 ⟶ 156 ⟶ 213 ⟶ 164 ⟶ 50 ⟶ 247 ⟶ 38 ⟶ 110 ⟶ 99 ⟶ 292 ⟶
终点
B
。飞行器最短的航迹长度为155.07 × 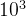 m,经过校正区域进行经过的校正节点个数
m,经过校正区域进行经过的校正节点个数
为为
21
个,成功概率为
100%
。
关键词:
邻接距离网络,自适应改进型
Dijkstra
算法,蚁群算法,
0-1
多目标整数规划,
多目标规划模型,贪婪算法,复杂网络,分阶段优化
一、 问题重述
1.1 问题背景
复杂环境下航迹快速规划是智能飞行器控制的一个重要课题。由于系统结构限制,这
类飞行器的定位系统无法对自身进行精准定位,一旦定位误差积累到一定程度可能导致任
务失败。因此,在飞行过程中对定位误差进行校正是智能飞行器航迹规划中一项重要任务。
1.2 需要解决的问题
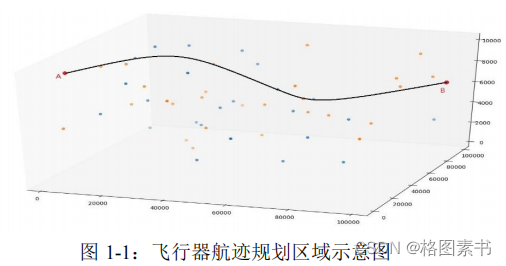
本题目是研究智能飞行器在系统定位精度限制下的航迹快速规划问题。假设飞行器的
飞行区域如图
1
所示,出发点为
A
点,目的地为
B
点。其航行需要满足的约束如下:
(1)
飞行器在空间飞行过程中需要实时定位,其定位误差包括垂直误差和水平误差。飞
行器每飞行
1m
,垂直误差和水平误差将各增加
δ
个专用单位,以下简称单位。到达
终点时垂直误差和水平误差均应小于
𝜃
个单位,并且为简化问题,假设当垂直误差
和水平误差均小于
𝜃
个单位时,飞行器仍能够按照规划路径飞行。
(2)
飞行器在飞行过程中需要对定位误差进行校正。飞行区域中存在一些安全位置(称
之为校正点)可用于误差校正,当飞行器到达校正点即能够根据该位置的误差校正
类型进行误差校正。校正垂直和水平误差的位置可根据地形在航迹规划前确定(如
图
1
为某条航迹的示意图
,
黄色的点为水平误差校正点,蓝色的点为垂直误差校正
点,出发点为
A
点,目的地为
B
点,黑色曲线代表一条航迹)。可校正的飞行区
域分布位置依赖于地形,无统一规律。若垂直误差、水平误差都能得到及时校正,
则飞行器可以按照预定航线飞行,通过若干个校正点进行误差校正后最终到达目的
地。

(3)
在出发地
A
点,飞行器的垂直和水平误差均为
0
。
(4)
飞行器在垂直误差校正点进行垂直误差校正后,其垂直误差将变为
0
,水平误差保
持不变。
(5)
飞行器在水平误差校正点进行水平误差校正后,其水平误差将变为
0
,垂直误差保
持不变。
(6)
当飞行器的垂直误差不大于
α
1
个单位,水平误差不大于
α
2
个单位时才能进行垂直误
差校正。
(7)
当飞行器的垂直误差不大于
β
1
个单位,水平误差不大于
β
2
个单位时才能进行水平误
差校正。
(8)
飞行器在转弯时受到结构和控制系统的限制,无法完成即时转弯
(
飞行器前进方向
无法突然改变
)
,假设飞行器的最小转弯半径为
200m
。
需要通过建立数学模型,为上述智能飞行器建立从
A
点飞到
B 点满足上述约束条件
的航迹规划一般模型和算法。解决以下几个问题:
问题
1.
针对附件
1
和附件
2
中的数据分别规划满足条件(
1
)
~
(
7
)时飞行器的航迹,
并且综合考虑以下优化目标:
(
A
)航迹长度尽可能小;(
B
)经过校正区域进行校正的次数尽可能少。
讨论算法的有效性和复杂度,并绘出两个数据集的航迹规划路径。
问题
2.
针对附件
1
和附件
2
中的数据(参数与第一问相同)分别规划满足条件(
1
)
~
(
8
)时飞行器的航迹,并且综合考虑以下优化目标:
(
A
)航迹长度尽可能小;(
B
)经过校正区域进行校正的次数尽可能少。
讨论算法的有效性和复杂度,并绘出两个数据集的航迹规划路径(直线用黑色,圆弧
用红色)。
问题
3.
飞行器的飞行环境可能随时间动态变化,虽然校正点在飞行前已经确定,但飞
行器在部分校正点进行误差校正时存在无法达到理想校正的情况(即将某个误差精确校正
为
0
),例如天气等不可控因素导致飞行器到达校正点也无法进行理想的误差校正。现假
设飞行器在部分校正点(附件
1
和附件
2
中
F
列标记为“
1
”的数据)能够成功将某个误差
校正为
0
的概率是
80%
,如果校正失败,则校正后的剩余误差为
min(error
,
5)
个单位(其
中
error
为校正前误差,
min
为取小函数),并且假设飞行器到达该校正点时即可知道在该
点处是否能够校正成功,但不论校正成功与否,均不能改变规划路径。针对此情况重新规
划问题
1
所要求的航迹,要求成功到达终点的概率尽可能大,并绘出两个数据集的航迹规
划路径。
二、 模型假设
为了便于问题的研究,对题目中某些条件进行简化及合理的假设。
1
、忽略无人机自身大小对路径长度的影响,将无人机视为质点;
2
、无人机总能恰好经过校正区点;
3
、无人机在飞行途中不会遇到障碍物;
4
、无人机到达一个校正区后立刻转弯飞向下一个校正区或终点;
5
、为使路径长度尽可能小
,
无人机在转弯时只以最小转弯半径进行转弯。
三、符号说明

四、问题一
4.1 问题描述与分析
问题一是研究智能飞行器在系统定位精度限制下的航迹快速规划问题。要针对附件
1
和附件
2
中的地点位置数据和地点安全类型,分别从
A
点出发到达目的地
B
点,规划满足
约束条件(
1
)
~
(
7
)时飞行器的航行轨迹,并且综合考虑以下优化目标:(
A
)航迹长度
尽可能小;(
B
)经过校正区域进行校正的次数尽可能少。讨论算法的有效性和复杂度,并
绘出两个数据集的航迹规划路径,并将结果(即飞行器从起点出发经过的误差校正点编号
及校正前误差)依次填入航迹规划结果表中。
其中附件
1
数据的参数为
:
α
1
= 25
,
α
2
= 15
,
β
1
= 20
,
β
2
= 25
,
𝜃 = 30
,
𝛿 = 0.001
附件
2
中数据的参数为:
α
1
= 20
,
α
2
= 10
,
β
1
= 15
,
β
2
= 20
,
𝜃 = 20
,
𝛿 = 0.001
问题一的目的是在使得航迹长度尽可能小的同时,经过校正区域进行校正的次数也尽
可能少,即为多目标动态规划问题。由于智能飞行器在飞行过程中每飞行
1m
,垂直误差和
水平误差将各增加
𝛿
个专用单位使得智能飞行器在飞行过程中必须选择误差校正位置进行
垂直或者水平误差调整,而不能直接选择从起点到终点的航行轨迹。智能飞行器的航迹长
度大小与飞行器在飞行过程中选择的校正点位置、校正点的垂直或水平误差校正类型有关。
经过校正区域进行校正的次数与飞行器在飞行过程中不断累加的飞行定位误差值、每个校
正点允许的垂直或水平误差阈值
α, β
个单位和终点
B
允许到达的垂直误差和水平误差
𝜃
个
单位。需要注意的是飞行器在飞行过程中需要不断调整飞行方向以达到航迹长度尽可能小
的目的。
根据题目和参考文献,给出智能飞行器轨迹规划策略如下:
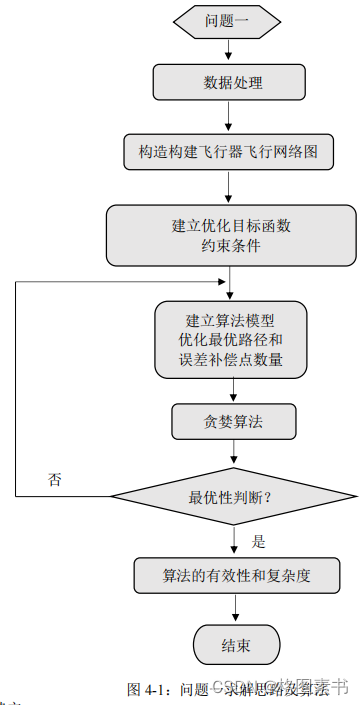
(
1
)对附件中的起点
A
、校正节点和终点
B
的三维坐标以及校正点类型进行数据处理,构
建飞行器飞行邻接距离矩阵,并在邻接距离矩阵中剔除不满足条件的校正节点关系,从而
构建飞行器飞行网络图。
(
2
)飞行器在飞行过程中需要满足飞行路程最短的同时,尽可能经过少的飞行误差校正节
点。此时我们通过建模选择最优路线和最佳误差点数量和。
(
3
)根据最优路线和最佳误差点数量和带入实际问题中综合考虑多目标规划问题的最优
解。
(
4
)以上问题中,不考虑无人机大小,无人机为质点。
(
5
)应用不同算法,应用自适应改进型
Dijkstra
算法与基于蚁群寻优的智能优化蚁群算法
在解决组合优化问题,通过调整数据,应用贪婪算法对航行轨迹进一步优化。

4.2 模型建立
4.2.1 数据处理
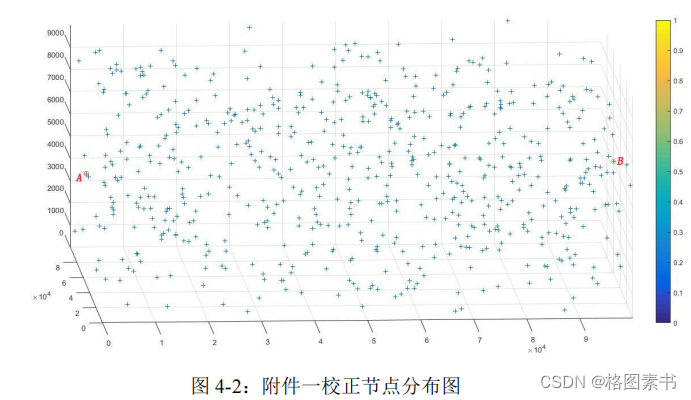
根据附件中的起点
A
、校正节点和终点
B
的三维坐标以及校正点类型,以附件一为例,
从起点
A
到终点
B
共有
611
个水平和垂直节点,如下图 4-2 所示。

首先进行数据处理,构建飞行器飞行邻接距离矩阵。邻接距离矩阵的基本原理是将图
中
n
个顶点的数据存放在一组一维数组中,用一个
n × n
矩阵的形式来表示各个顶点间的
邻接关系。图可分为有向图和无向图,在飞行器的航迹规划中,涉及到的是无向图。其中
网络图的实质是结构较为复杂的一种数据结构,图的基本信息由两个部分组成:图中所有
顶点的数据和各个顶点之间的关系,即边或者弧的关系。并在邻接距离矩阵中剔除不满足
条件的校正节点关系,从而构建飞行器飞行网络图。
设
D
’
为无向图,根据
D
’
的各个顶点之间是否可以直接连接,编写一个矩阵,
1
表示可以
直接连接,0 表示不能直接连接,其定义如下:


因为任何顶点自身不能相连,所以在任何无向图的邻接矩阵中,主对角线一定皆为
0
,
其余可以相连的顶点皆为 1。由此可得,每个无向图的邻接矩阵皆为关于主对角线对称的
n
×
n
的矩阵。邻接矩阵中包含了图的一切性质,邻接矩阵与它所唯一对应的图成一一对应
关系。
针对于本题的航迹规划问题,将无向图转化为飞行器飞行网络图
S
,也就是测量出各个
可以相连的校正点之间的距离,将无向图邻接矩阵中的“
1
”用实际距离代替
,并在邻接距
离矩阵中剔除不满足条件的校正节点关系,从而构建飞行器飞行网络图。即其中针对相连
的各个顶点之间的距离不满足最大允许调整的水平和垂直误差,用“∞”表示,即将无向
图邻接矩阵中的“0”用“∞”代替。
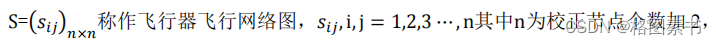
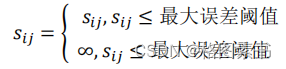
经过数据处理得到的飞行器飞行网络图如图
4-3
所示:
4.2.2 航迹规划模型建立
根据校正节点的数据处理得到的飞行器飞行网络图,飞行器在从起点 A 到终点 B 飞行
过程中需要满足飞行路程最短的同时,尽可能经过少的飞行误差校正节点。我们通过建模
选择最优路线和最佳误差点数量和,这是一个多目标动态规划问题。飞行器在飞行过程中



Step3:
直到完成所有校正节点的编号和校正节点判断。
首先根据问题一的规定模型假设:首先假设飞行器从一个校正节点到另一个校正节点
之间始终匀速直线运动,忽略转弯引起的轨迹变化。飞行器在从起点
A
到终点
B
的飞行过
程中需要依次选择水平校正节点和垂直校正节点进行误差校正,以满足能够在误差允许的
 点。我们通过建模选择最优路线和最佳误差点数量和。
点。我们通过建模选择最优路线和最佳误差点数量和。
范围内到达各个水平或者垂直校正节点进行水平和垂直误差校正。其中需要注意的是飞行
器到达终点
B
的允许误差和到达各校正节点的允许误差值是不一致的,这是一个多目标航
迹规划问题。多目标规划的优化目标是获得在从起点
A
到终点
B的飞行中,航迹路程最小的


约束条件包括:
⑴飞行器在空间飞行过程中需要实时定位,其定位误差包括垂直误差和水平误差。飞
行器每飞行
1m
,垂直误差和水平误差将各增加δ个专用单位,则飞行器从起点或者校正点



⑷飞行器在飞行过程中会根据最优路径和节点数选择经过水平误差补偿和垂直误差
补偿点,在算法的实际计算中常常需要直接约束任意两个水平或者垂直误差的阈值,约束
条件如下所示:
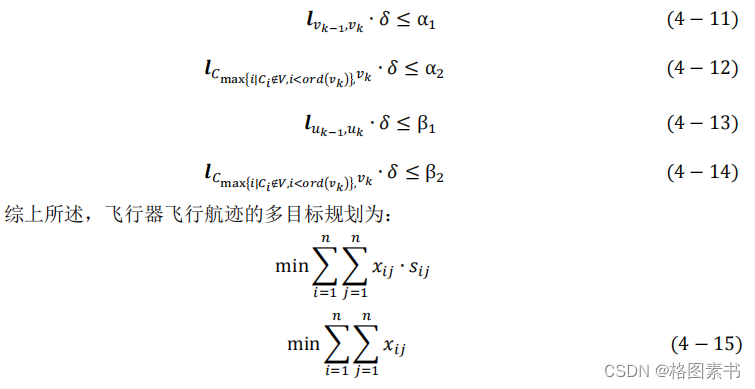
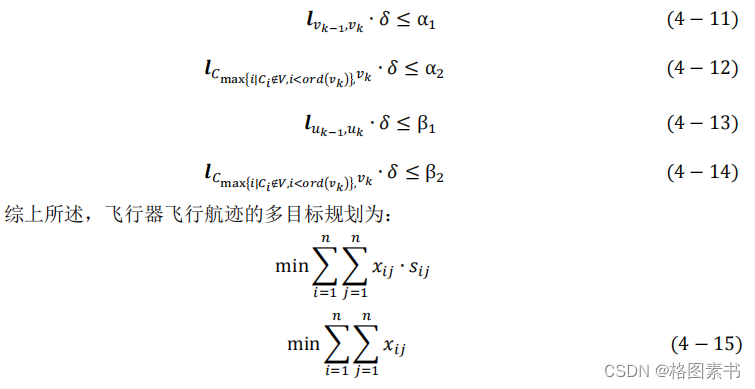

4.3 求解算法建立
针对轨迹规划问题的算法研究已经有很多的成果了,其中传统的航迹规划算法有
prim
算法,
Dijkstra
算法和动态规划方法。传统航迹规划算法适用于问题环境相对简单且规模较
小的情况,其具有运算速度快、复杂性低、有效性高,能够根据实际问题快速给出最优解
等优点,应用范围广泛而被广泛使用。针对多目标航迹规划问题,本文使用多阶段 Dijkstra
算法求解,算法的最大迭代次数为 1440 次,最长执行时间为 42.23S,由此可见,该算法
时间复杂度较低。其具体方法如下:
4.3.1 最短路径数学表达

4.3.2 自适应改进型 Dijkstra 算法求解步骤
轨迹规划问题的常用算法根据解法思想条件可以主要分为传统算法和近代优化算法
两类,其中传统的航迹规划算法有
prim
算法,
Dijkstra
算法和动态规划方法。传统航迹规
划算法适用于问题环境相对直接情况,其具有运算速度快、复杂性低、有效性高,适用范
围广的特点,能够快速根据实际问题得出结果。
传统的航迹规划算法
Dijkstra
算法具有有效性高和较强的全局搜索能力。本文在
Dijkstra
算法原理的基础上进行自适应改进,求解情况复杂的多目标优化问题中,并将改进
自适应的
Dijkstra
算法作为求解的本题适用算法。

4.3.3 自适应基于蚁群算法的飞行器航迹规划求解
蚁群算法作为一种近现代优化算法,和绝大部分的现代近似优化算法一样,蚁群算法
也是基于自然规律或者人体基因遗传进化原理而来的算法。蚁群算法是一种用于解决复杂
组合优化问题的适当的方法,它具有鲁棒性强、适应性好、全局搜索和较好的全局最优等
优点。应用在大部分环境中有较好的结果。
蚁群算法的算法思想是基于蚁群在自然界中能够在未知的条件下找到从巢穴到食物
源的最短路径的寻优原理。通过一种正反馈机制,不断将搜索方向趋于最短路径上。本
文根据基于蚁群算法的搜索原理,不断调整搜索起点 A 到终点 B 的满足优化约束条件的
路径,并根据正反馈机制,最终找到从起点 A 到终点 B,均匀经过水平和垂直校正节点的
最短路径,实现飞行器航迹规划求解。
蚁群算法原理可以表述如下:
Step1
:路径构建。
在算法的初始时刻,将
m
只蚂蚁随机的放在
n
个城市中,同时,将每只蚂蚁的搜索禁
忌表
tabu
的第一个元素设置为它当前所在城市。此时各路径上的信息素量相等,设
τ𝑖𝑗(0) =


基本蚁群算法的具体实现步骤如下: 
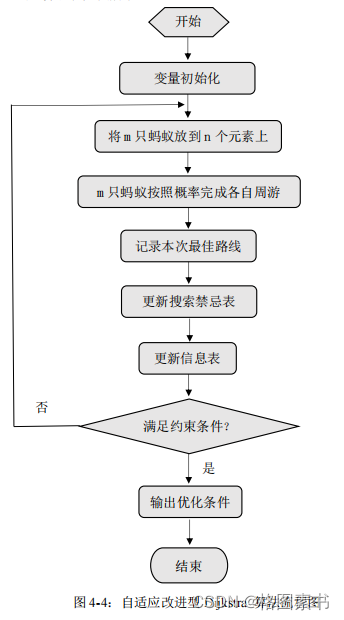
4.4 模型求解及结果分析
根据以上建立的多目标优化模型和自适应改进型算法,得到结果如下(程序见附件)。
附件一:
附件一中共有
610
个校正节点,其中水平校正节点 306 个,垂直校正节点 305 个。
在通过自适应改进 Dijkstra 算法和蚁群算法得到的最优航行轨迹的基础上,通过贪婪便利
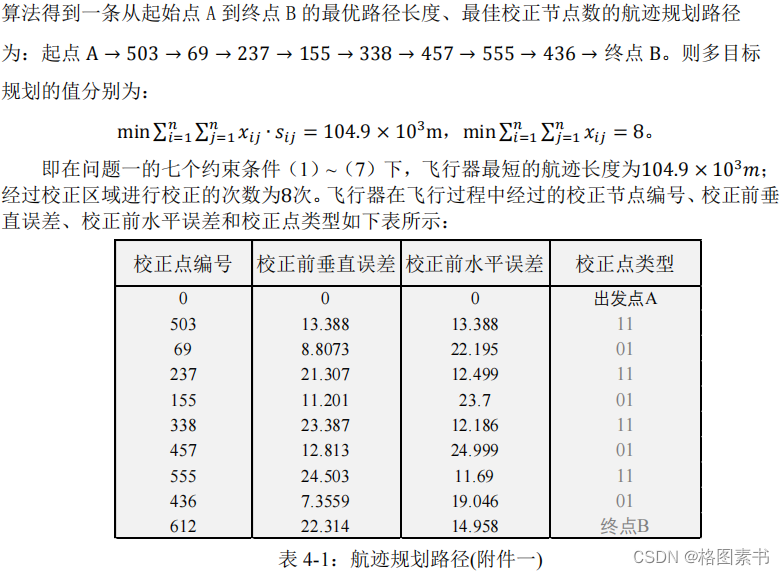

该路径经过
8
个校正点,总路程为
104.9
公里,算法迭代次数为
425
次,执行时间为
23.25S。飞行器的最优航迹规划路径如下图所示:
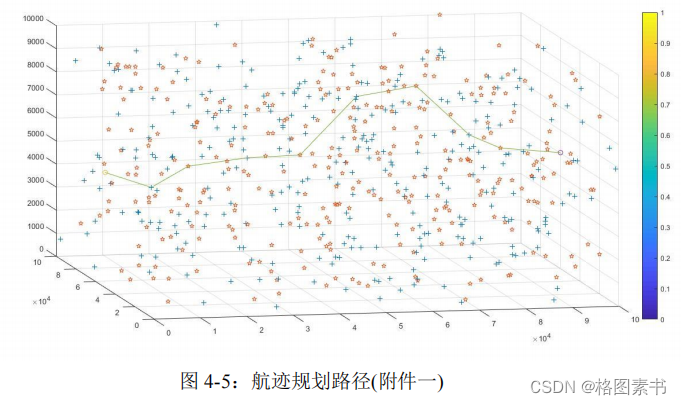

附件二:
附件二中共有
325
个校正节点,其中水平校正节点
167
个,垂直校正节点
158
个。
在通过自适应改进
Dijkstra
算法和蚁群算法得到的最优航行轨迹的基础上,通过贪婪便利
算法综合实际情况得到一条从起始点A到终点
B的最优路径长度、最佳校正节点数的航
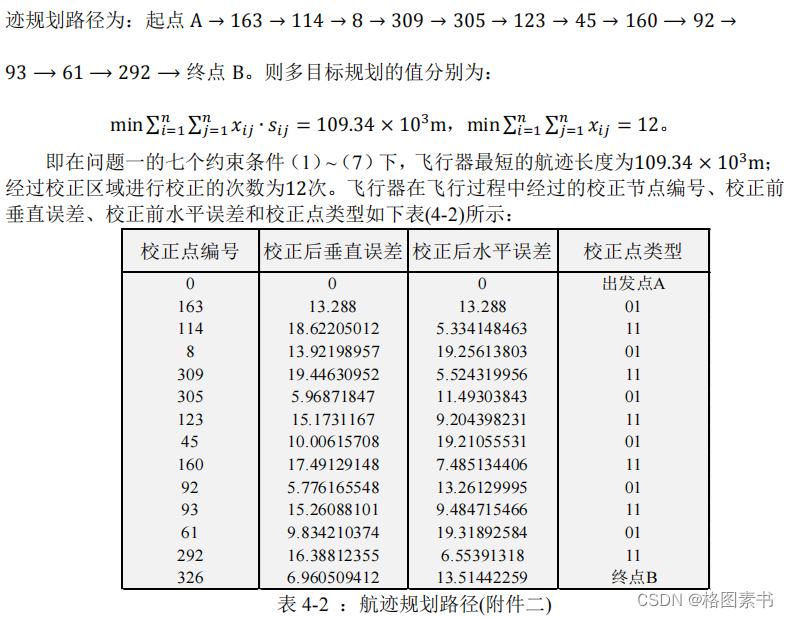

该路径经过
12
个校正点,总路程为
109.34
公里。算法迭代次数为
92
次,执行时间为
42.23S
。
飞行器的最优航迹规划路径如下图所示:
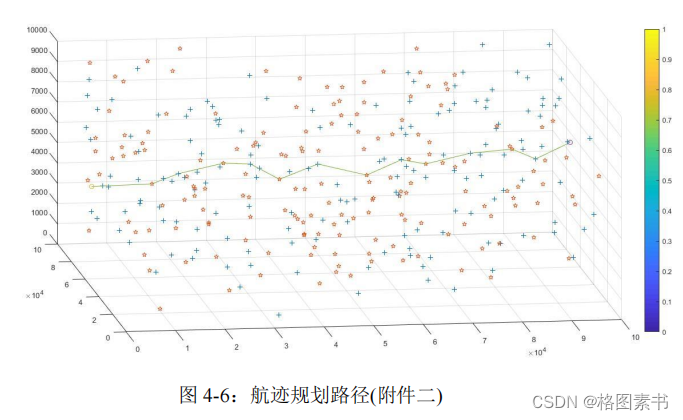

五、问题二
5.1 问题描述与分析
问题二是在问题一的飞行误差补偿约束条件的基础上,考虑飞行器在实际飞行过程中
的
200
米的最小转弯半径,实现航行轨迹的重新规划。要针对附件
1
和附件
2
中的校正节
点位置和校正节点类型,从
A
点出发到达目的地
B
点,建模规划满足约束条件(
1
)
~
(
8
)
时飞行器的航行轨迹,并且综合考虑以下优化目标:(
A
)航迹长度尽可能小;(
B
)经过
校正区域进行校正的次数尽可能少,并讨论算法的有效性和复杂度
。
约束条件中的误差补偿阈值同问题一。
其中附件
1
数据的参数为
 点。我们通过建模选择最优路线和最佳误差点数量和。
点。我们通过建模选择最优路线和最佳误差点数量和。
(
4
)根据最优路线和最佳误差点数量和带入实际问题中综合考虑多目标规划问题的最优
解。
(
5
)应用不同算法,应用自适应改进型
Dijkstra
算法与基于蚁群寻优的智能优化蚁群算法
在解决组合优化问题,通过调整数据,应用贪婪算法对航行轨迹进一步优化。
5.2 模型建立
5.2.1 飞行器转弯过程分析
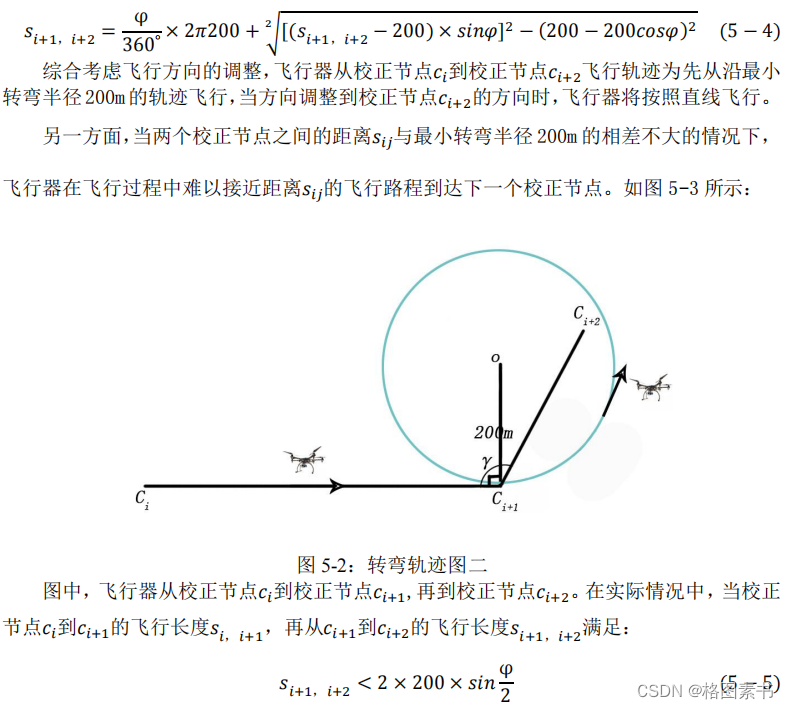
问题二是在问题一的飞行误差补偿约束条件的基础上,增加考虑实际飞行过程中,飞
行器在转弯过程中存在
200
米的最小转弯半径约束。一方面在问题一中飞行器能够直线到
达的校正节点,问题二中飞行器需要有一个飞行方向调整,最小转弯半径轨迹为一个半径
为 200m 的弧。如图所示:
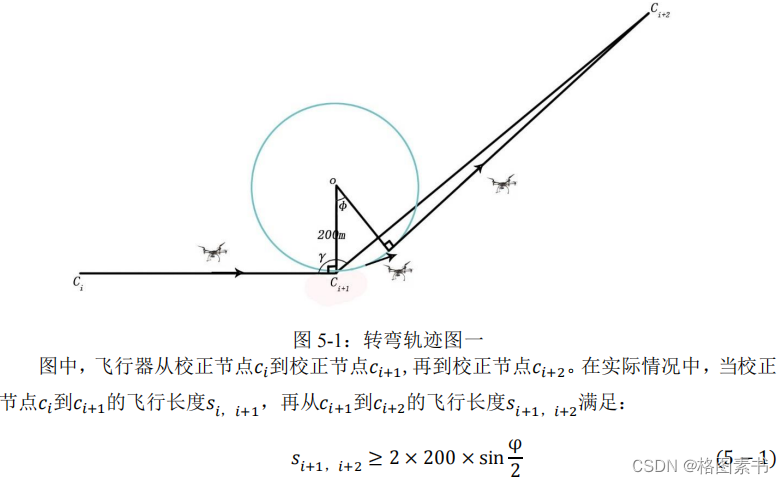

 时,飞行器将不再能够按照 200m的最小转弯半径调整飞行方向。在这种情况下,飞行器将按照更大的转弯半径,绕更大的弧形轨迹并中转更多的校正节点才能到达
时,飞行器将不再能够按照 200m的最小转弯半径调整飞行方向。在这种情况下,飞行器将按照更大的转弯半径,绕更大的弧形轨迹并中转更多的校正节点才能到达
校正节点𝑐𝑖+2
,不满足最优的路径和最佳的误差补偿点数。本文假设此种情况为不能够到达。
5.2.2 最小转弯半径约束
飞行器在实际飞行过程中,转弯时受到结构和控制系统的限制,无法完成即时转弯
(
飞
行器前进方向无法突然改变
)
,飞行器在从一个误差校正点到下一个误差校正点的过程中需
要调整飞行方向,具体情况如以上分析。则飞行器的最小转弯半径约束为:


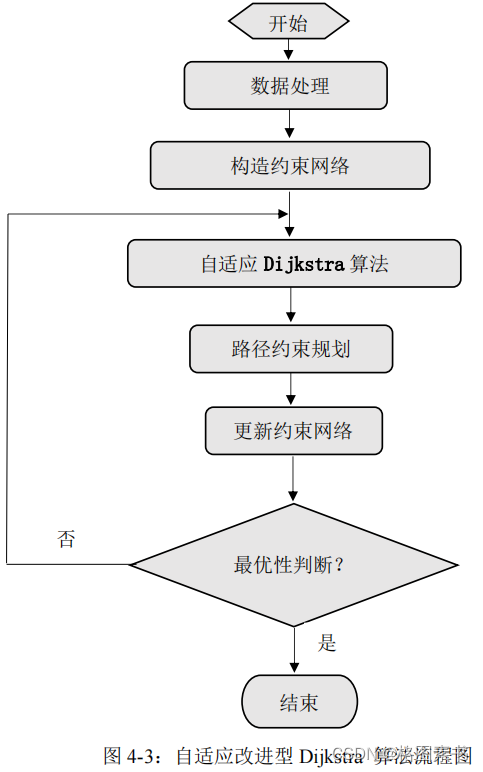
5.3 算法流程
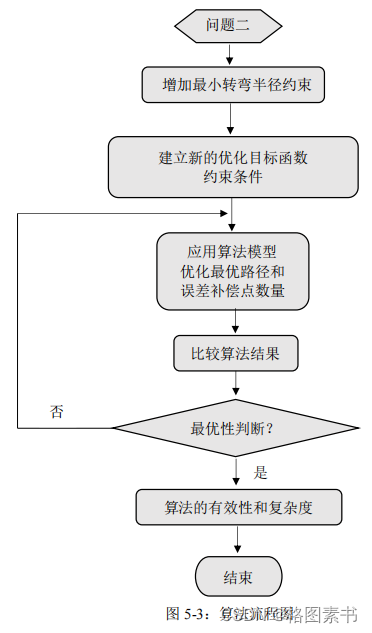
5.4 模型求解
根据以上建立的多目标优化模型,应用问题一中的自适应改进型算法,得到结果如下。
附件一:
通过应用问题一中的自适应改进
Dijkstra
算法和蚁群算法得到的最优航行轨迹的基础
上,通过贪婪便利算法综合考虑实际情况得到一条从起始点A 到终点B 的最优路径长
 即在问题二的八个约束条件(1)~(
8
)下,飞行器
最短的
航迹长度为
104.903 ×
即在问题二的八个约束条件(1)~(
8
)下,飞行器
最短的
航迹长度为
104.903 ×
经过校正区域进行校正的次数为
8
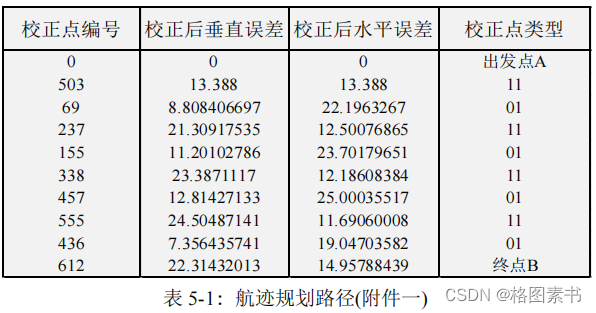
次。飞行器在飞行过程中经过的校正节点编号、
校正前垂直误差、校正前水平误差和校正点
类型
如下表
所示:
 该路径经过 8 个校正点,总路程为
104.903
公里。算法迭代次数为
425
次,执行时间
该路径经过 8 个校正点,总路程为
104.903
公里。算法迭代次数为
425
次,执行时间
为
23.25S
。
飞行器的最优航迹规划路径如下图所示:
 附件二:
附件二:
针对附件二中的校正节点坐标的类型数据,通过应用问题一中的自适应改进
Dijkstra
算法和蚁群算法得到的最优航行轨迹的基础上,通过贪婪便利算法综合考虑实际情况得
到一条从起始点A到终点B的最优路径长度、最佳校正节点数的航迹规划路径为:
 即在问题二的八个约束条件(1)
~
(
8
)下,飞行器最短的航迹长度为109.464𝑚
;经
即在问题二的八个约束条件(1)
~
(
8
)下,飞行器最短的航迹长度为109.464𝑚
;经
过校正区域进行校正的次数为
12
次。飞行器在飞行过程中经过的校正节点编号、
校正前垂直误差、校正前水平误差和校正点类型如下表所示:
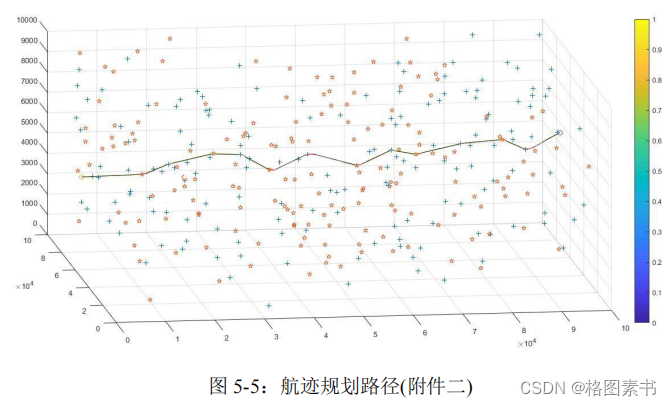
 该路径经过 12 个校正点,总路程为
109.464
公里。算法迭代次数为
92
次,执行时间
该路径经过 12 个校正点,总路程为
109.464
公里。算法迭代次数为
92
次,执行时间
为
42.23S
。
飞行器的最优航迹规划路径如下图所示:
六、问题三
6.1 问题描述与分析
问题三是在问题一的飞行误差补偿约束条件的基础上,考虑飞行器在实际飞行过程中
飞行环境可能随时间动态变化的影响。虽然最优路径和最佳误差校正点在飞行前已经确定,
但飞行器在部分校正点进行误差校正时存在无法达到理想校正的情况。考虑部分故障校正
点能够成功将某个误差校正为
0
的概率是
80%
,如果
校正失败,则校正
后的剩余误差为
min(P
𝑖
,
5)
的情况,重新规划问题一所要求的航迹
,实现航行轨迹的重新
规划。
在综合考
虑问题一的约束条件的情况下进行多目标航迹规划,优化目标如下:
(
A
)航迹长度尽可能小;
(
B
)经过校正区域进行校正的次数尽可能少;
(
C
)要求成功到达终点的概率尽可能大;
约束条件中的误差补偿阈值同问题一。
其中附件
1
数据的参数为α
1
= 25
,
α
2= 15
,
β
1
= 20
,
β
2
= 25
,
𝜃 = 30
,
𝛿 = 0.001
附件
2
中数据的参数为:
问题
α
1
= 20
,
α
2
= 10
,
β
1
= 15
,
β
2
= 20
,
𝜃 = 20
,
𝛿 = 0.001
三在增加部分可能发生误差校正故障点的基础上,重新规划航行轨迹
使得航迹路程尽可能小、经过校正区域进行校正的次数尽可能少的同时,要求成功到达终点的概率尽
可能大。即为多目标动态规划问题。根据题目和参考文献,给出新的飞行器轨迹规划策略
如下:
(
1
)约束调整:增加考虑飞行器在实际飞行中经过误差校正故障点未能进行完全误差修正
的条件约束。在问题一中飞行器能够直解到达的校正节点,问题三中飞行器需要在故障点
按概率判断误差修正情况。
(
2
)考虑飞行器在飞行过程中,经过一个误差修正点发生故障,未能完全修正的情况下,
依旧能够在当前飞行误差的条件下完成飞行目标的概率。
(
3
)飞行器在飞行过程中需要满足飞行路程短的同时,尽可能经过少的飞行误差校正节点。
我们通过建模选择最优路线和最佳误差点数量。
(
4
)根据最优路线和最佳误差点数量和带入实际问题中,比较误差故障点和安全点,综合
考虑多目标规划问题的最优解。
(
5
)应用不同算法,应用自适应改进型
Dijkstra
算法与基于蚁群寻优的智能优化蚁群算法
在解决组合优化问题,通过调整数据,应用贪婪算法对航行轨迹进一步优化。
6.2 模型建立
6.2.1 误差校正情况分析
在飞行器的实际飞行过程中,飞行环境更加复杂多变。在问题一中经过的垂直或者水
平误差校正点时,在满足误差修正阈值的条件下,均能够达到理想的修正结果。但是在问
题三中存在部分不可控校正点存在
20%
的不能完全修正的情况。分别根据附件一、附件二
中的校正节点的故障节点标志,将故障校正点进行编号:
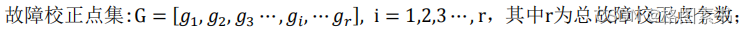
6.2.2 校正失败条件约束
问题三在问题一的基础上增加考虑飞行器在实际飞行中经过误差校正故障点未能进
行完全误差修正的条件约束。在问题一中飞行器能够直接到达的校正节点,在问题三中飞
行器需要在误差故障点按概率判断误差修正的实际情况,并根据剩余误差规划路径。


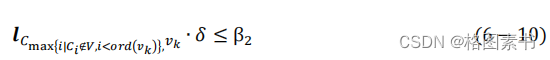 问题三的目标是在增加部分可能发生误差校正故障点的基础上,规划航行轨迹
问题三的目标是在增加部分可能发生误差校正故障点的基础上,规划航行轨迹
使得航
迹路程尽可能小、经过校正区域进行校正的次数尽可能少的同时,要求成功到达终点的概
率尽可能大。则在问题一的基础上增加成功到达终点的概率
目标函数为:

6.3 模型求解
根据以上建立的多目标优化模型,应用问题一中的自适应改进型算法,得到结果如下。
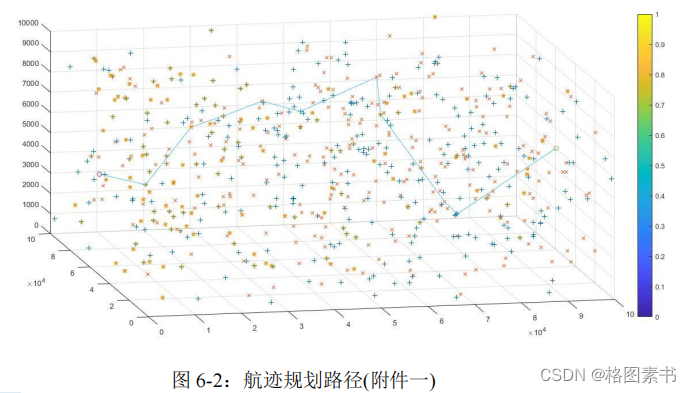
附件一:
通过应用问题一中的自适应改进
Dijkstra
算法和蚁群算法得到的最优航行轨迹的基础
上,通过贪婪便利算法在综合考虑实际情况,得到一条从起始点A 到终点B 的最优路径
 正节点编号、校正前垂直误差、校正前水平误差和校正点类型如下表所示:
正节点编号、校正前垂直误差、校正前水平误差和校正点类型如下表所示:
 该路径经过 9 个校正点,总路程为
105.77
公里。算法迭代次数为
586
次,执行时间为
该路径经过 9 个校正点,总路程为
105.77
公里。算法迭代次数为
586
次,执行时间为
13.03S
。
飞行器的最优航迹规划路径如下图所示:

附件二:
针对附件二中的校正节点坐标的类型数据,通过应用问题一中的自适应改进
Dijkstra
算法和蚁群算法得到的最优航行轨迹的基础上,通过贪婪便利算法综合考虑实际情况得
 即在问题三的七个约束条件(1)
~
(
7
)下,飞行器最短的航迹长度为
即在问题三的七个约束条件(1)
~
(
7
)下,飞行器最短的航迹长度为
155.07 × 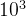 m
;
m
;
经过校正区域进行校正的次数为
21
次,成功概率为
100%
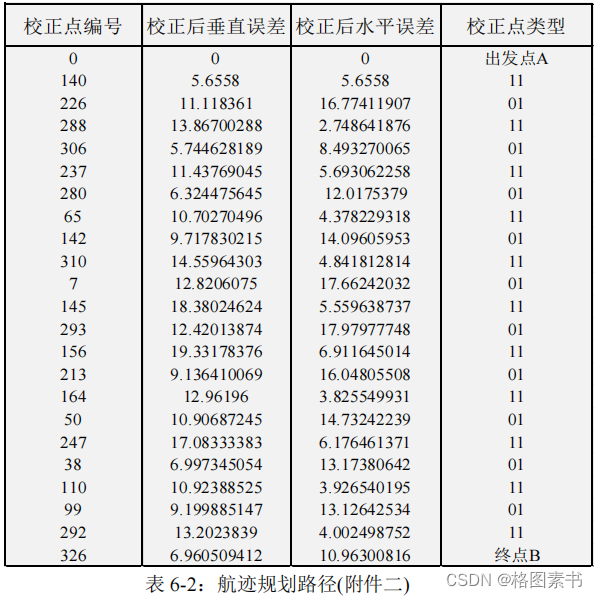
。飞行器在飞行过程中经过的校
正节点编号、校正前垂直误差、校正前水平误差和校正点类型如下表
(5-2)
所示:
针对附件二中的校正节点坐标的类型数据,算法结果为:
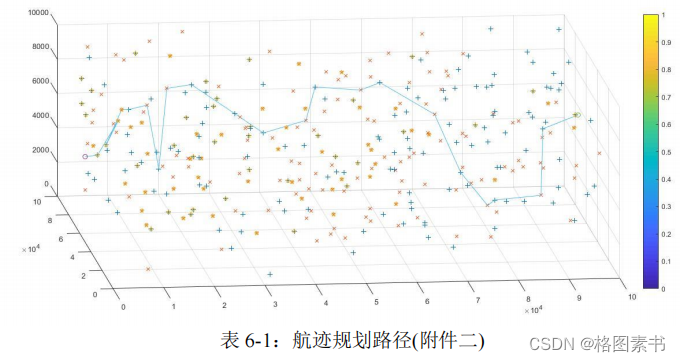
 该路径经过 21 个校正点,总路程为
155.07
公里。算法迭代次数为
1440
次,执行时间
该路径经过 21 个校正点,总路程为
155.07
公里。算法迭代次数为
1440
次,执行时间
为
5.61S
。
飞行器的最优航迹规划路径如下图所示:

根据上述结果,当飞行器的成功概率为
100%
时,飞行器需要飞行的航迹长度和需要经
过的误差补偿点个数都相对问题一有了很大增加。
根据问题一中的算法,在适当放松成功率时,飞行器的最优航迹如下:
(
1
)当成功率降低到
80%
时:从起始点A 到终点B的航迹规划路径二为:
 因此综合上述结果来看,放松成功概率的情况下,飞行器航行轨迹长度
和经过的
节点
因此综合上述结果来看,放松成功概率的情况下,飞行器航行轨迹长度
和经过的
节点
数都有相应程度的下降,在考虑飞行成功率尽可能大的情况下,我们优先选择航迹路径一。
但是在实际情况中,我们可以在相应成功率要求下,选择更优的飞行航迹路程和更佳的节
点数,即航迹路径二、三。
七、参考文献

代码实现
%%%%%%%%%%%%%%%%%%%%%%%%%
PATH=cell(10000,1);
SENDNEW=SSSNEW;
for i=1:10^4
b=sparse(SENDNEW);
[dist,path,pred] = graphshortestpath(b,1,613);
%起点 1,2,3,约束
if ismember(path(2),verticaldata)==1
if S(path(1),path(2))<=25/0.001 & S(path(1),path(2))<=15/0.001
if S(path(2),path(3))<=20/0.001 & ( S(path(1),path(2))+S(path(2),path(3)) ) <=25/0.001
path=path;
else
SENDNEW(path(2),path(3))=0;SENDNEW(path(3),path(2))=0;
%path=[];
continue;
end
else
SENDNEW(path(1),path(2))=0;SENDNEW(path(2),path(1))=0;
%path=[];
continue;
end
elseif ismember(path(2),standarddata)==1
if S(path(1),path(2))<=20/0.001 & S(path(1),path(2))<=25/0.001
if S(path(2),path(3))<=15/0.001 & (S(path(1),path(2))+S(path(2),path(3)) ) <=25/0.001
path=path;
else
SENDNEW(path(2),path(3))=0;SENDNEW(path(3),path(2))=0;
%path=[];
continue;
end
else
SENDNEW(path(1),path(2))=0;SENDNEW(path(2),path(1))=0;
%path=[];
continue;
end
end
%中间点约束
flag=0;
for m=3:length(path)-1
if ismember(path(m),verticaldata)==1
if ( S(path(m-2),path(m-1)) + S(path(m-1),path(m)) )<=25/0.001 & S(path(m-
1),path(m))<15/0.001
path=path;
else
SENDNEW(path(m-1),path(m))=0;SENDNEW(path(m),path(m-1))=0;
%path=[];
flag=1;
break;
end
elseif ismember(path(m),standarddata)==1
if (S(path(m-2),path(m-1)) + S(path(m-1),path(m)))<=25/0.001 & S(path(m-
1),path(m))<20/0.001
path=path;
else
SENDNEW(path(m-1),path(m))=0;SENDNEW(path(m),path(m-1))=0;
%path=[];
flag=1;
break;
end
end
end
if flag==1
continue;
end
%终点约束
if ( S( path(size(path,2)-2),path(size(path,2)-1) )+S( path(size(path,2)-1),613 ) )<30/0.001
path=path;
else
SENDNEW(613,path(size(path,2)-1))=0;
SENDNEW(path(size(path,2)-1),613)=0;
%path=[];
continue;
end
%交叉约束
flagbb=0;
for j=2:length(path)-1
if ( ismember(path(j),verticaldata) & ismember(path(j+1),verticaldata) ) |
( ismember(path(j),standarddata) & ismember(path(j+1),standarddata) )
SENDNEW(path(j),path(j+1))=0;
SENDNEW(path(j+1),path(j))=0;
%path=[];
flagbb=1;
break;
end
end
if flagbb==1
continue;
end
%拐弯问题 2 约束
%在误差较小时误差成功概率大
%一般角度是钝角
flagcc=0;
for nv=2:length(path)-1
cosalpha=( (S(path(nv-1),path(nv)))^2+(S(path(nv),path(nv+1)))^2-(S(path(nv-
1),path(nv+1)))^2 )/( 2*S(path(nv-1),path(nv))*S(path(nv),path(nv+1)) );
sinbeita=abs(cosalpha);
if 200*sinbeita*2<=S(path(nv),path(nv+1))
path=path;
else
SENDNEW(path(nv),path(nv+1))=0;SENDNEW(path(nv+1),path(nv))=0;
flagcc=1;
break;
end
end
if flagcc==1
continue;
end
%%%%%%%%%%%%%%%%%故障点从 3 到 n-2 个点的约束
flagdd=0;
for ok=3:length(path)-3
if ismember(path(ok),wrong_point)
if S(path(ok),path(ok+1))+S(path(ok+1),path(ok+2))<=20/0.001
path=path;
else
SENDNEW(path(ok),path(ok+1))=0;SENDNEW(path(ok+1),path(ok))=0;
flagdd=1;
break;
end
end
end
if flagdd==1
continue;
end
%%%%%%%%%%%%%故障点在 n-2 点的约束
%if S(path(length(path)-2),path(length(path)-1))+S(path(length(path)-
1),path(length(path)))<25/0.001
% path=path;
%else
% SENDNEW(path(length(path)-2),path(length(path)-1))=0;SENDNEW(path(length(path)-
1),path(length(path)-2))=0;
%continue;
%end
%最优路径的故障点保存
wrong_save=[];
for okj=1:length(path)
if ismember(path(okj),wrong_point)
wrong_save=[wrong_save,okj];%
end
end
%能到达这里的 path 这里已经经过了重重考验
PATH{i}=path;
countt=0;
for k=1:size(PATH,1)
countt=countt+~isempty(PATH{k});
end
if countt~=0
break;
end
end