介绍stack_queue及OJ题
- 前言
- 一、简单了解
- 1、stack
- 2、queue
- 二、OJ题(前三个栈,第四、五个队列)
- 1、最小栈
- (1)题目描述
- (2)解题思路
- (3)解题代码
- 2、栈的压入、弹出序列
- (1)题目描述
- (2)解题思路
- (3)解题代码
- 3、逆波兰表达式求值
- (1)题目描述
- (2)解题思路
- (3)补充小知识:中缀转后缀运算
- i、场景一:最简单
- ii、场景二:出现括号
- iii、场景三:连续比较
- (4)解题代码
- 4、二叉树的层序遍历1
- (1)题目描述
- (2)解题思路
- (3)解题代码
- 5、二叉树的层序遍历2
- (1)题目描述
- (2)解题思路
- (3)解题代码
- 三、容器适配器
- 1、什么是适配器
- 2、模拟实现stack容器适配器
- 3、模拟实现queue容器适配器
- 4、介绍deque(外强中干)
- (1)deque的原理介绍
- (2)了解一下vector和list的优势和缺陷
- (3)中控数组概念
- i、与vector比较
- ii、与list比较
- (4)简单介绍deque的底层
- (5)deque缺陷
- (6)为什么选择deque作为stack和queue的底层默认容器
前言
简单的stack_queue操作起来和模拟起来很简单,但是其中蕴含的逻辑需要仔细甄别,特别是要根据STL库函数中的代码进行理解起来就稍微有些难以理解,所以我们需要一边利用着源代码一边利用着数据结构的知识进行操作理解。
一、简单了解
1、stack

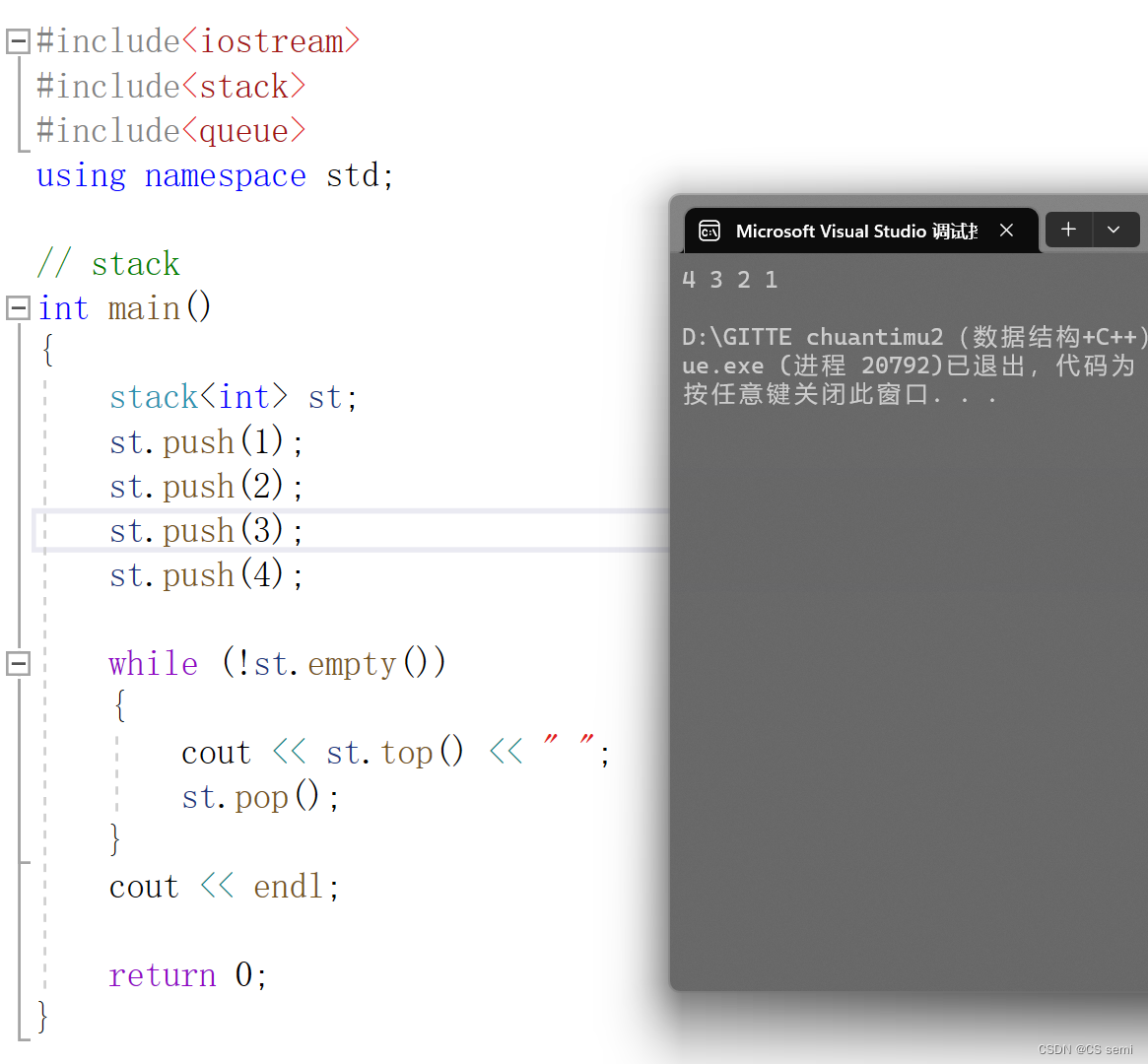
#include<iostream>
#include<stack>
#include<queue>
using namespace std;
// stack
int main()
{
stack<int> st;
st.push(1);
st.push(2);
st.push(3);
st.push(4);
while (!st.empty())
{
cout << st.top() << " ";
st.pop();
}
cout << endl;
return 0;
}
2、queue

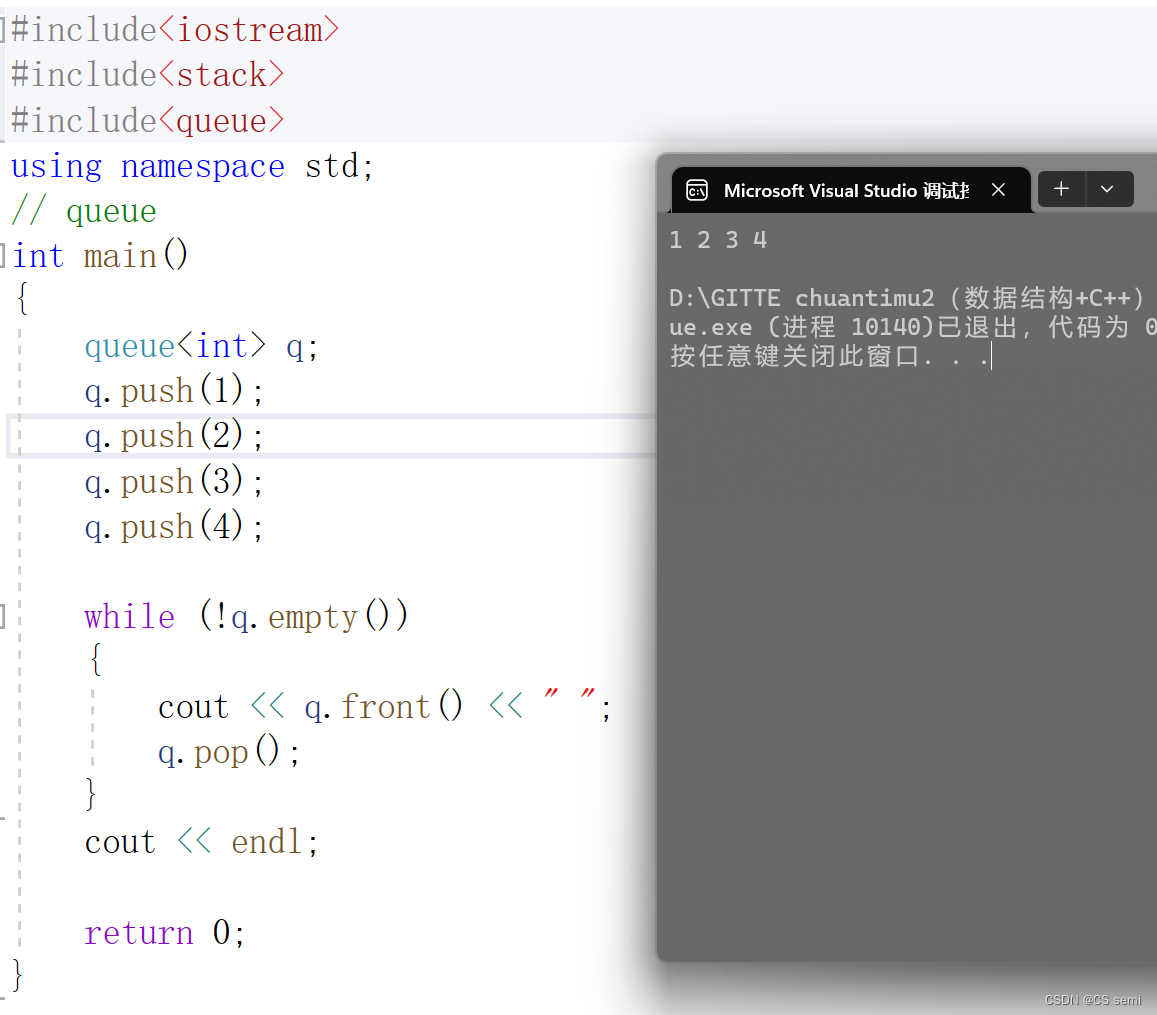
#include<iostream>
#include<stack>
#include<queue>
using namespace std;
// queue
int main()
{
queue<int> q;
q.push(1);
q.push(2);
q.push(3);
q.push(4);
while (!q.empty())
{
cout << q.front() << " ";
q.pop();
}
cout << endl;
return 0;
}
二、OJ题(前三个栈,第四、五个队列)
1、最小栈
(1)题目描述
leetcode最小栈
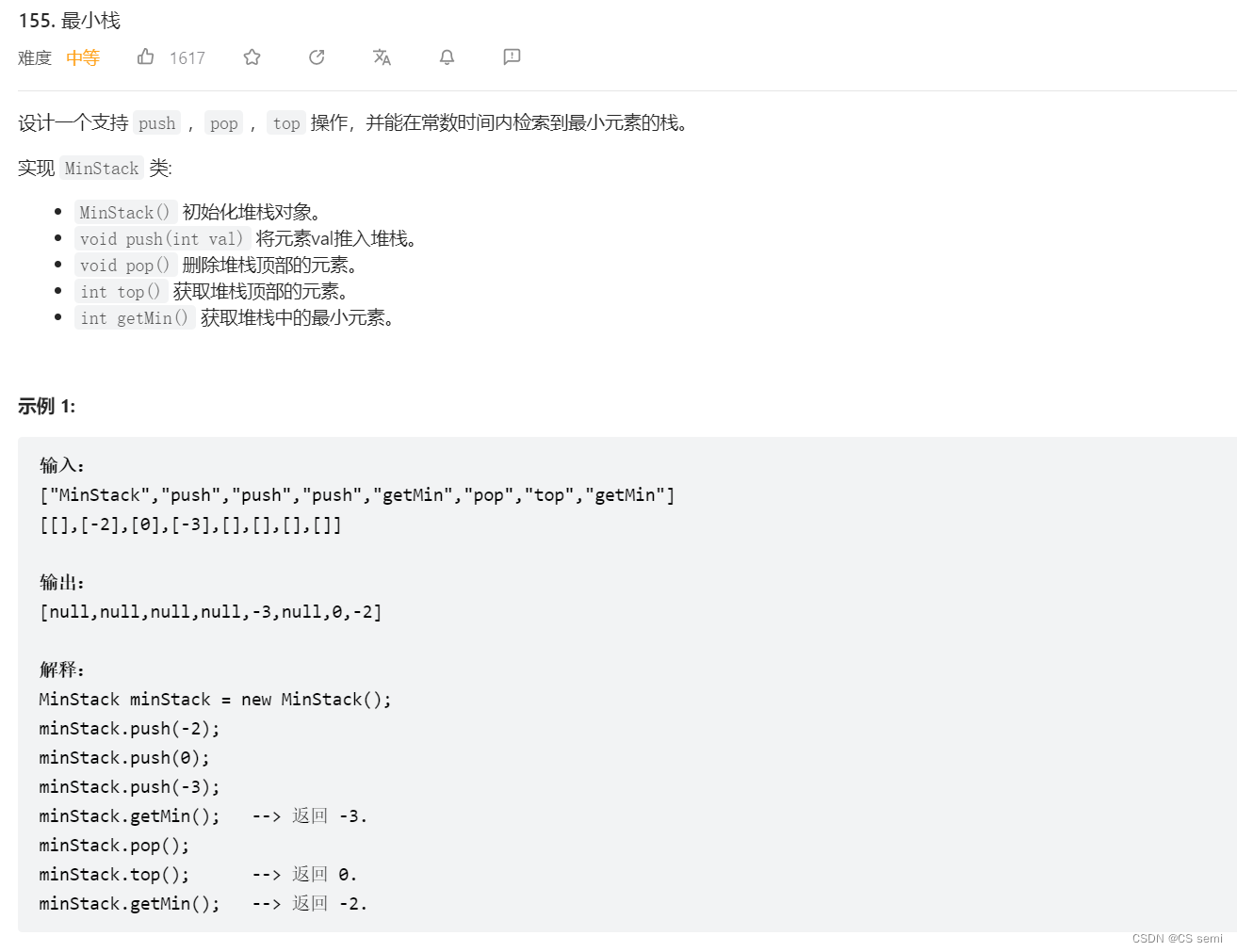
接口函数:
class MinStack {
public:
MinStack() {
}
void push(int val) {
}
void pop() {
}
int top() {
}
int getMin() {
}
};
(2)解题思路
利用两个栈,一个栈是正常栈,另一个栈是最小栈,正常栈里面存放的是所有的值,最小栈里面存放的是与底下元素进行比较,较小的存放进去,较大的不存放。
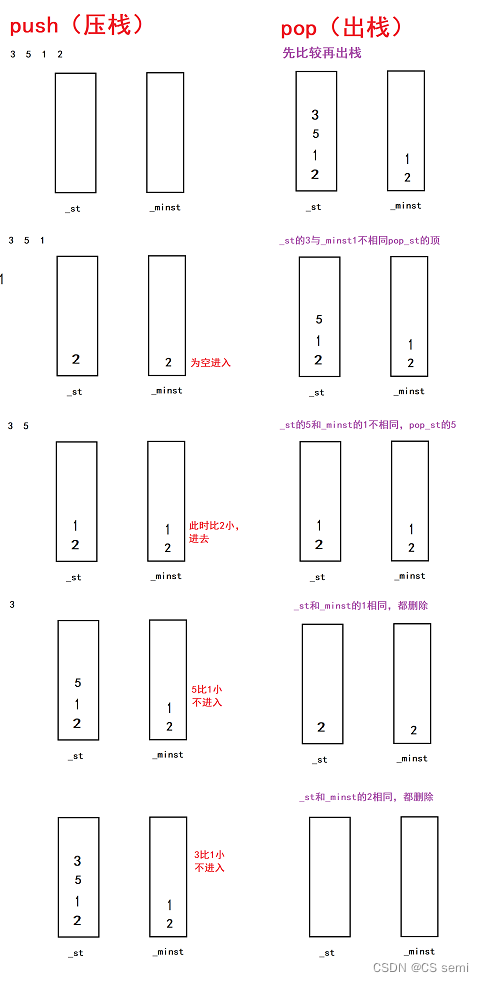
(3)解题代码
class MinStack {
public:
MinStack() {}
void push(int val) {
_st.push(val);
if(_minst.empty() || val <= _minst.top())
{
_minst.push(val);
}
}
void pop() {
if(_minst.top() == _st.top())
{
_minst.pop();
}
_st.pop();
}
int top() {
return _st.top();
}
int getMin() {
return _minst.top();
}
private:
stack<int> _st;
stack<int> _minst;
};
2、栈的压入、弹出序列
(1)题目描述
牛客网栈的压入、弹出序列

(2)解题思路
模拟!
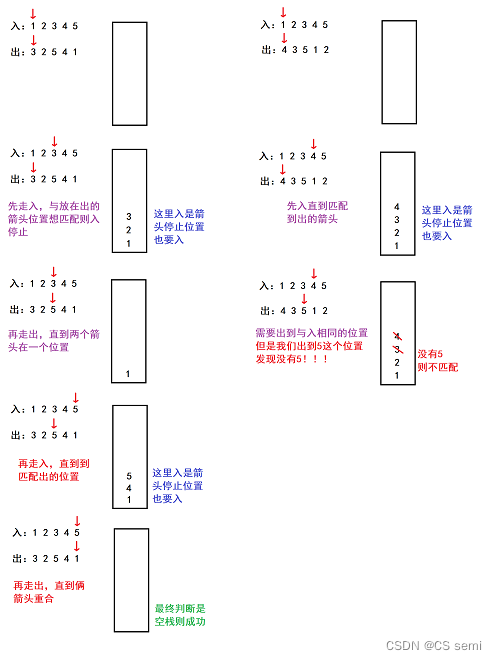
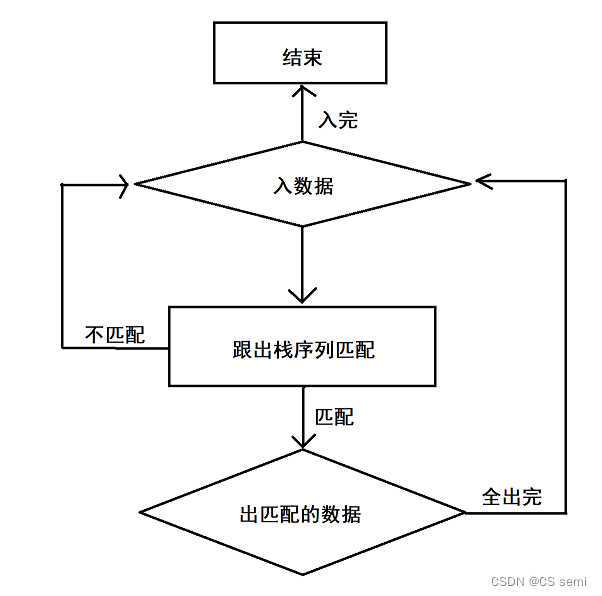
(3)解题代码
class Solution {
public:
bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {
stack<int> st;
int pushi = 0;
int popi = 0;
while(pushi < pushV.size())
{
st.push(pushV[pushi++]);
// 不匹配
if(st.top() != popV[popi])
{
continue;
}
// 匹配
else
{
while(!st.empty() && st.top() == popV[popi])
{
st.pop();
++popi;
}
}
}
return st.empty();
}
};
3、逆波兰表达式求值
(1)题目描述
leetcode逆波兰表达式求值

(2)解题思路
利用后缀进行计算如下:
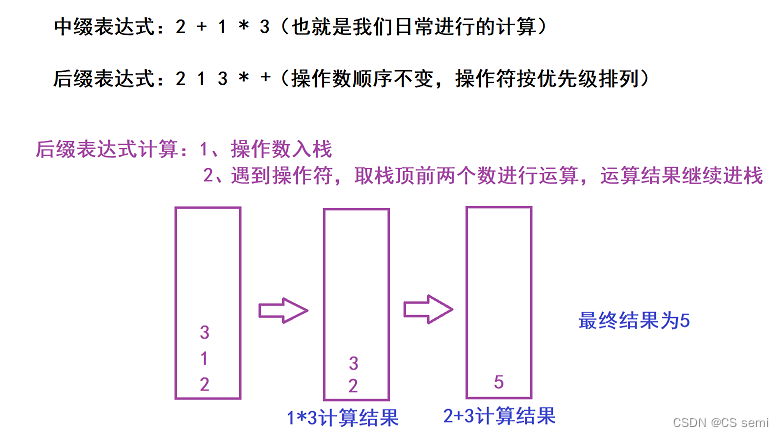
(3)补充小知识:中缀转后缀运算

i、场景一:最简单
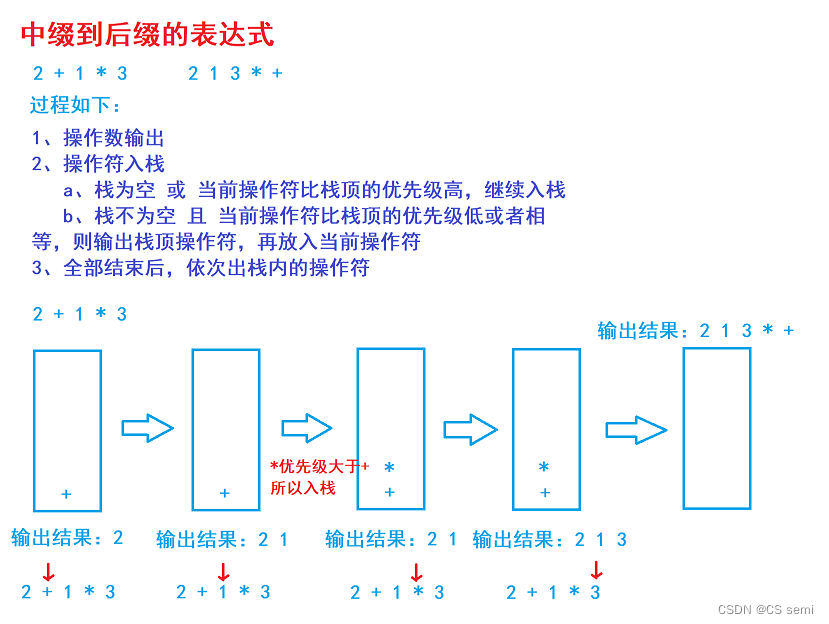
ii、场景二:出现括号
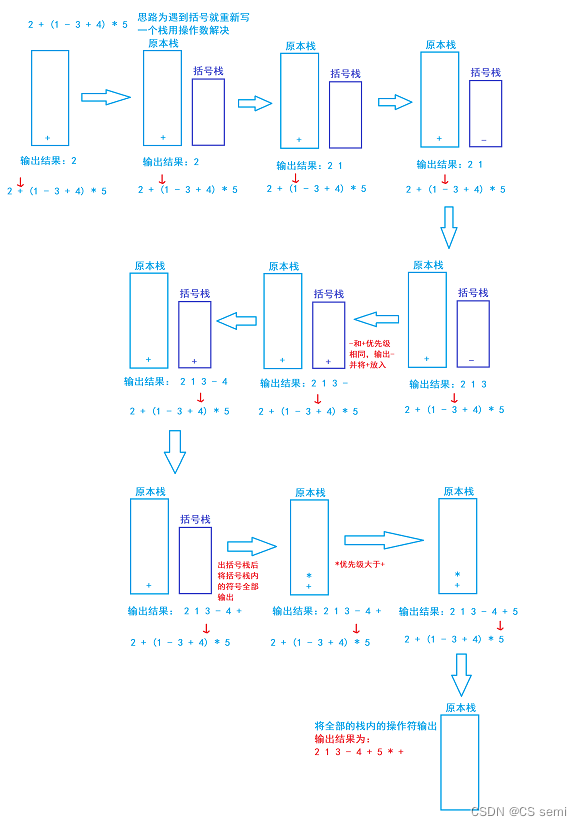
iii、场景三:连续比较
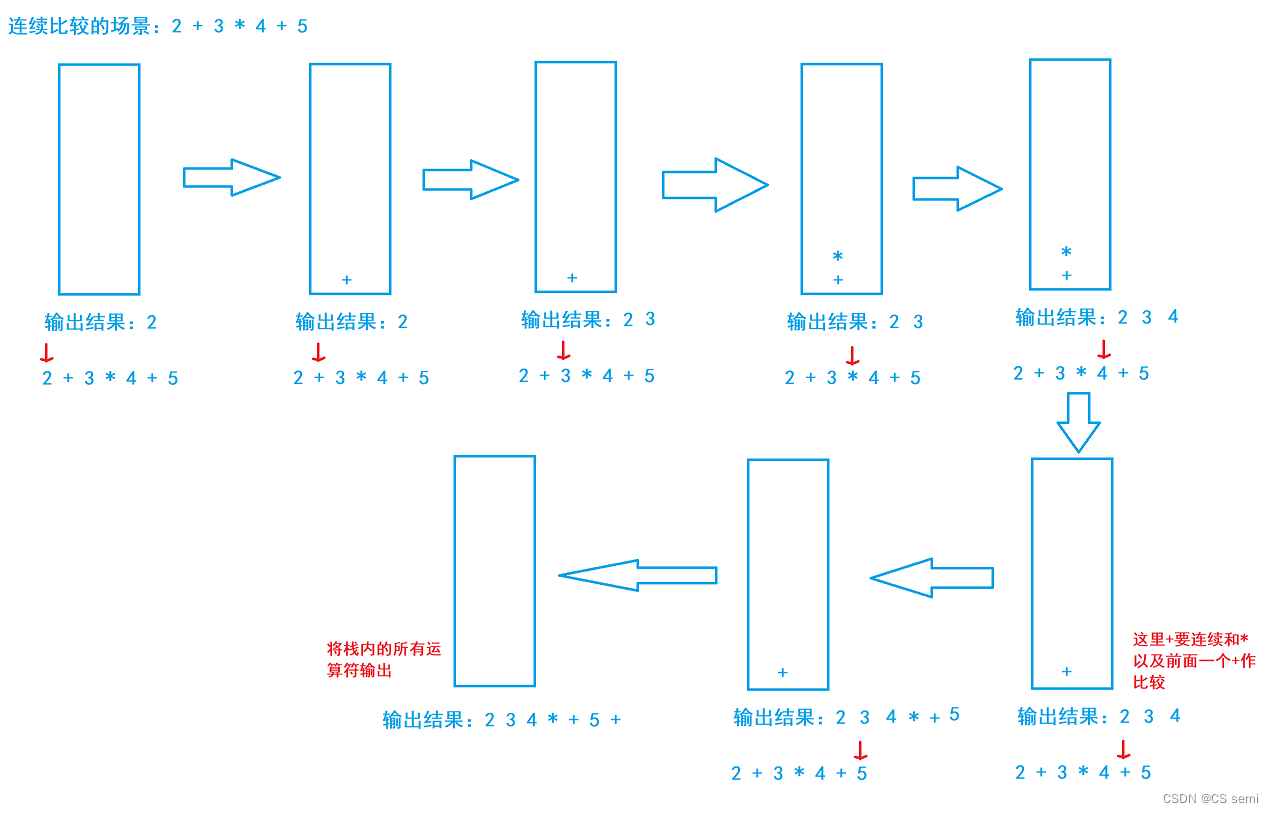
(4)解题代码
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> st;
for(auto& str : tokens)
{
if(str == "+" || str == "-" || str == "*" || str == "/")
{
int right = st.top();
st.pop();
int left = st.top();
st.pop();
switch(str[0])
{
case '+':
{
st.push(left+right);
break;
}
case '-':
{
st.push(left-right);
break;
}
case '*':
{
st.push(left*right);
break;
}
case '/':
{
st.push(left/right);
break;
}
}
}
else
{
st.push(stoi(str));
}
}
return st.top();
}
};
4、二叉树的层序遍历1
(1)题目描述
leetcode二叉树的层序遍历
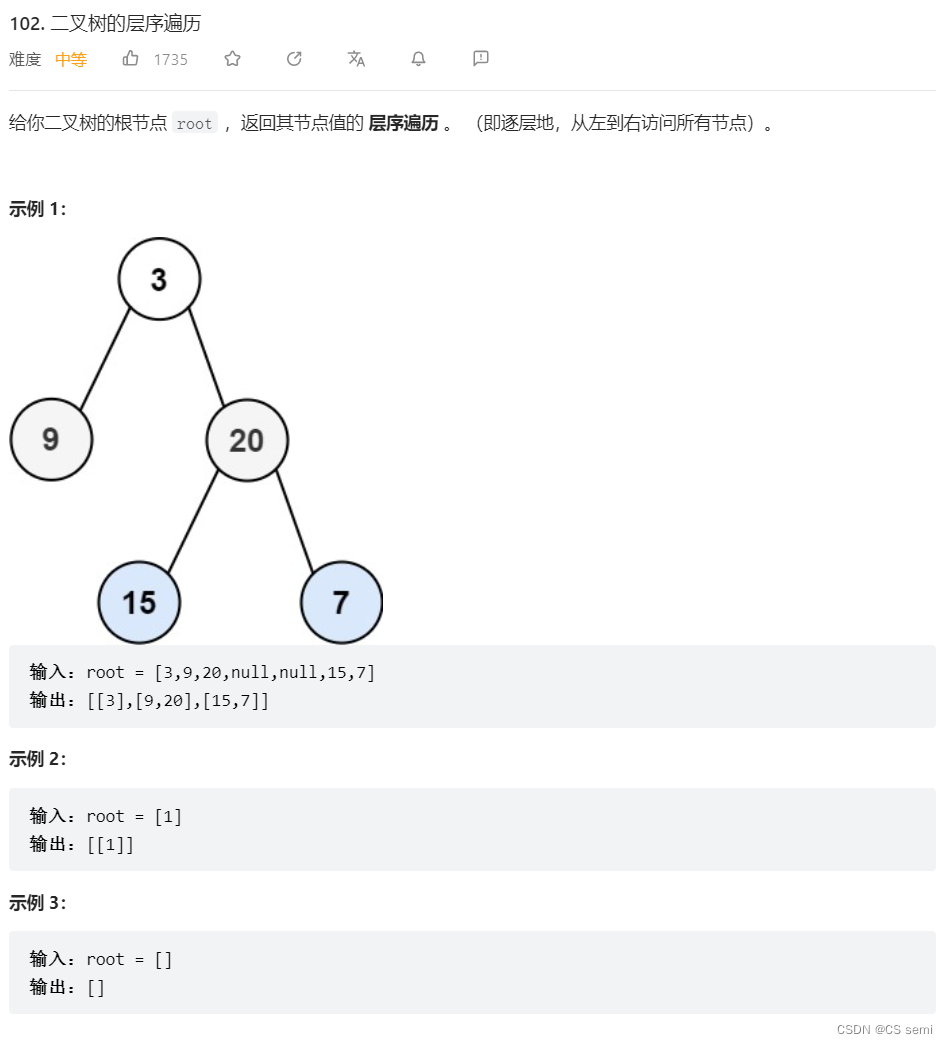
(2)解题思路
加一个LevelSize,记录每一层的数量,出一个往外减减,需要特别注意的是出一个进其二叉树底下的结点(两个或一个)。
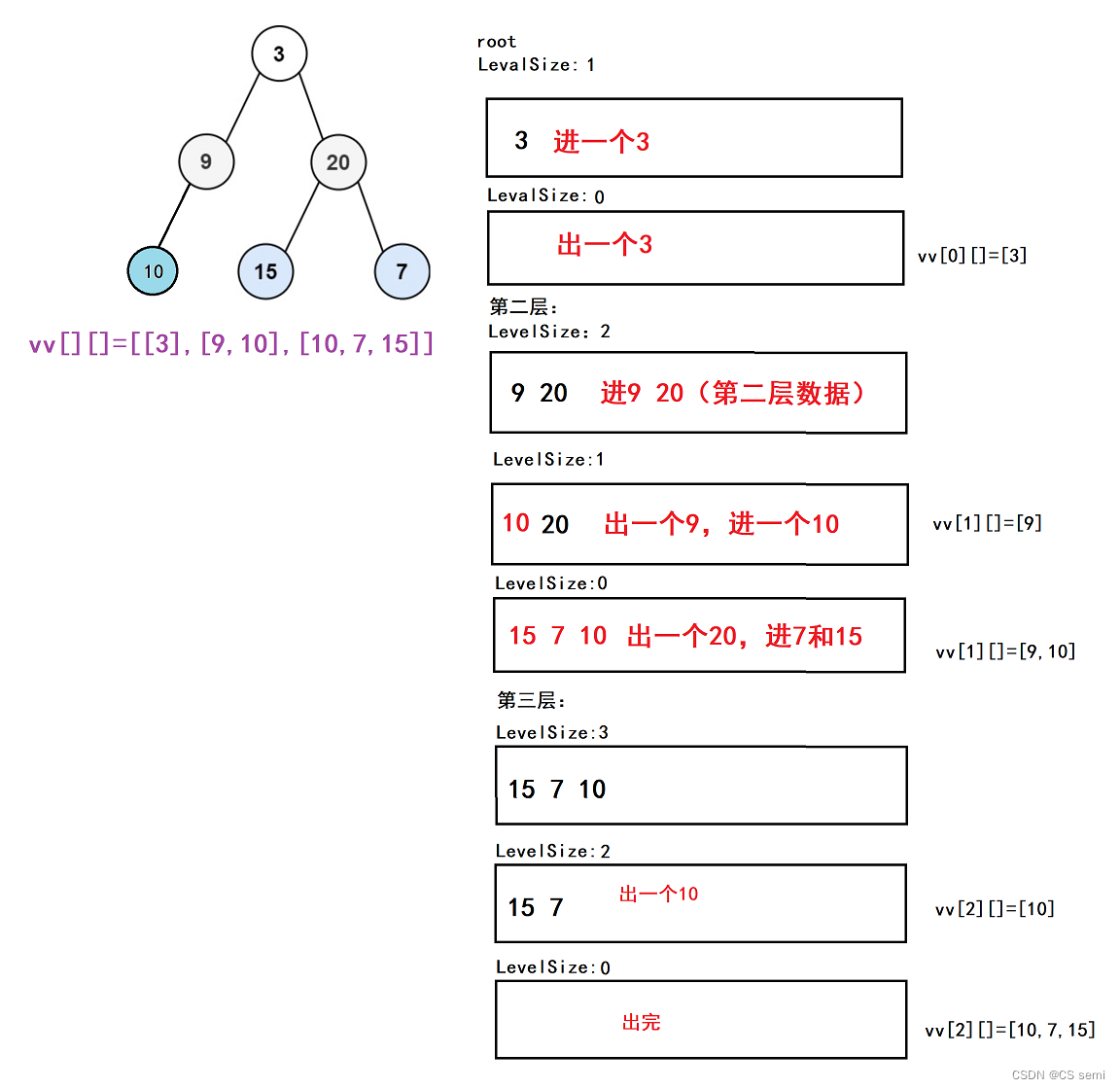
(3)解题代码
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> vv;
queue<TreeNode*> q;
int LevelSize = 0;
if(root)
{
q.push(root);
LevelSize = 1;
}
while(!q.empty())
{
vector<int> v;
for(int i = 0; i < LevelSize; ++i)
{
TreeNode* front = q.front();
q.pop();
v.push_back(front->val);
if(front->left)
q.push(front->left);
if(front->right)
q.push(front->right);
}
vv.push_back(v);
LevelSize = q.size();
}
return vv;
}
};
5、二叉树的层序遍历2
(1)题目描述
leetcode二叉树的层序遍历2
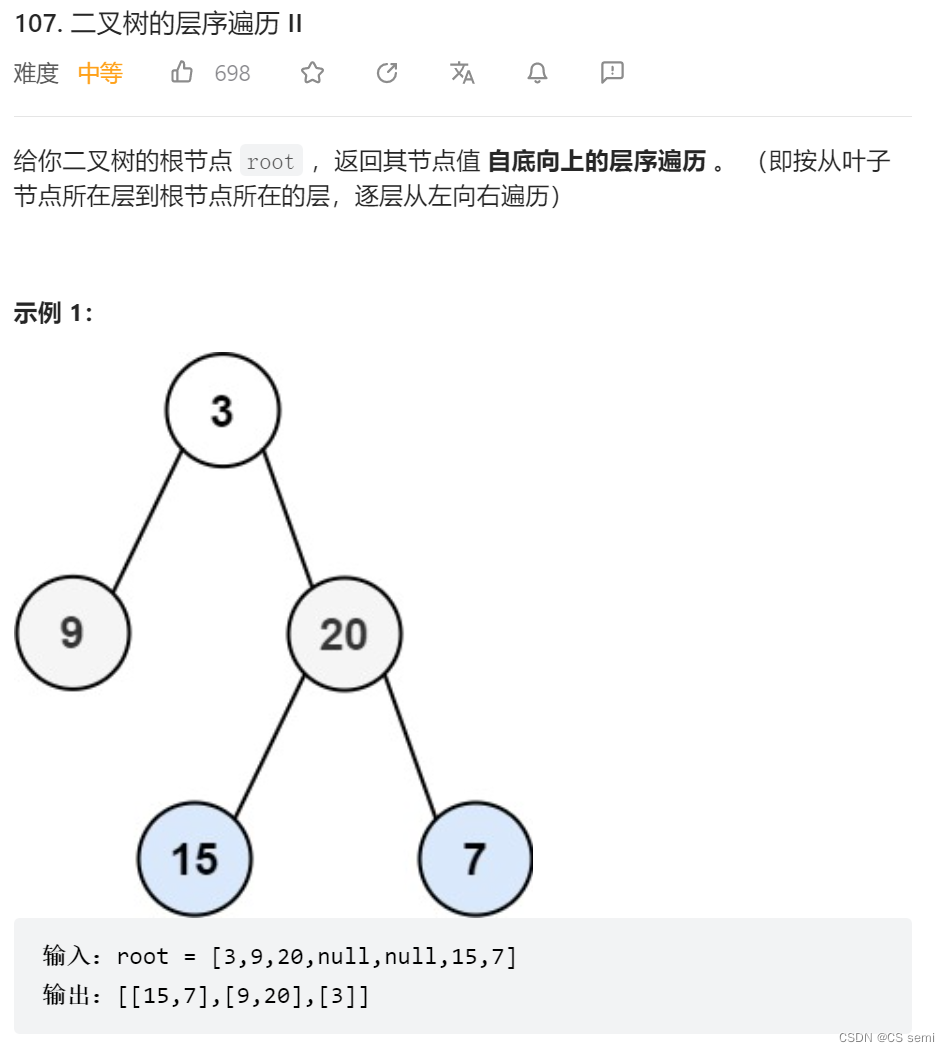
(2)解题思路
只用加一个reverse即可,因为是从下往上遍历的。
(3)解题代码
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
vector<vector<int>> vv;
queue<TreeNode*> q;
int LevelSize = 0;
if(root)
{
q.push(root);
LevelSize = 1;
}
while(!q.empty())
{
vector<int> v;
for(int i = 0; i < LevelSize; ++i)
{
TreeNode* front = q.front();
q.pop();
v.push_back(front->val);
if(front->left)
q.push(front->left);
if(front->right)
q.push(front->right);
}
vv.push_back(v);
LevelSize = q.size();
}
reverse(vv.begin(), vv.end());
return vv;
}
};
三、容器适配器
1、什么是适配器
适配器是一种设计模式(设计模式是一套被反复使用的、多数人知晓的、经过分类编目的、代码设计经验的总结),该种模式是将一个类的接口转换成客户希望的另外一个接口。


deque后续介绍。
2、模拟实现stack容器适配器
stack.h:
#include<iostream>
#include<vector>
#include<list>
namespace JRH
{
// 容器适配器
template<class T, class Container = deque<T>>
class stack
{
public:
// 插入 尾插
void push(const T& x)
{
_con.push_back(x);
}
// 删除 尾删
void pop()
{
_con.pop_back();
}
// 取栈顶元素
T& top()
{
return _con.back();
}
// 输出个数
size_t size()
{
return _con.size();
}
// 判空
bool empty()
{
return _con.empty();
}
private:
Container _con;
};
void test_stack1()
{
stack<int, vector<int>> st1;
st1.push(1);
st1.push(2);
st1.push(3);
st1.push(4);
while (!st1.empty())
{
cout << st1.top() << " ";
st1.pop();
}
cout << endl;
stack<int, list<int>> st2;
st2.push(1);
st2.push(2);
st2.push(3);
st2.push(4);
while (!st2.empty())
{
cout << st2.top() << " ";
st2.pop();
}
cout << endl;
}
}
test.cpp:
#include<iostream>
#include<vector>
#include<list>
#include<queue>
#include<stack>
using namespace std;
#include"stack.h"
#include"queue.h"
int main()
{
JRH::test_stack1();
//JRH::test_queue();
return 0;
}
知识点:为什么using namespace std放在比stack.h上面?

这是因为编译器进行编译的时候是往上寻找,而上面正好是已经展开std的全局命名空间域了,也就是能直接找到了。
3、模拟实现queue容器适配器
queue.h:
namespace JRH
{
// 容器适配器
template<class T, class Container = deque<T>>
class queue
{
public:
// 插入 尾插
void push(const T& x)
{
_con.push_back(x);
}
// 删除 头删
void pop()
{
// vector没有头删 只能用这种方法
// 库中不能用vector
_con.erase(_con.begin());
//_con.front();
}
// 取队头元素
T& front()
{
return _con.front();
}
// 取队尾元素
T& back()
{
return _con.back();
}
// 输出个数
size_t size()
{
return _con.size();
}
// 判空
bool empty()
{
return _con.empty();
}
private:
Container _con;
};
void test_queue()
{
queue<int, list<int>> q;
q.push(1);
q.push(2);
q.push(3);
q.push(4);
while (!q.empty())
{
cout << q.front() << " ";
q.pop();
}
cout << endl;
}
}
test.cpp:
#include<iostream>
#include<vector>
#include<list>
#include<queue>
#include<stack>
using namespace std;
#include"stack.h"
#include"queue.h"
int main()
{
//JRH::test_stack1();
JRH::test_queue();
return 0;
}
4、介绍deque(外强中干)
(1)deque的原理介绍
**deque(双端队列):**是一种双开口的"连续"空间的数据结构,双开口的含义是:可以在头尾两端进行插入和删除操作,且时间复杂度为O(1),与vector比较,头插效率高,不需要搬移元素;与list比较,空间利用率比较高。
deque并不是真正连续的空间,而是由一段段连续的小空间拼接而成的,实际deque类似于一个动态的二维数组。
(2)了解一下vector和list的优势和缺陷
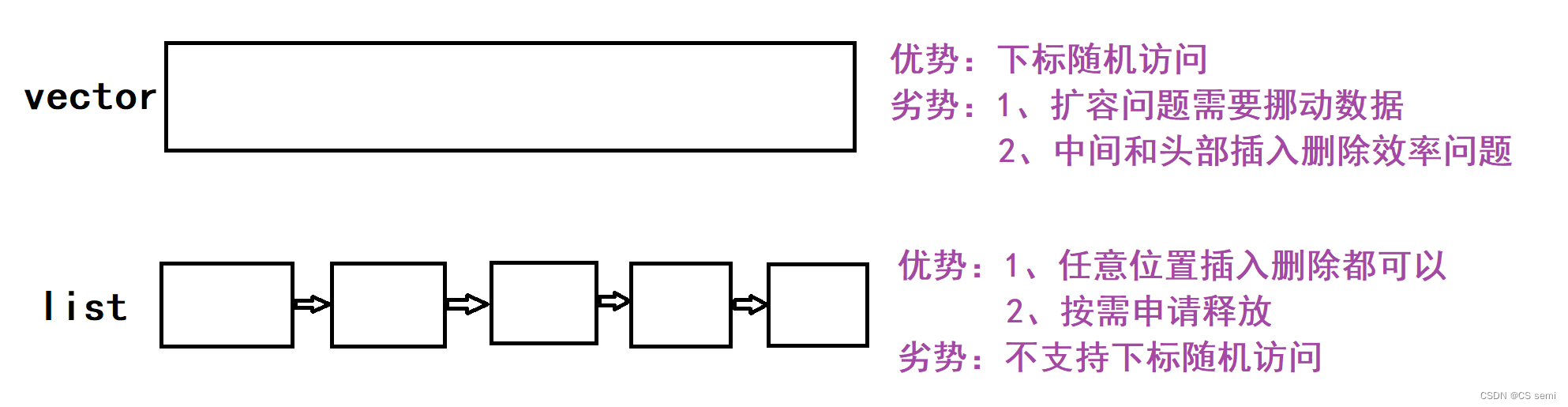
(3)中控数组概念
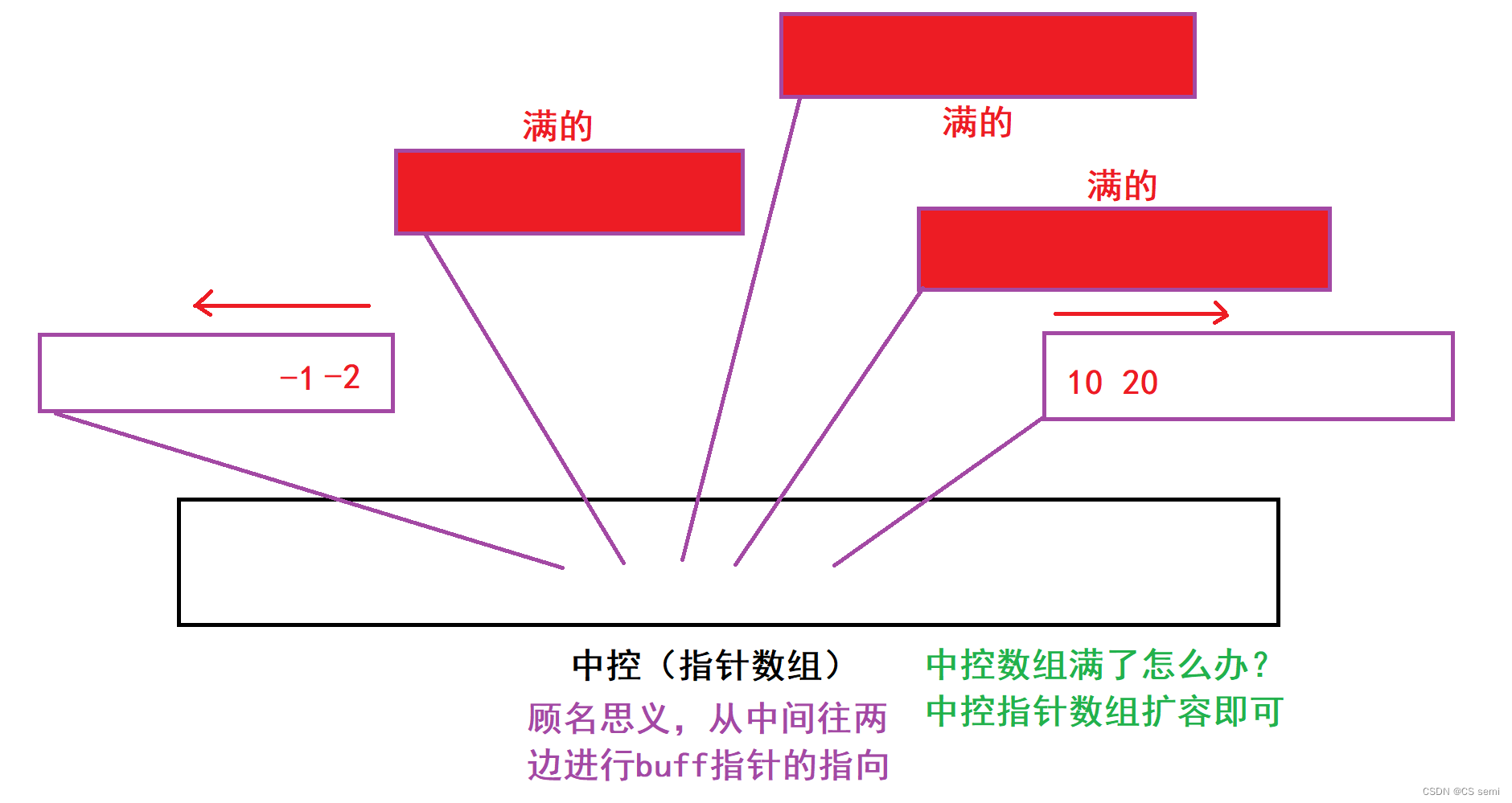
我们假设每一个指针数组指向的空间的数组的大小数量是一样的。
i、与vector比较
优势是极大缓解了扩容问题和头插头删的问题。
劣势是[]括号下标访问不够极致不够好,计算在哪个buff,在哪个buff的第几个很难,如果是高频访问[]不够好,速度慢。
计算公式:

ii、与list比较
优势是可以支持下标随机访问以及cpu高速缓存效率不错。
劣势是如果在中间插入数据的话怎么办?如果我们选择挪动数据,那么操作量也太大了,如果我们选择扩容,那么计算在哪个buff就变得很难了。
(4)简单介绍deque的底层
双端队列底层是一段假象的连续空间,实际是分段连续的,为了维护其“整体连续”以及随机访问的假象,落在了deque的迭代器身上,因此deque的迭代器设计就比较复杂,如下图所示:
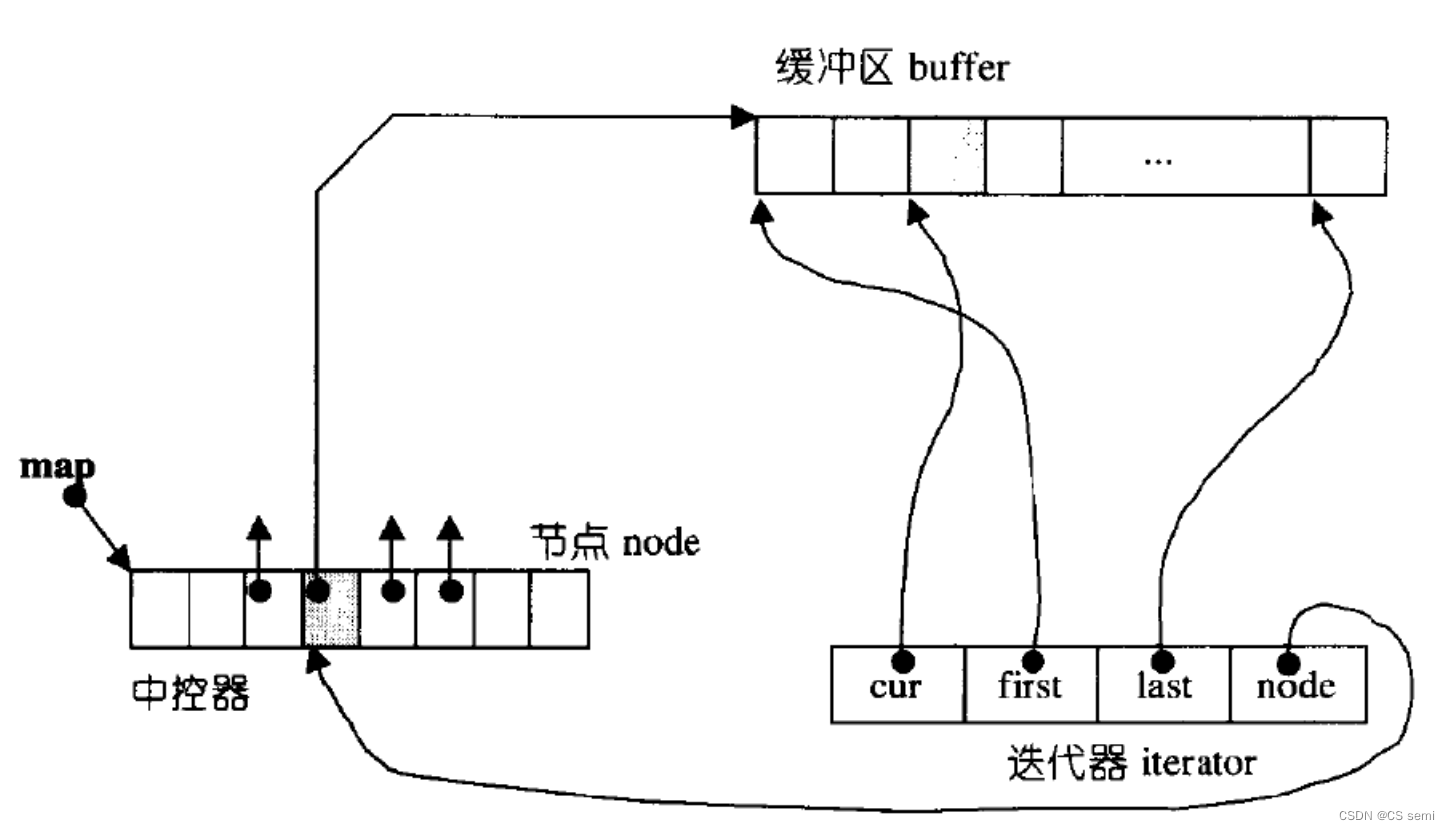
连续节奏:
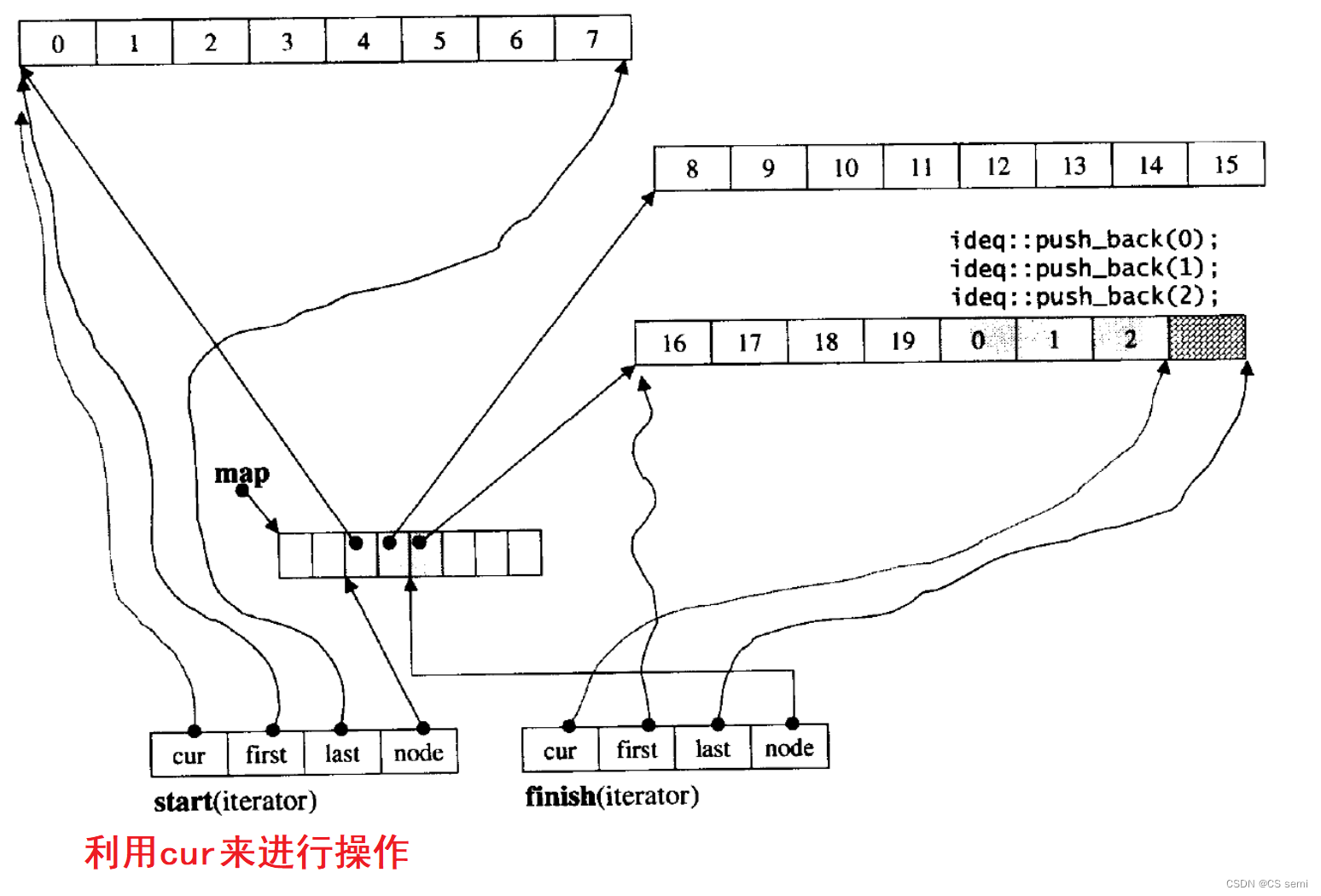
(5)deque缺陷
deque有一个致命缺陷:不适合遍历,因为在遍历时,deque的迭代器要频繁的去检测其是否移动到某段小空间的边界,导致效率低下,而序列式场景中,可能需要经常遍历,因此在实际中,需要线性结构时,大多数情况下优先考虑vector和list,deque的应用并不多,而目前能看到的一个应用就是,STL用其作为stack和queue的底层数据结构
(6)为什么选择deque作为stack和queue的底层默认容器
stack是一种后进先出的特殊线性数据结构,因此只要具有push_back()和pop_back()操作的线性结构,都可以作为stack的底层容器,比如vector和list都可以;queue是先进先出的特殊线性数据结构,只要具有push_back和pop_front操作的线性结构,都可以作为queue的底层容器,比如list。但是STL中对stack和queue默认选择deque作为其底层容器,主要是因为:
- stack和queue不需要遍历(因此stack和queue没有迭代器),只需要在固定的一端或者两端进行操作。
- 在stack中元素增长时,deque比vector的效率高(扩容时不需要搬移大量数据);queue中的元素增长时,deque不仅效率高,而且内存使用率高。结合了deque的优点,而完美的避开了其缺陷。