第四章 数组、串、广义表
一、数组
1.概念:线性表是通过数组实现的,数组是线性表的推广,数组只有存取元素和修改元素的操作(除了初始化和销毁);
2.数组的存储结构:一个数组的所有元素在内存中占用一段连续的存储空间(顺序存储);
- 以行为主顺序优先存储;
- 以列为主顺序优先存储。
3.矩阵的压缩存储(节约空间)
- 对称矩阵:元素关于主对角线对称,利于节约空间,n*(n+1)/2;

- 三角矩阵:上三角或者下三角均为同一个常量,n*(n+1)/2+1;

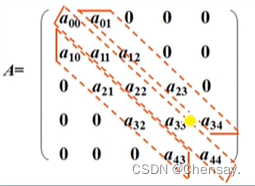
- 三对角矩阵:第一行和最后一行有2非0数字,其余都是3个非0数字,3n-2;转化为一维数组的话,下标是k=2i+j-1(i是这个元素的纵坐标,j是横坐标);
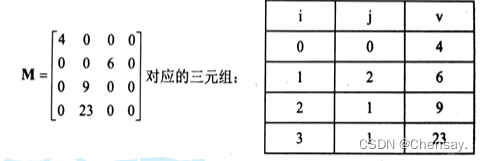
- 稀疏矩阵:三元组(i,j,v)记录了非零元素的行号i、列号j以及非零的元素v(一般压缩存储方法有三元组顺序表和十字链表);
二、串
1.概念:特殊的线性表,数据元素是仅是一个字符组成,所以串是由0个或多个字符组成的有限序列;无元素叫空串(空格串不是空串),包含子串的叫主串,默认以1开头;
2.基本存储方式:顺序存储和链式存储;
3.子串:串中任意连续字符组成的子序列,空串是任意串的子串,任意串是其自身的子串;
- 长度为n的字符串的子串个数:
- 有n(n+1)/2 +1个子串;
- 非空子串:n(n+1)/2;
- 非空真子串:n(n+1)/2-1。
4.串相等:两串串值相等(相同),但两串长度相等时,各个对应位置的字符都相等才相等;
5.串的模式匹配算法:简单说就是在文本中查找某字符;
- 简单匹配:时间复杂度O(n*m),n和m分别是主串和模式串(子串)的长度;
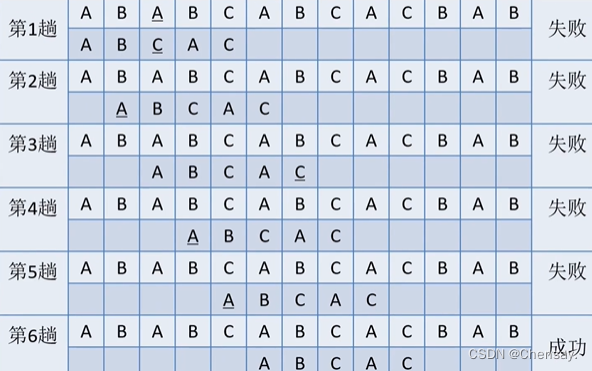
- KMP算法:相对比较方便
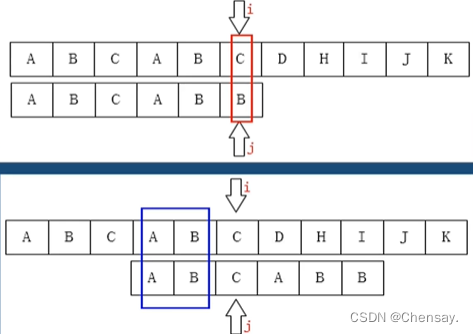
- 前缀:第一个字母开头,不包括全部;如:absd,前缀是a、ab、ads;
- 后缀:最后一个字母开头,不包括全部;如:absd,后缀是d、sd、bsd;
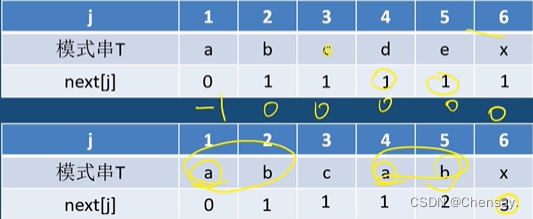
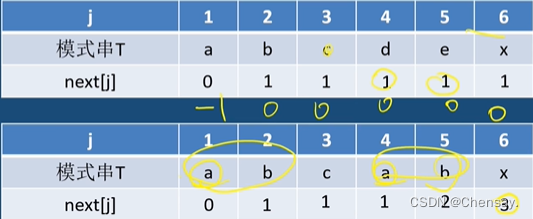
- 求next:next[1]=0,前后缀重合时加1,否则就是1;
三、广义表
1.概念:简称表,一种递归的数据结构,通常使用链式存储结构;时线性表的推广,由于有两种数据元素,所以需要两种结构的结点,表结点和原子结点;
2.特征:
- 广度:定义最外层包含的元素个数,把最外层的括号去掉就很明显了;
- 深度:定义所含弧的重数;原子深度为0,空表为1;
- 任何一个非空广义表GL可分解为表头head(GL)=al和表尾tail(GL)=(a2,…,an)两部分;
- 小写字母表示原子,大写字母表示广义表表名;
- 例子:A=()
B=(e)
C=(a,(bcd))
D=(A,B,C)=((),(e),(a,(b,cd)) E=((a,(a,b),((a,b),c)))
A是一个空表,其长度为0,其深度为1;
B是只含有单个原子e的表,其长度为1其深度为1:
C有两个元素,一个是原子a,另一个是子表,其长度为2,其深度为2;
D有三个元素,每个元素都是一个表,其长度为3,其深度为3;
E中只含有一个元素,是一个表,它的长度为1,其深度为4; - 表结点的三个域:标志域、指示表头的指针的指针域、指示表尾的指针的指针域,tag=1;
- 原子域:两个域,标志域和值域,tag=0;

3.广义表中的head和tail的运算 - 表头:表中第一个元素,可以是原子、子表;
- 表尾:必定时子表
- 操作:取出
- 例题:已知广义表LS=((a,b,c),(d,e,f)),取出e,使用tail和head如何取出来?tail(LS)=((d,e,f))
head(tail(LS))=(def) tail(head(tail(LS)))=(e,f) //无论如何都会加上这个()括号
head(tail(head(tail(Ls)))=e //head可以去除单个元素
- 例题:已知广义表LS=((a,b,c),(d,e,f)),取出e,使用tail和head如何取出来?tail(LS)=((d,e,f))







![[算法通关村] 1.1 单向链表的创建](https://img-blog.csdnimg.cn/c81d3edf4b8e4e7ba6f6b25eca94e768.png)