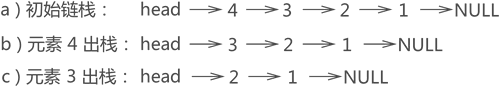一.队列的基本概念
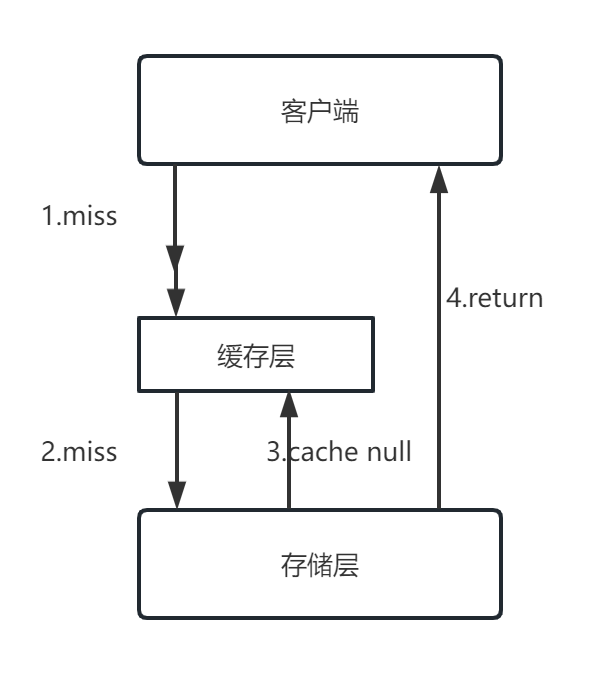
队列是另一种特殊的表,这种表只在表首(也称为队首)进行删除操作,只在表尾进行插入操作。队列的修改是按先进先出的规则进行的,所以队列又称为先进先出表,First In First Out,简称FIFO表。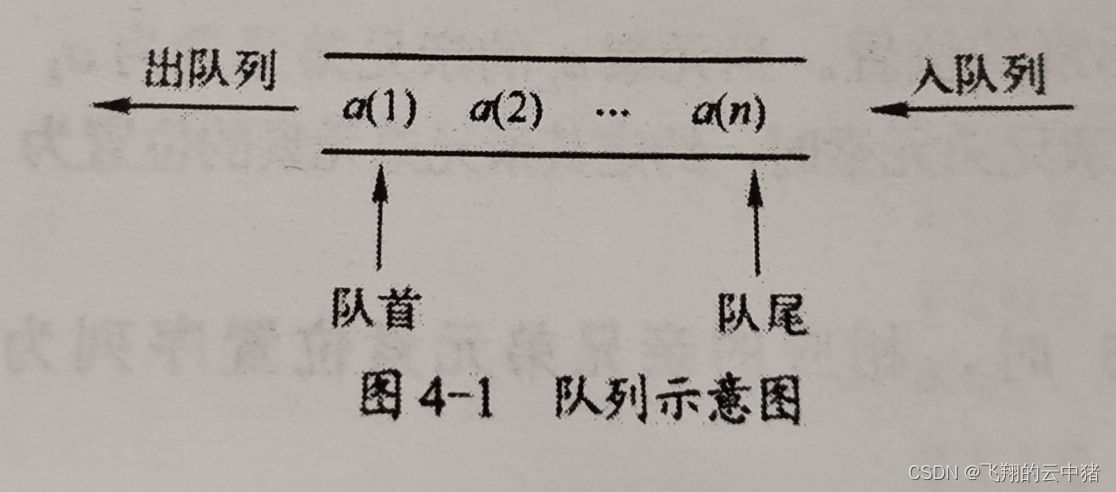
如示意图所示,a(1)就是队首元素,a(n)就是队尾元素。队列中的元素是按顺序进入的,退出队列也只能按照这个次序一次退出。
二.队列的基本运算
1.QueueEmpty(Q):测试队列Q是否为空
2.QueueFull(Q):测试队列Q是否已满
3.QueueFirst(Q):返回队列Q的队首元素
4.QueueLast(Q):返回队列Q的队尾元素
5.EnterQueue(x,Q):在队列的Q的队尾插入元素x
6.DeleteQueue(Q):闪出并返回队列Q的队首元素
三.队列的实现
1.用指针实现队列
因为队列也是一种特殊的表,所以实现与表类似,只不过要实现的基本运算不一样。
2.用循环数组实现队列
四.队列的应用
例一:电路布线问题【广度搜索算法】
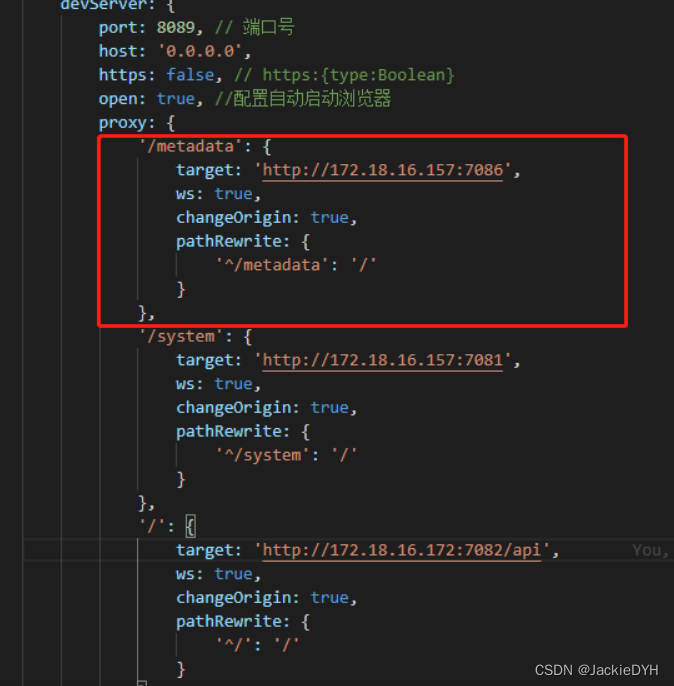
印制电路板将布线区域划分成n*m个方格,如图所示。
精确的电路布线问题要求确定连接方格a的中点到方格b的中点的最短布线方案。在布线时,电路只能沿之心啊或直角布线,如图b所示。为了避免线路相交,已布了线的方格做了封锁标记,其他线路不允许穿过被封锁的方格。
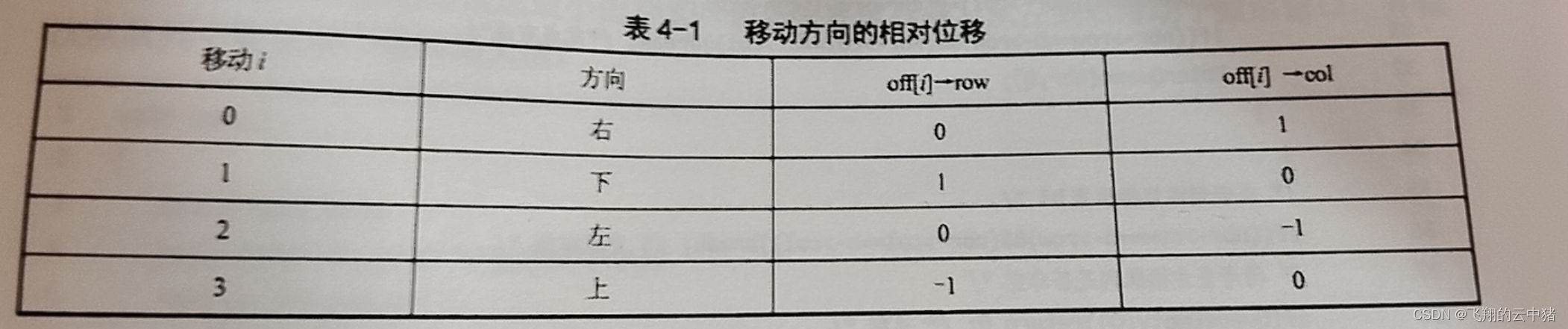
下面讨论队列在电路布线问题中的应用。解电路布线问题,首先从起始位置a开始,将它作为第1个考察方格。与该考察方格相邻并且可达的方格成为待考察方格,加入到带考察方格队列中,并标记为1,即从其实方格a到这些方格的距离为1。然后,算法从带考察方格队列中取出队首结点,作为下一个考查方格,并将与当前考查方格相邻且为标记过的方格标记为2,存入代考察方格队列。这个过程一直继续到算法搜索到目标方格b或代考察方格队列为空时止。
在实现上述算法之前,首先定义一个表示电路板上下方格位置的结构Pos,它的两个成员row和col分别表示方格所在的行和列。
typedef struct pnode *Pos;//位置结点指针类型
struct pnode{//位置结点
int row,//行
col;//列
}Pnode;
此时队列元素的类型是Pos,因此队列元素QItem定义如下。
typedef Pos QItem;//队列元素类型
typedef QItem* Qaddr;//队列元素指针类型
Pos NewPos(){
return (Pos)malloc(sizeof(Pnode));
}
void QItemShow(QItem x){
printf("%d %d\n",x->row,x->col);
}
在实现上述算法是,用一个二维数组g表示所给的方格列阵。初始是,g[i][j]=0,表示该方格允许布线;而g[i][j]=1表示该方格被封锁,不允许布线。为便于处理方格边界的情况,算法在所给方格阵列四周设置一道“围墙”,即增设标记为“1”的附加方格。算法爱是是测试初始方格与目标方格是否相同。若这两个翻个相同则不必计算,直接返回最短距离0,否则算法设置方格阵列的围墙,初始化位移矩阵off。算法将起始位置的距离标记为2。由于数字0和1用于表示方格的开放或封锁状态,所以在表示距离时不用这两个数字,而将距离的值都加2。实际距离应为标记距离减2。算法从起始位置a开始,标记所有标记距离为3的方格并存入考察队列,然后一次标记所有标记距离为4,5...的方格,直至到达目标方格b或待考察方格队列为空。