文章目录
- 6889.特殊元素平方和
- 思路
- 完整版
- 取模注意:不能对0取余/取模
- 解答错误:本题的数组最后一个下标是nums[nums.size()]
- 6929.数组的最大美丽值(排序+滑动窗口)
- 思路1:排序+滑动窗口
- 注意点
- 6927. 合法分割的最小下标(倒推的思路)
- 思路
- 思路1:哈希表统计元素频率
- 思路2:投票法找出出现频率最高的元素
- 投票法介绍
- 补充:投票法
6889.特殊元素平方和
- 主要注意点是本题的
i并不是数组下标的i,是按照数字顺序来的
给你一个下标从 1 开始、长度为 n 的整数数组 nums 。
对 nums 中的元素 nums[i] 而言,如果 n 能够被 i 整除,即 n % i == 0 ,则认为 num[i] 是一个 特殊元素 。
返回 nums 中所有 特殊元素 的 平方和 。
示例 1:
输入:nums = [1,2,3,4]
输出:21
解释:nums 中共有 3 个特殊元素:nums[1] ,因为 4 被 1 整除;nums[2] ,因为 4 被 2 整除;以及 nums[4] ,因为 4 被 4 整除。
因此,nums 中所有元素的平方和等于 nums[1] * nums[1] + nums[2] * nums[2] + nums[4] * nums[4] = 1 * 1 + 2 * 2 + 4 * 4 = 21 。
示例 2:
输入:nums = [2,7,1,19,18,3]
输出:63
解释:nums 中共有 4 个特殊元素:nums[1] ,因为 6 被 1 整除;nums[2] ,因为 6 被 2 整除;nums[3] ,因为 6 被 3 整除;以及 nums[6] ,因为 6 被 6 整除。
因此,nums 中所有元素的平方和等于 nums[1] * nums[1] + nums[2] * nums[2] + nums[3] * nums[3] + nums[6] * nums[6] = 2 * 2 + 7 * 7 + 1 * 1 + 3 * 3 = 63 。
提示:
- 1 <=
nums.length== n <= 50 - 1 <=
nums[i]<= 50
思路
本题属于比较简单的模拟题,遍历再模拟是否整除即可。
完整版
class Solution {
public:
int sumOfSquares(vector<int>& nums) {
int sum=0;
int n=nums.size();//本题的判断对象是n
//for循环遍历里面是本题的自定义数组下标
for(int i=1;i<=nums.size();i++){
if(n%i==0){
//此处是真实的数组下标
sum+=nums[i-1]*nums[i-1];
}
}
return sum;
}
};
取模注意:不能对0取余/取模
因为数组的下标从0开始,但是所有对0的取余/取模运算都是违法的。
最开始写成了:
class Solution {
public:
int sumOfSquares(vector<int>& nums) {
int sum=0;
int n=nums.size();//本题的判断对象是n
for(int i=0;i<nums.size();i++){
if(n%i==0){
sum+=nums[i]*nums[i];
}
}
return sum;
}
};
但是会出现执行错误,不能对0取模

解答错误:本题的数组最后一个下标是nums[nums.size()]
当我们直接改成初始值i=1,又会出现结果错误
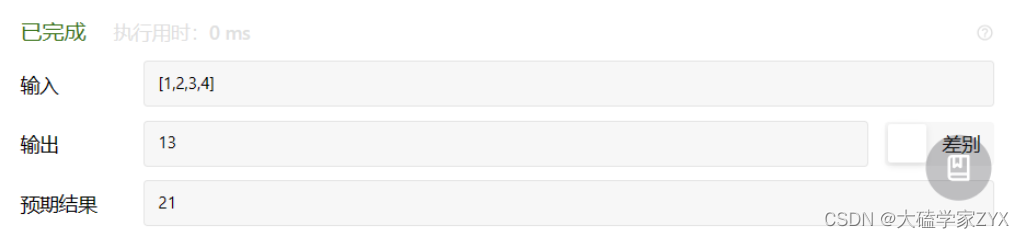
原因是从示例中我们看出,nums[4]是最后一个元素,也就是说本题的下标并不是按照普通数组的形式,而是与数字顺序一致,题目里的数组下标特殊含义也要注意。

因此,本题的for循环应该从i=1开始遍历,一直到i=nums.size()。内部求平方和的逻辑直接用nums[i-1]进行计算。
6929.数组的最大美丽值(排序+滑动窗口)
- 本题主要是需要想到,经过排序,相等的元素会相邻在一起,也就是说相等的元素成为了连续序列,求序列最大长度就是滑动窗口类型题目了。
- 本题关于元素顺序保持不变的要求可以忽略,一是因为求最大长度和元素顺序无关,二是因为所有解法都不能保证不改变元素顺序。(需要排序)
给你一个下标从 0 开始的整数数组 nums 和一个 非负 整数 k 。
在一步操作中,你可以执行下述指令:
- 在范围
[0, nums.length - 1]中选择一个 此前没有选过 的下标i。 - 将
nums[i]替换为范围[nums[i] - k, nums[i] + k]内的任一整数。
数组的 美丽值 定义为数组中由相等元素组成的最长子序列的长度。
对数组 nums 执行上述操作任意次后,返回数组可能取得的 最大 美丽值。
**注意:**你 只 能对每个下标执行 一次 此操作。
数组的 子序列 定义是:经由原数组删除一些元素(也可能不删除)得到的一个新数组,且在此过程中剩余元素的顺序不发生改变。
示例 1:
输入:nums = [4,6,1,2], k = 2
输出:3
解释:在这个示例中,我们执行下述操作:
- 选择下标 1 ,将其替换为 4(从范围 [4,8] 中选出),此时 nums = [4,4,1,2] 。
- 选择下标 3 ,将其替换为 4(从范围 [0,4] 中选出),此时 nums = [4,4,1,4] 。
执行上述操作后,数组的美丽值是 3(子序列由下标 0 、1 、3 对应的元素组成)。
可以证明 3 是我们可以得到的由相等元素组成的最长子序列长度。
示例 2:
输入:nums = [1,1,1,1], k = 10
输出:4
解释:在这个示例中,我们无需执行任何操作。
数组 nums 的美丽值是 4(整个数组)。
提示:
1 <= nums.length <= 1050 <= nums[i], k <= 105
思路1:排序+滑动窗口
因为美丽值的定义是数组中由相等元素组成的最长子序列的长度,因此我们想要获得全部都是相等元素的序列,并求最大长度。
虽然本题要求 子序列 定义是剩余元素的顺序不发生改变,但是求的是相等元素组成的最长子序列长度,因此元素的顺序并不影响结果。
(实际上本题所有解法都不考虑元素顺序,所以这个条件有点问题)
因此我们可以先进行排序,让相等的元素排在一起,此时只需要判断窗口左端点(最小值)和右端点(最大值)是不是相等,也就是只有nums[r]-k<=nums[l]+k的时候,才作为有效窗口。
此时,本题就转变成了,求满足nums[r]-k<=nums[l]+k条件的最长子序列,也就是找最长的连续子数组,其最大值-最小值不超过2k。
也属于找最长子序列问题。最长子序列需要枚举右端点,只有不满足条件的时候,才更新左端点。
算法专题整理:滑动窗口_大磕学家ZYX的博客-CSDN博客
class Solution {
public:
int maximumBeauty(vector<int>& nums, int k) {
sort(nums.begin(), nums.end());
int res=0;
for (int l = 0, r = 0; r < nums.size(); ++r) {
while (nums[r]-k > nums[l] + k) {
l++;
}
res = max(res, r - l + 1);
}
return res;
}
};
注意点
由于选的是子序列,且子序列的元素都相等,所以元素顺序对答案没有影响,可以先对数组排序。
且仔细看用例1可以看出,并不要求最后的子数组在原数组也是连续的,只是找替换后相等的数字组成的总长度,并不是找原数组中就连续的子数组!
参考题解:
灵茶山艾府
力扣周赛总结
6927. 合法分割的最小下标(倒推的思路)
- 本题重点是想明白,如果想要相等,最后那个结果肯定是原数组的支配元素。
- 因此可以根据支配元素的结果倒推,已知支配元素一定是这个数值,去求那两个子数组支配元素是不是这个。这种倒推的思路要注意。
如果元素 x 在长度为 m 的整数数组 arr 中满足 freq(x) * 2 > m ,那么我们称 x 是 支配元素 。其中 freq(x) 是 x 在数组 arr 中出现的次数。注意,根据这个定义,数组 arr 最多 只会有 一个 支配元素。
给你一个下标从 0 开始长度为 n 的整数数组 nums ,数据保证它含有一个支配元素。
你需要在下标 i 处将 nums 分割成两个数组 nums[0, ..., i] 和 nums[i + 1, ..., n - 1] ,如果一个分割满足以下条件,我们称它是 合法 的:
0 <= i < n - 1nums[0, ..., i]和nums[i + 1, ..., n - 1]的支配元素相同。
这里, nums[i, ..., j] 表示 nums 的一个子数组,它开始于下标 i ,结束于下标 j ,两个端点都包含在子数组内。特别地,如果 j < i ,那么 nums[i, ..., j] 表示一个空数组。
请你返回一个 合法分割 的 最小 下标。如果合法分割不存在,返回 -1 。
示例 1:
输入:nums = [1,2,2,2]
输出:2
解释:我们将数组在下标 2 处分割,得到 [1,2,2] 和 [2] 。
数组 [1,2,2] 中,元素 2 是支配元素,因为它在数组中出现了 2 次,且 2 * 2 > 3 。
数组 [2] 中,元素 2 是支配元素,因为它在数组中出现了 1 次,且 1 * 2 > 1 。
两个数组 [1,2,2] 和 [2] 都有与 nums 一样的支配元素,所以这是一个合法分割。
下标 2 是合法分割中的最小下标。
示例 2:
输入:nums = [2,1,3,1,1,1,7,1,2,1]
输出:4
解释:我们将数组在下标 4 处分割,得到 [2,1,3,1,1] 和 [1,7,1,2,1] 。
数组 [2,1,3,1,1] 中,元素 1 是支配元素,因为它在数组中出现了 3 次,且 3 * 2 > 5 。
数组 [1,7,1,2,1] 中,元素 1 是支配元素,因为它在数组中出现了 3 次,且 3 * 2 > 5 。
两个数组 [2,1,3,1,1] 和 [1,7,1,2,1] 都有与 nums 一样的支配元素,所以这是一个合法分割。
下标 4 是所有合法分割中的最小下标。
示例 3:
输入:nums = [3,3,3,3,7,2,2]
输出:-1
解释:没有合法分割。
提示:
1 <= nums.length <= 1051 <=nums[i] <= 109nums有且只有一个支配元素。
思路
这道题的重要注意点在于,如果想要两个子数组的支配元素相等,那么这个支配元素,肯定也是原数组的支配元素!
所以就可以倒过来推导,先求原数组支配元素,然后再看这个支配元素,是否在两个子数组里也是支配的!
想明白这一点之后,剩下的就是模拟了,模拟的部分也可以练习一下。
思路1:哈希表统计元素频率
首先,要找到这个数组的支配元素。我们可以使用哈希表(unordered_map)来存储每个元素的频率。在这个过程中,我们同时找出频率最高的元素,即为我们的支配元素。
在找到支配元素后,再次遍历数组。这一次遍历要找出合法的分割点。一个合法的分割点需要满足以下条件:
- [0, …, i] 的支配元素与整个数组的支配元素相同,即 nums[i] == dominator;
- 在当前分割点之前(包括分割点),支配元素的出现次数超过了数组的一半,即 count > (i + 1) / 2;
- 在当前分割点之后,剩余的支配元素出现次数仍超过后半部分数组的一半,即 (maxFreq - count) > (n - i - 1) / 2。
- 如果当前分割点满足以上所有条件,我们就找到了一个合法的分割点。我们需要找的是最小的分割点,所以一旦找到,我们就直接返回这个分割点的索引 i。
class Solution {
public:
int minimumIndex(vector<int>& nums) {
//先建立哈希表统计原数组的支配元素
unordered_map<int,int>umap;
//遍历所有元素统计频率
int maxFreq = 0;
int x=0;
for(int i=0;i<nums.size();i++){
umap[nums[i]]++;
//最大频率
if(umap[nums[i]]>maxFreq){
maxFreq = umap[nums[i]];
x=nums[i];//同时存储频率最高数值
}
}
//遍历i,对于i分割的两个子数组判断支配元素是不是x
int count=0;
for(int i=0;i<nums.size();i++){
if(nums[i]==x){ //统计支配元素的频率
count++;
}
//统计完了可以直接判断i之前元素的count是不是>长度/2,之后的频率是不是>长度/2
//注意边界条件的长度,i+1已经算了i本身了,后面的nums.size()-i就不能算i了!
if(count>(i+1)/2&&(maxFreq-count)>(nums.size()-i-1)/2){
return i;
}
}
return -1;
}
};
思路2:投票法找出出现频率最高的元素
也可以用投票法,求出占比最高的元素及其频率。
投票法介绍
投票法是一种用于找出数组中多数元素的算法,这个算法的基本原理是:
如果一个元素是数组的多数元素(出现次数超过数组长度的一半),那么即使我们把它和其他每个不同的元素一一抵消(每次都从数组中删除两个不同的元素),最后剩下的一定是这个多数元素。
由于题目保证了数组中最多只存在一个支配元素,投票法最后找到的元素必然是这个支配元素。
class Solution {
public:
int minimumIndex(vector<int>& nums) {
int n = nums.size();
int cnt = 0, x = 0;
// 投票法求元素 x
for (int num: nums) { // 遍历数组
if (num == x) { // 如果当前元素等于候选元素
cnt++; // 候选元素的票数加一
} else { // 如果当前元素不等于候选元素
cnt--; // 候选元素的票数减一,相当于抵消掉了
if (cnt < 0) { // 如果票数小于0
x = num; // 将当前元素作为新的候选元素
cnt = 1; // 将新的候选元素的票数设为1
}
}
}
// 求 x 出现的总数
int sum = 0;
for (int num: nums) { // 再次遍历数组
if (x == num) sum++; // 如果当前元素等于支配元素,将支配元素的总数加一
}
// 枚举求解 i
cnt = 0;
for (int i = 0; i < n; ++i) { // 再次遍历数组,寻找分割点
if (x == nums[i]) cnt++; // 如果当前元素等于支配元素,将支配元素的出现次数加一
if (cnt * 2 > (i + 1) && (sum - cnt) * 2 > (n - i - 1))
return i; // 检查是否满足分割条件,如果满足,返回当前索引
}
return -1; // 如果遍历完数组都没有找到合法的分割点,返回-1
}
};
补充:投票法
- 投票法是找**数组中出现频率超过半数(必须是超过不能是等于)**的元素。
- 数组中出现频率超过半数的元素,一定只有一个!
投票法(Boyer-Moore Voting Algorithm)是一种用于在数组中查找主要元素的算法,主要元素定义为一个元素出现次数超过数组长度的一半。它并不一定能找到频率最高的元素,例如在数组 [1, 2, 2, 3, 3, 3] 中,频率最高的元素是 3,但没有元素出现次数超过数组长度的一半,因此投票法不会返回任何元素。如果数组 [1, 1, 2, 2, 3, 3, 3, 3] 中,频率最高的元素也是主要元素,这时投票法会返回元素 3。
示例:
class Solution {
public:
int majorityElement(vector<int>& nums) {
int count = 0;
int candidate = 0;
for(int num : nums){
if (count == 0) {
candidate = num; // 当前候选主要元素
}
count += (num == candidate) ? 1 : -1; // 如果当前元素等于候选主要元素,票数加1,否则减1
}
return candidate; // 返回最后的候选主要元素
}
};