最多变的混合模式-实色混合HardMix
之前写过一篇介绍27种图层混合模式的非常详细,如果你想完全了解底层的原理,这篇文章不会让你失望。
PS图层混合模式超详细解答-图层混合模式的原理 - 王先生的副业的文章 - 知乎
https://zhuanlan.zhihu.com/p/643960643
但是在写作的过程中,我发现,27中混合模式,最强大的,反而是最不起眼的实色混合
因为它蕴含着另外一种混合模式(线性光)
通过调整fill也就是填充,我们可以获得不同程度的线性光
公式
r = H a r d M i x ( b , a ) = { 1 b + a ≥ 1 0 e l s e r=HardMix(b,a)=\left\{ \begin{aligned}&1&b+a\geq 1\\&0&else \end{aligned}\right. r=HardMix(b,a)={10b+a≥1else
由公式我们可以看出,最后的结果只有两个,所以最后之后保留 2 3 = 8 2^3=8 23=8种颜色,也就是
( 0 , 0 , 0 ) 黑 ( 1 , 0 , 0 ) 红 ( 1 , 1 , 0 ) 黄 ( 1 , 1 , 1 ) 白 ( 0 , 1 , 0 ) 绿 ( 0 , 1 , 1 ) 青 ( 1 , 0 , 1 ) 品红 ( 0 , 0 , 1 ) 蓝 \begin{aligned}(0,0,0)&黑\\(1,0,0)&红\\(1,1,0)&黄\\(1,1,1)&白\\(0,1,0)&绿\\(0,1,1)&青\\(1,0,1)&品红\\(0,0,1)&蓝\end{aligned} (0,0,0)(1,0,0)(1,1,0)(1,1,1)(0,1,0)(0,1,1)(1,0,1)(0,0,1)黑红黄白绿青品红蓝
加上fill
但是如果填充介入表达式,则结果将合线性光类似
r
=
H
a
r
d
M
i
x
f
i
l
l
(
b
,
a
)
=
{
0
f
i
l
l
×
a
+
b
−
f
i
l
l
(
1
−
f
i
l
l
)
<
0
f
i
l
l
×
a
+
b
−
f
i
l
l
(
1
−
f
i
l
l
)
0
≤
f
i
l
l
×
a
+
b
−
f
i
l
l
(
1
−
f
i
l
l
)
≤
1
1
f
i
l
l
×
a
+
b
−
f
i
l
l
(
1
−
f
i
l
l
)
>
1
r=HardMix_{fill}(b,a)=\left\{ \begin{aligned}&0& \frac{fill\times a+b-fill}{(1-fill)}<0\\ &\\ &\frac{fill\times a+b-fill}{(1-fill)}&0\leq \frac{fill\times a+b-fill}{(1-fill)}\leq 1\\&\\ &1& \frac{fill\times a+b-fill}{(1-fill)}>1 \end{aligned}\right.
r=HardMixfill(b,a)=⎩
⎨
⎧0(1−fill)fill×a+b−fill1(1−fill)fill×a+b−fill<00≤(1−fill)fill×a+b−fill≤1(1−fill)fill×a+b−fill>1
如果fill的取值是
0.5
0.5
0.5则
r
=
H
a
r
d
M
i
x
f
i
l
l
(
b
,
a
)
=
{
0
0.5
×
a
+
b
−
0.5
(
1
−
0.5
)
<
0
0.5
×
a
+
b
−
0.5
(
1
−
0.5
)
0
≤
0.5
×
a
+
b
−
0.5
(
1
−
0.5
)
≤
1
1
0.5
×
a
+
b
−
0.5
(
1
−
0.5
)
>
1
=
{
0
a
+
2
b
−
1
<
0
a
+
2
b
−
1
0
≤
a
+
2
b
−
1
≤
1
1
a
+
2
b
−
1
>
1
\begin{aligned}r=HardMix_{fill}(b,a)=&\left\{ \begin{aligned}&0& \frac{0.5\times a+b-0.5}{(1-0.5)}<0\\ &\\ &\frac{0.5\times a+b-0.5}{(1-0.5)}&0\leq \frac{0.5\times a+b-0.5}{(1-0.5)}\leq 1\\ &\\&1& \frac{0.5\times a+b-0.5}{(1-0.5)}>1 \end{aligned}\right.\\&\\&=\left\{ \begin{aligned}&0& a+2b-1<0\\ &\\ &a+2b-1&0\leq a+2b-1\leq 1\\&\\ &1& a+2b-1>1 \end{aligned}\right.\end{aligned}
r=HardMixfill(b,a)=⎩
⎨
⎧0(1−0.5)0.5×a+b−0.51(1−0.5)0.5×a+b−0.5<00≤(1−0.5)0.5×a+b−0.5≤1(1−0.5)0.5×a+b−0.5>1=⎩
⎨
⎧0a+2b−11a+2b−1<00≤a+2b−1≤1a+2b−1>1
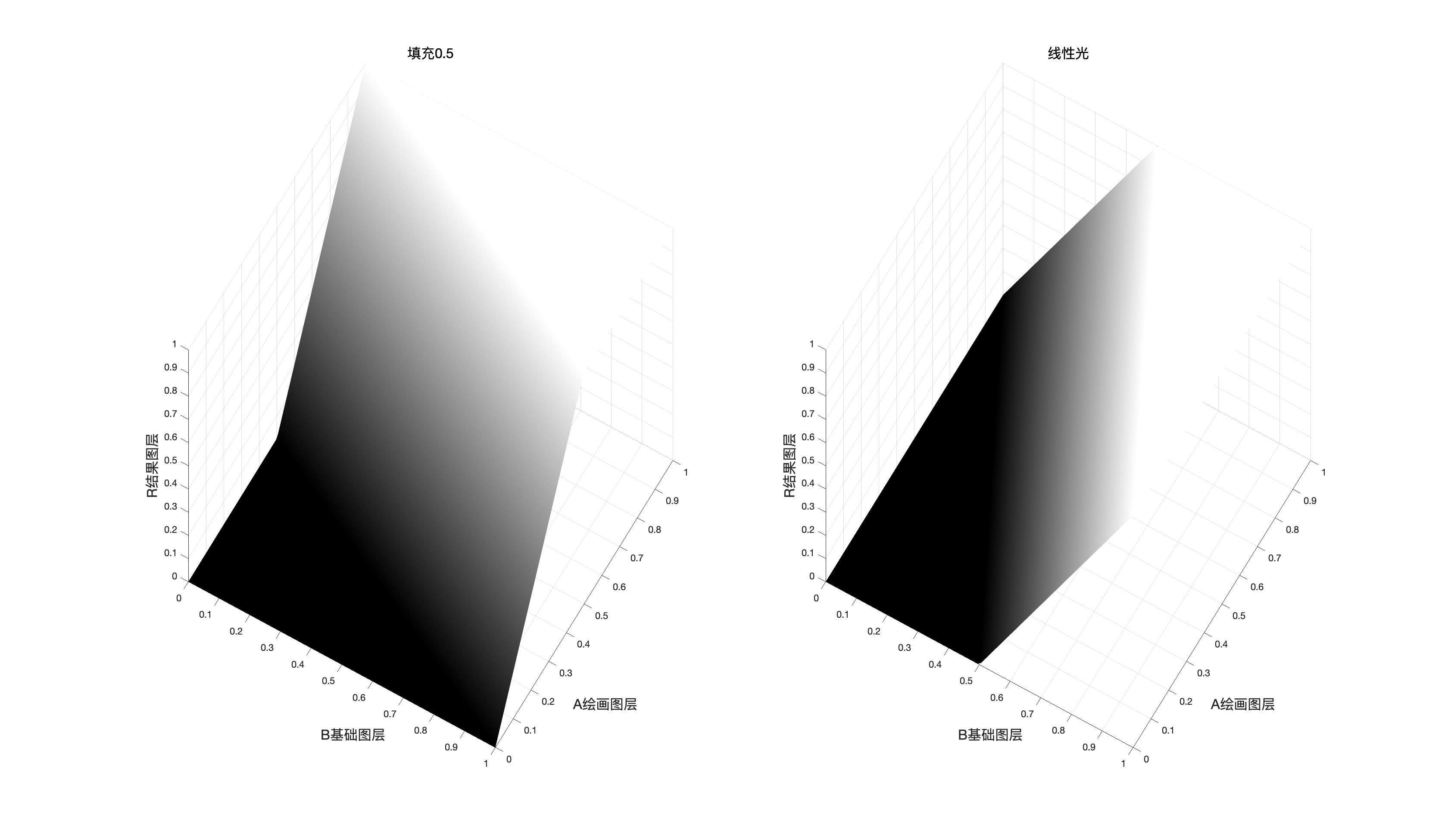
上面的结果就是线性光的表达式,也就是说此时二者等价,或者说是互逆,也就是说,实色混合其实是线性光的强化版本,可以实现线性光的功能而去变化更多。
为了让我们更加直观得看到,为什么实色混合可以变身成线性光,我们把fill也就是填充的值,从
0.2
→
0.9
0.2→0.9
0.2→0.9都在matlab中画出来。直观上,就像是一本桌子上的书逐渐被扶正的过程。
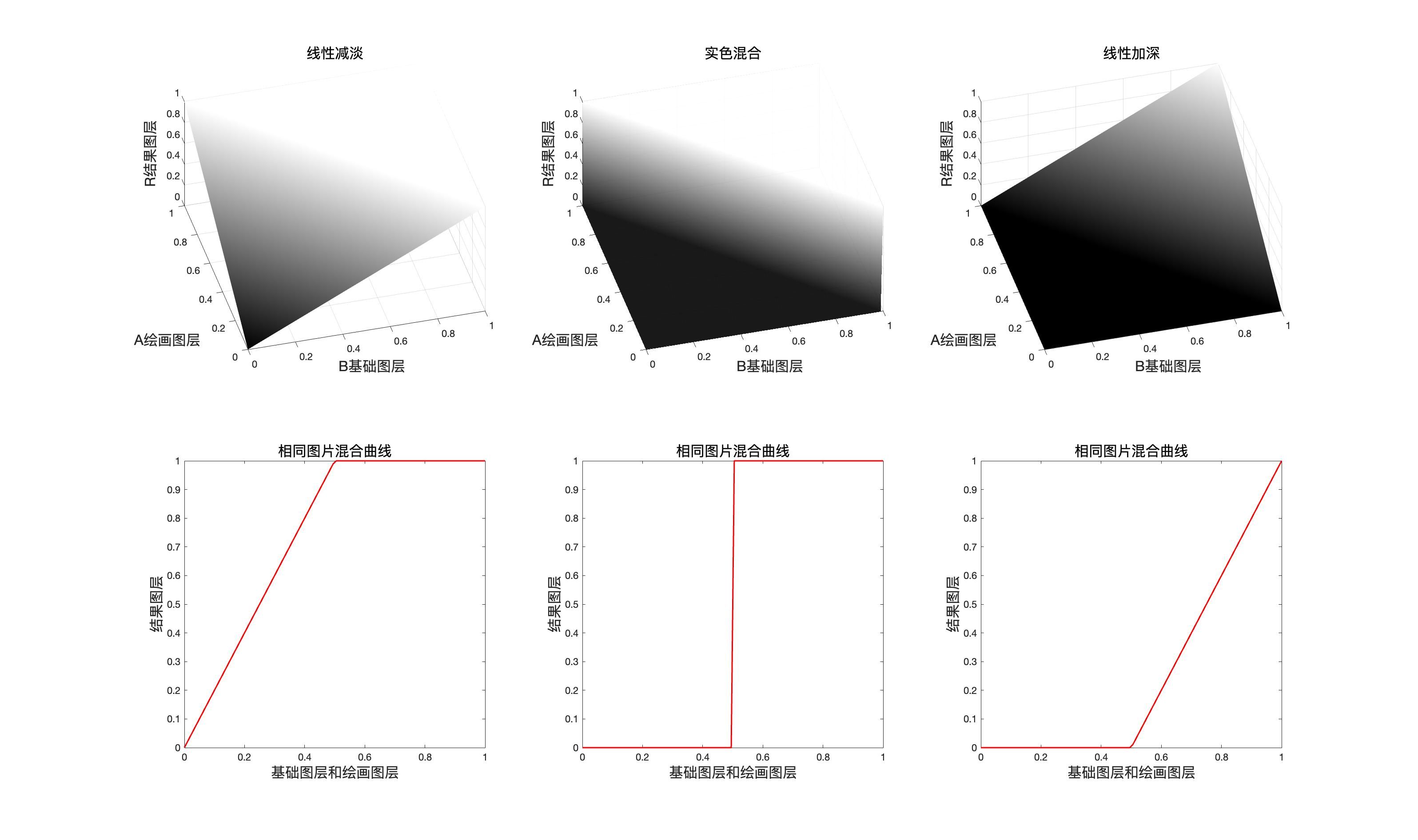
如果我们按照刚才的包含fill的公式在matlab中绘制映射面,那么我们可以得到不同款式的线性光
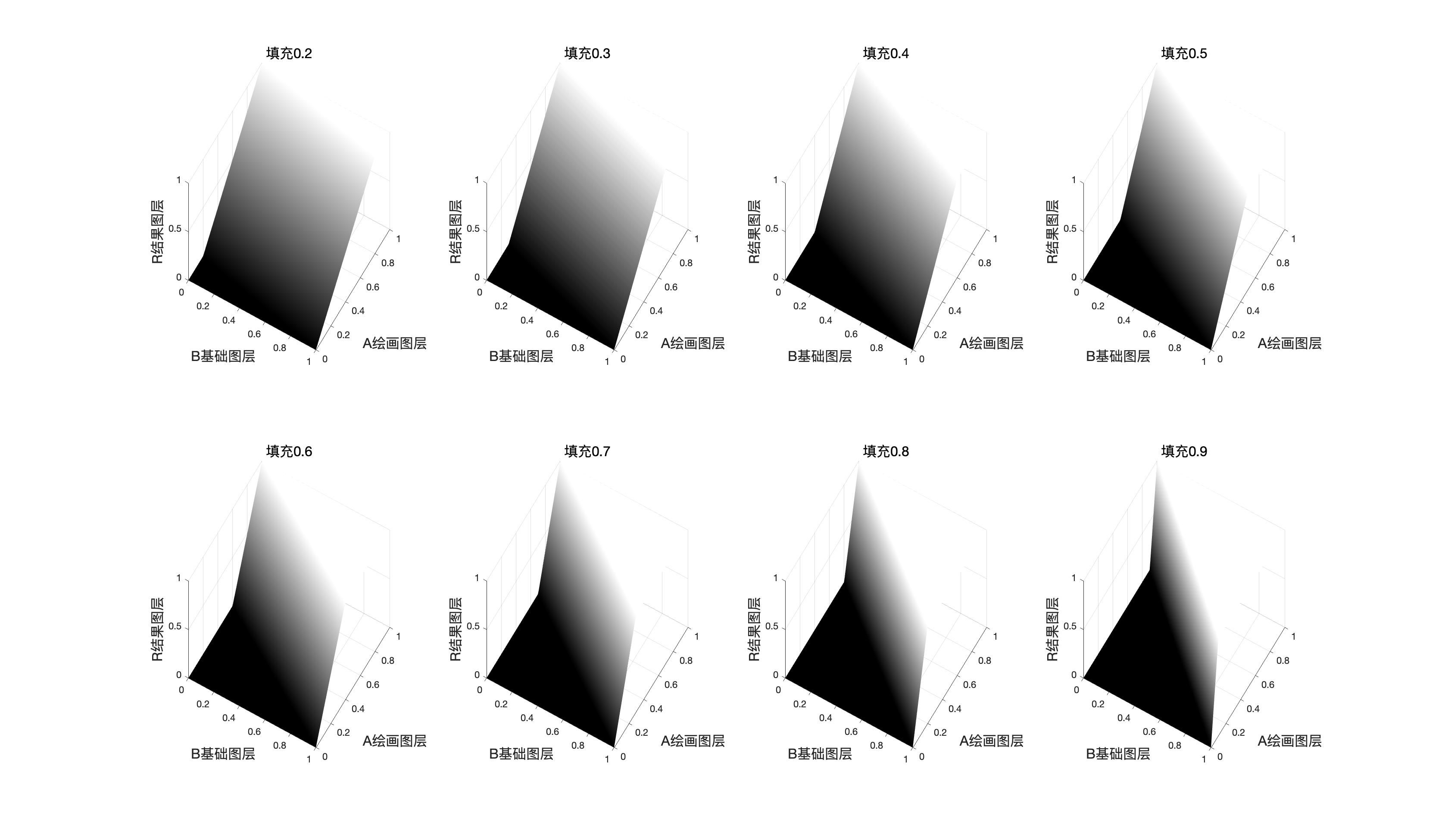
如果我们把线性光的映射面和实色混合的对比,那么我们可以看到,这两个图像是对称的,换句话说,只要把图层顺序修改,那么两者等价。