144. 二叉树的前序遍历
文章目录
- [144. 二叉树的前序遍历](https://leetcode.cn/problems/binary-tree-preorder-traversal/)
- 一、题目
- 二、思路及代码
- (1)递归
- (2)迭代(两种方法)
一、题目
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
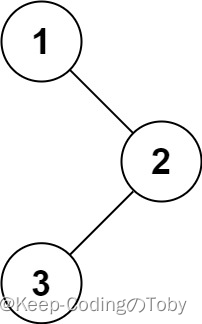
输入:root = [1,null,2,3]
输出:[1,2,3]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
示例 4:
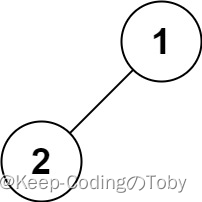
输入:root = [1,2]
输出:[1,2]
示例 5:
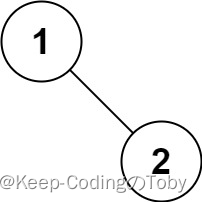
输入:root = [1,null,2]
输出:[1,2]
提示:
- 树中节点数目在范围
[0, 100]内 -100 <= Node.val <= 100
**进阶:**递归算法很简单,你可以通过迭代算法完成吗?
二、思路及代码
(1)递归
算法思路:
这道题目要求实现二叉树的前序遍历,前序遍历的顺序是根节点、左子树、右子树。这里采用递归的方法实现前序遍历。
具体思路:
- 定义一个递归函数,传入根节点和结果向量
- 如果根节点为空,直接返回
- 如果根节点不为空,则先将根节点值加入结果向量
- 递归调用左子树,实现左子树的前序遍历
- 递归调用右子树,实现右子树的前序遍历
- 最终结果向量即为前序遍历结果
具体实现:
- 定义preorder递归函数,传入根节点和结果向量
- 判断根节点是否为空,为空直接返回
- 不为空则将根节点值加入结果向量vec
- 递归preorder左子树
- 递归preorder右子树
- 主函数中调用preorder后返回vec即为结果
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void preorder(TreeNode*root, vector<int> &vec){
if(root == NULL){
return;
}
vec.push_back(root->val);
preorder(root->left,vec);
preorder(root->right,vec);
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result;
preorder(root,result);
return result;
}
};
算法分析:
- 时间复杂度:O(n),需要遍历整个二叉树的所有节点
- 空间复杂度:最坏O(n),递归时栈的深度最多为树的高度
(2)迭代(两种方法)
版本1(更推荐)
算法思路:这道题的目标是实现二叉树的前序遍历,即遍历顺序为根节点、左子树、右子树。前序遍历可以利用栈的先入后出特性实现。
具体思路:
-
定义一个栈和结果数组
-
将根节点入栈
-
当栈不空时,重复以下过程:
3.1 从栈顶取出一个节点,将该节点的值放入结果数组
3.2 先把右子节点入栈(先右后左是为了左子节点先被取出)
3.3 再把左子节点入栈
-
直到栈为空,遍历结束,返回结果数组
这种方法遵循前序遍历的访问顺序,通过栈保证每次都是取栈顶的节点,正确实现了前序遍历。
具体实现:
-
定义栈st和结果数组result
-
判断根节点是否为空,为空直接返回结果数组
-
不为空则将根节点root入栈
-
通过while循环判断栈是否为空
4.1 从栈顶取出一个节点temp
4.2 将temp的节点值放入结果数组
4.3 弹出栈顶节点
4.4 判断右子节点是否为空,不为空则入栈
4.5 判断左子节点是否为空,不为空则入栈
-
遍历结束后返回结果数组
因此通过栈的先入后出实现了遍历顺序为根、左、右的前序遍历。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if(root == NULL){
return result;
}
st.push(root);
while(!st.empty()){
TreeNode *temp = st.top();
result.push_back(temp->val);
st.pop();
if(temp->right != NULL){
st.push(temp->right);
}
if(temp->left != NULL){
st.push(temp->left);
}
}
return result;
}
};
算法分析:
- 时间复杂度:O(n),其中 n 为二叉树的节点数量。需要遍历完全二叉树的所有节点。
- 空间复杂度:O(n),其中 n 为二叉树的节点数量。栈中的元素数量不会超过树的节点数量。
版本2(思路也比较类似)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
stack<TreeNode*> st;
vector<int> v;
TreeNode *p = root;
while(p||!st.empty()){
//当p不为空的时候,p不断向左下走
if(p){
v.push_back(p->val);
st.push(p);
p=p->left;
}
else{
//当p为空的时候,寻找右兄弟,或者是叔叔结点
p=st.top();
st.pop();
p=p->right;
}
}
return v;
}
};