题目链接

leetcode在线oj题——粉刷房子

题目描述

假如有一排房子，共 n 个，每个房子可以被粉刷成红色、蓝色或者绿色这三种颜色中的一种，你需要粉刷所有的房子并且使其相邻的两个房子颜色不能相同。

当然，因为市场上不同颜色油漆的价格不同，所以房子粉刷成不同颜色的花费成本也是不同的。每个房子粉刷成不同颜色的花费是以一个 n x 3 的正整数矩阵 costs 来表示的。

例如，costs[0][0] 表示第 0 号房子粉刷成红色的成本花费；costs[1][2] 表示第 1 号房子粉刷成绿色的花费，以此类推。

请计算出粉刷完所有房子最少的花费成本。

题目示例

示例1

输入: costs = [[17,2,17],[16,16,5],[14,3,19]]
输出: 10
解释: 将 0 号房子粉刷成蓝色，1 号房子粉刷成绿色，2 号房子粉刷成蓝色。
最少花费: 2 + 5 + 3 = 10。

示例2

输入: costs = [[7,6,2]]
输出: 2

题目提示

costs.length == n
costs[i].length == 3
1 <= n <= 100
1 <= costs[i][j] <= 20

解题思路

由于这道题有三个不同的颜色，而题目中使用cost[i][0]代表第i个房子涂成红色的花费，1代表蓝色，2代表绿色，因此我们的dp数组也可以使用0，1，2分别代表红蓝绿

如果从前往后思考，前面一个房子的颜色不确定，因此不知道后一个房子是什么情况，因此我们可以从后往前思考，确定了第i个房子是红色，考虑涂到当前位置需要多少花销

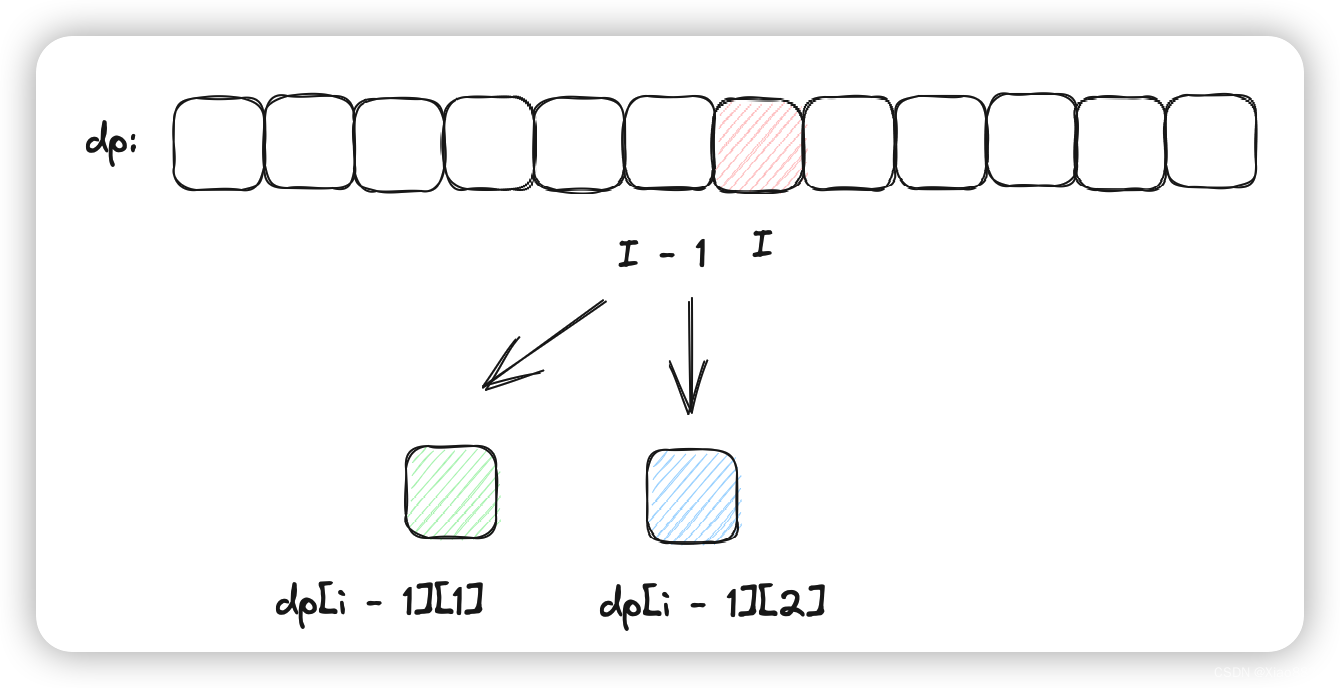
在这里插入图片描述

当第i个房子涂成红色，那么前一个房子只能是蓝色或者绿色，因此涂到当前位置的花费是前一个位置是绿色还是蓝色中的较小值 + 当前位置涂成红色的开销，可以得出涂红色时的状态转移方程：

dp[i][0] = Math.min(dp[i - 1][1], dp[i - 1][2]) + costs[i][0];

其他两种颜色也与之相同

dp[i][1] = Math.min(dp[i - 1][0], dp[i - 1][2]) + costs[i][1];
dp[i][2] = Math.min(dp[i - 1][1], dp[i - 1][0]) + costs[i][2];

最终，直接返回最后一个位置是红蓝绿三种情况中最小花费的即可

完整代码

class Solution {
    public int minCost(int[][] costs) {
        int m = costs.length;
        int n = costs[0].length;
        int[][] dp = new int[m][n];
        //0:red 1:blue 2:green
        dp[0][0] = costs[0][0];
        dp[0][1] = costs[0][1];
        dp[0][2] = costs[0][2];
        for (int i = 1; i < m; i++){
            dp[i][0] = Math.min(dp[i - 1][1], dp[i - 1][2]) + costs[i][0];
            dp[i][1] = Math.min(dp[i - 1][0], dp[i - 1][2]) + costs[i][1];
            dp[i][2] = Math.min(dp[i - 1][1], dp[i - 1][0]) + costs[i][2];
        }
        return Math.min(Math.min(dp[m - 1][0], dp[m - 1][1]), dp[m - 1][2]);
    }
}