1.简述
相关概念介绍
以信号为例,信号在时域下的图形可以显示信号如何随着时间变化,而信号在频域下的图形(一般称为频谱)可以显示信号分布在哪些频率及其比例。频域的表示法除了有各个频率下的大小外,也会有各个频率的相位,利用大小及相位的资讯可以将各频率的弦波给予不同的大小及相位,相加以后可以还原成原始的信号。
时域:描述数学函数或物理信号对时间的关系;例如一个信号的时域波形可以表达信号随着时间的变化[1]。这符合现实世界中人们对信号的认识。
频域:是指在对函数或信号进行分析时,分析其和频率有关部分,而不是和时间有关的部分,和时域一词相对[1]。这不符合现实世界中人们对信号的感官认识,但其为波的形式更符合现实世界中信号的存在,可以辅助人们完成对现实世界中信号的处理,由此产生更多的概率,如频谱、能谱、功率谱、倍频程谱等。
频谱:一个信号是由哪些频率的弦波所组成,也可以看出各频率弦波的大小及相位等信息。一般通过傅里叶变换将时域信号处理成频域信号,获得各个正弦信号的幅度和相位。所得的结果会是分别以幅度及相位为纵轴,频率为横轴的两张图,不过有时也会省略相位的信息,只有不同频率下对应幅度的资料。有时也以“幅度频谱”表示幅度随频率变化的情形,“相位频谱”表示相位随频率变化的情形。
其频谱、能谱、功率谱、倍频程谱的相关概念可看这篇博客:频谱、能谱、功率谱、倍频程谱、1/3 倍频程谱_liyuanbhu的博客-CSDN博客_1/3倍频程
2.代码
%% 正整数的频率表
clear all;
X=[2 3 4 1 2 4 6 5 8 3 2 1 6];
tabulate(X)
%% 样本数据的盒图
clear all;
a=normrnd(1,4,50,1);
b=normrnd(5,1,50,1);
x=[a b];
figure;
boxplot(x,'notch','on','symbol','b*','orientation','vertical');
figure;
boxplot(x,'notch','off','symbol','r+','orientation','horizontal');
3.运行结果
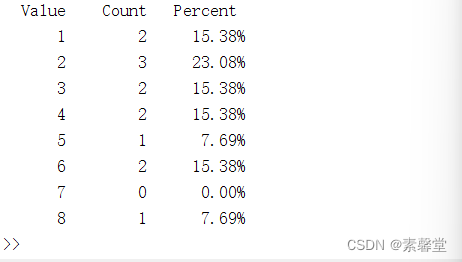
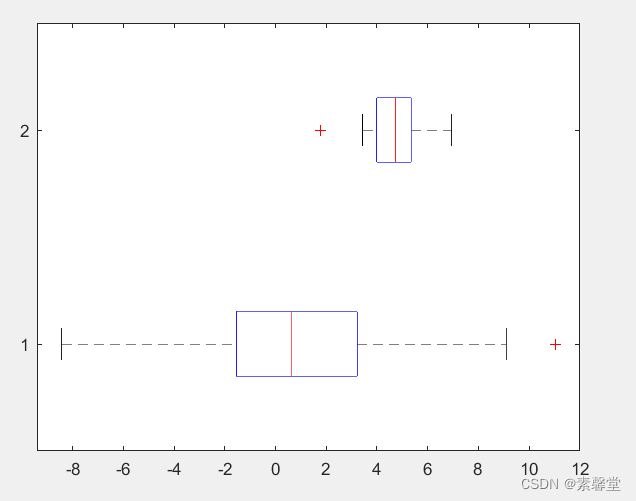
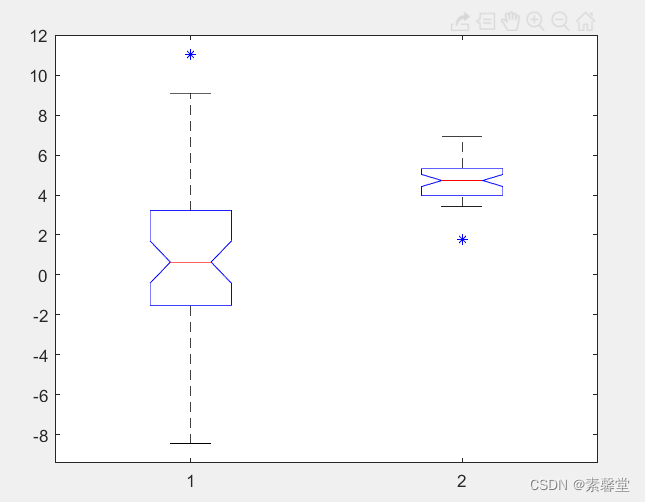


![[Ipsc2009]Let there be rainbows!](https://img-blog.csdnimg.cn/cb22b7e3e06b4ae7a05baed8268499ad.png)