理论参考

【机器学习】EM——期望最大（非常详细）

样例介绍

有c个硬币，每次随机选一个投掷n次，重复执行m次并记录结果。
根据投掷结果计算出每个硬币正面的概率。
每次选择的硬币未知。

过程介绍

随机初始化硬币为正的概率 head_p
根据 head_p 求出选择某个硬币的概率 selected_p
根据 selected_p 计算新的硬币概率 head_p
若 head_p 收敛，执行5；否则，执行2
结束

代码实现

导入库

import random
import numpy as np
from tqdm import tqdm
from collections import Counter
import matplotlib.pyplot as plt

设置硬币朝上的真实值

coin_num：硬币数

coins：硬币正面朝上的真实值

# 设置真实值
coin_num = 5
coins = []
for _ in range(coin_num):
    coins.append(random.randint(0, 100)/100)
coins

模拟投币

随机抽取一个硬币
投掷 n 次
循环 m 次

1 为正面，0 为反面

【注】：在计算概率时并没有乘以组合数，因此当n过大时，概率会精度丢失变为0导致优化失败

0n = 100
m = 1000
coin_result = np.zeros((m, n), dtype=int)

c_selected_record = []
for i_m in range(m):
    # 选择硬币
    coin_p = random.choice(coins)
    c_selected_record.append(coin_p)
    for i_n in range(n):
        # 开始投掷
        coin_result[i_m, i_n] = 1 if random.random() < coin_p else 0

coin_result.shape, Counter(c_selected_record)

EM算法

初始化：随机初始化硬币正面的概率

E步：计算当前硬币的期望
M步：更新硬币参数

为了便于实现，修改概率计算方式，结果不变：

$p^{n_1}\times (1-p)^{n_2} \\ =exp(n_1 \times \log(p) + n_2 \times \log(1-p))$

【注】：预测的硬币并不是一一对应，顺序会变

ini_coin_theta = np.array([random.randint(1, 99)/100 for _ in range(coin_num)])
# coin_theta = np.array([0.2, 0.9])
print('ini coin:', ini_coin_theta)

def E(coin_theta, coin_result):
    
    h_e_sum = np.zeros_like(coin_theta)
    t_e_sum = np.zeros_like(coin_theta)
    
    h_num = coin_result.sum(1)[:, None]
    t_num = coin_result.shape[1] - h_num
    
    # 可以评估每个硬币的得分
    coin_selected_p = h_num @ np.log(coin_theta[None]) + t_num @ np.log(1 - coin_theta[None])
    coin_selected_p = np.exp(coin_selected_p)
    coin_selected_p = coin_selected_p / coin_selected_p.sum(1)[:, None]
    
    h_e = coin_selected_p  * h_num
    t_e = coin_selected_p  * t_num
    
    return h_e.sum(0), t_e.sum(0), coin_selected_p

def M(h_e_sum, t_e_sum):
    return h_e_sum / (h_e_sum + t_e_sum)

max_step=1000
coin_result = np.array(coin_result)

h_e_record = []
t_e_record = []
theta_record = []
delta_record = []

coin_theta = ini_coin_theta
for i in tqdm(range(max_step)):
    h_e_sum, t_e_sum, coin_selected_p = E(coin_theta, coin_result)
    
    h_e_record.append(h_e_sum)
    t_e_record.append(t_e_sum)
    
    new_coin_theta = M(h_e_sum, t_e_sum)
    
    theta_record.append(new_coin_theta)
    
    delta =  ((new_coin_theta - coin_theta)**2).sum()
    
    delta_record.append(delta)
    
    # print(new_coin_theta)
    if delta < 1e-10:
        break
    coin_theta = new_coin_theta
    

h_e_record = np.array(h_e_record)
t_e_record = np.array(t_e_record)
theta_record = np.array(theta_record)
delta_record = np.array(delta_record)
    
i, coin_theta, coins

'''
(36,
 array([0.62988197, 0.43099465, 0.84265886, 0.99086422, 0.53815304]),
 [0.84, 0.99, 0.63, 0.44, 0.54])
'''

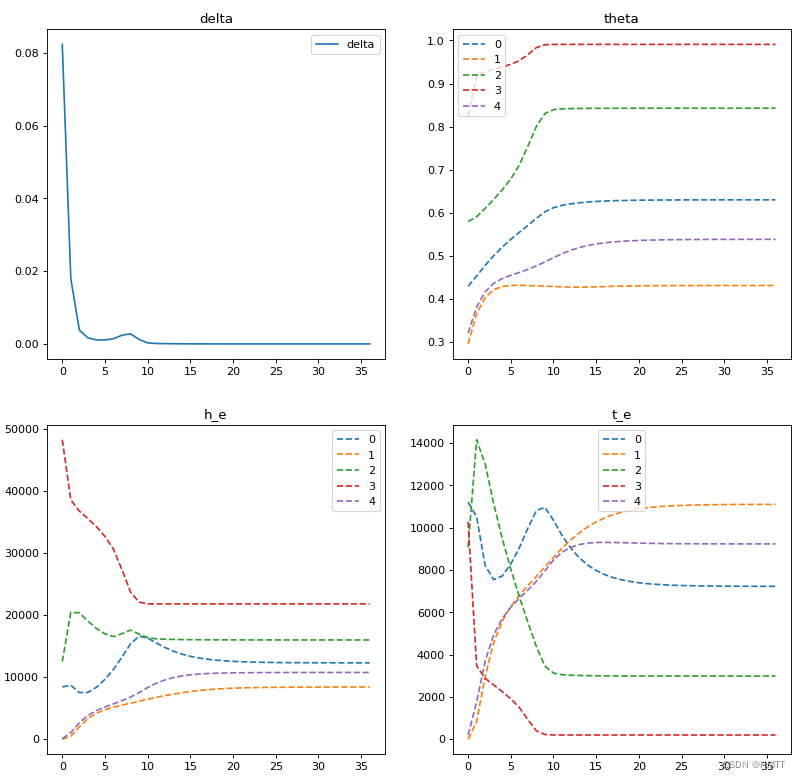
展示参数变化过程

def plot_list(f, x, y, labels, title):
    f.set_title(title)
    for i in range(y.shape[1]):
        f.plot(x, y[:, i], label = labels[i], linestyle='--')

index = range(0, i+1)
labels = list(range(coin_theta.shape[0]))
figure, axes = plt.subplots(2, 2, figsize=(12,12), dpi=80)


axes[0, 0].set_title("delta")
# 与上一步结果的差别
axes[0, 0].plot(index, delta_record, label="delta")
# 硬币正面的概率
plot_list(axes[0, 1], index, theta_record, labels=labels, title="theta")
# 每个硬币正面的加权和
plot_list(axes[1, 0], index, h_e_record, labels=labels, title="h_e")
# 每个硬币反面的加权和
plot_list(axes[1, 1], index, t_e_record, labels=labels, title="t_e")

for axe in axes:
    for a in axe:
        a.legend()