题目1

给定一个有序数组arr，给定一个正数aim

(1)返回累加和为aim的，所有不同二元组

(2)返回累加和为aim的，所有不同三元组

问题一

暴力的解法就是 遍历每一个二元组 找和为aim的

当然 只用暴力解很难ac 想一想有序 那肯定就是能加速 我们可以选择 先抓住一个数 然后另一个数用二分查找 确实把复杂度从O(N²)缩小到 O(N*logN)

解题的时候还想过用单调栈或者滑动窗口 不过这个答案又不一定是连续的 只能作罢

预处理累加数组 也不能加速查找

更好的做法是 双指针法 左右指针分别放在0位置和N-1位置 那么是有序的数组 所以可以让左指针右移让整体和增加 右指针左移 让整体和减少 复杂度为O(N)

捋一下做法

(1)当sum<aim 左指针右移

(2)sum>aim 右指针左移

(3)sum == aim 左指针右移和左指针右移都可以 本质上来讲就是换一种尝试

public static void selectTwo(int [] arr,int aim) {
		int left = 0;
		int right = arr.length-1;
		int sum = 0;
		while(left<=right-1) {
			sum = arr[left] + arr[right];
			if(sum<aim) {
				left++;
			}
			if(sum>aim) {
				right--;
			}
			if(sum==aim) {
				System.out.println(arr[left]+"  "+arr[right]);
				left++;
			}
		}
	}

问题二

简单 先以选定每一个数为 三元组中第一个数 然后转化为二元问题

	public static void selectTwo(int [] arr,int aim,int i,int index) {
		int left = i;
		int right = arr.length-1;
		int sum = 0;
		while(left<=right-1) {
			sum = arr[left] + arr[right];
			if(sum<aim) {
				left++;
			}
			if(sum>aim) {
				right--;
			}
			if(sum==aim) {
				System.out.println(index+" "+arr[left]+"  "+arr[right]);
				left++;
			}
		}
	}
	private static void selectThree(int [] arr,int aim) {
		for(int i = 0;i<=arr.length-1;i++) {
			selectTwo(arr, aim-arr[i],i,arr[i]);
		}
		

题目二

问题一

给定一个数组arr，已知其中所有的值都是非负的，将这个数组看作一个容器，请返回容器能装多少水比如，arr={3,1,2,5,2,4)，根据值画出的直方图就是容器形状，该容器可以装下5格水再比如，arr={4,5,1,3,2}，该容器可以装下2格水

遍历每一个位置可以装多少水 当前位置的装水数就是 左侧的最大值和右侧的最大值取最小值 再减去当前高度 然后如果是负数就不考虑(这是考虑了一种 当前位置一柱擎天的可能性 如果它比其他位置高的很多 也是放不了水的)最左侧和最右侧的格子上面肯定放不了水

用最大值数组 代替遍历行为

我刚开始确实想到用预处理数组了 但是咋想咋不对 你说那左侧右侧最大值 那不得分一个左侧最大值数组 再分一个右侧最大值数组 每个位置的最大值还不同 那不就是遍历了吗 后来看了答案想出来了 先来一个正序的最大值数组 那么当前位置的左侧最大高度就是当前的位置的值

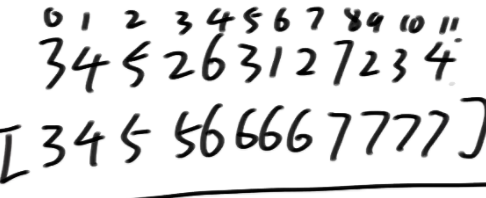
再来一个逆序的数组

3 4 5 2 6 3 1 2 7 2 3 4

7 7 7 7 7 7 7 7 7 4 4 4 

右侧最大值就是当前位置

比如说5位置上的最大放水数

那就是6 7比较小的 也就是6 

public static int MaxWater(int [] arr) {
		int N = arr.length;
		int [] leftside = new int [N];
		int [] rightside = new int [N];
		leftside[0] = arr[0];
		rightside[N-1] =  arr[N-1];
		int sum = 0;
		for(int i = 1;i<N;i++) {
			leftside[i] = Math.max(arr[i],leftside[i-1]);
		}
		for(int i = N-2;i>=0;i--) {
			rightside[i] = Math.max(arr[i],rightside[i+1]);
		}
		for(int i = 1;i<N-1;i++) {
			int tmp = Math.min(leftside[i], rightside[i])-arr[i];
			if(tmp>0) {
				sum += tmp;
			}
		}
		return sum;
	}

这个方法需要两个临时数组的空间 且遍历三遍N大小的数组

吾有一言:一个算法要么对空间不友好 要么对时间不友好 要么对我的脑子不友好 三者至少取其二

所以下面还有一个优化解法

我们这次不需要临时数组 只需要双指针 左指针从1位置开始 右指针从N-2位置开始 再用leftmax记录当前左指针左侧目前最大值 再用rightmax记录当前右指针右侧最大值

对于左指针来说 如果它当前的左边的最大值(leftmax) 小于 右侧目前指针的最大值(rightmax) 右侧目前指针最大值为N 那么接下来的值 如果小于N 那么接下来的位置不会被更新为最大值 如果大于N 那更大于左边了 所以在这种情况 左边的值一定是最大值中的最小值

那如果leftmax > rightmax 是不是就啥都说明不了了呢 确实是这样的 但是我们可以反过来看 rightmax<leftmax了 这又可以执行上面的逻辑

当一个位置的水数判断完后 就把指针向下一个位置推动 判断下一个位置即可

public static int water2(int[] arr) {
		if (arr == null || arr.length < 2) {
			return 0;
		}
		int N = arr.length;
		int L = 1;
		int leftMax = arr[0];
		int R = N - 2;
		int rightMax = arr[N - 1];
		int water = 0;
		while (L <= R) {
			if (leftMax <= rightMax) {
				water += Math.max(0, leftMax - arr[L]);
				leftMax = Math.max(leftMax, arr[L++]);
			} else {
				water += Math.max(0, rightMax - arr[R]);
				rightMax = Math.max(rightMax, arr[R--]);
			}
		}
		return water;
	}

二维装水问题

就是给一个二维数组 其他和上一题一样

你或许会想把它拆成多个一维的 但是不完全是这样 假如拆成一列一列的话 还要受行上面的限制

那么暴力解法就是 把按行拆的结果放进二维数组中 再把按列拆的结果放进二维数组中 然后遍历两个数组 取每个位置上的更小值作为当前位置的结果 然后再累加 费老劲了

优化做法 说实话已经和一维的一点关系没有了

遍历它的外面一圈 把它放到小根堆中 然后弹出堆顶元素 然后把这个元素作为max 然后把它的上下左右四个位置加入到小根堆中  并结算当前位置水数(由于这个位置就是max 所以没有水) 然后以此类推 弹出堆顶 结算水数 然后把上下左右没加入过的位置加到小根堆中 直到弹出的值比当前max 大 那么就把max替换掉 接着刚才的操作 直到堆中没有任何元素

本质上很简单 先把最外面的一圈遍历了 找到第一个缺口(最小值) 如果没有任何缺口也无所谓 随便找一个地方开始行动 然后找到了这个点呢 就用感染算法看它的前后左右 如果比这个点低的话就说明这个地方有水 遍历这个坑 (因为最开始都是把最外面的一圈给加进小根堆 所以下一个弹出的 一定是刚才加入的较小值 如果大的话不会跑到小根堆顶 不要担心从另一边全部漏走的可能性 因为当前我们拿到的点就是最小值) 然后这个坑遍历完了呢 就会换max 换max就是换了个坑的意思

public static int MaxWater(int [][] arr) {
		if(arr==null||arr.length==0||arr[0].length==0) {
			return 0;
		}
		int N = arr.length;
		int M = arr[0].length;
	   boolean [][] has = new boolean [N][M];
	   PriorityQueue<Node> queue = new PriorityQueue<Node>(new mycompare());
	   for(int i = 0;i<M;i++) {
		   queue.add(new Node(0, i, arr[0][i]));
		   has[0][i] = true;
	   }
	   for(int i = 0;i<M;i++) {
		   queue.add(new Node(N-1, i, arr[N-1][i]));
		   has[0][i] = true;
	   }
	   for(int i = 1;i<N-1;i++) {
		   queue.add(new Node(i, 0, arr[i][M-1]));
		   has[i][M-1] = true;
	   }
	   for(int i = 1;i<N-1;i++) {
		   queue.add(new Node(i, M-1, arr[i][0]));
		   has[i][M-1] = true;
	   }
	   int max = Integer.MIN_VALUE;
	   int sum = 0;
	   while(!queue.isEmpty()) {
		   Node node = queue.poll();
		   int row = node.row;
		   int col = node.col;
		   int val = node.value;
		   max = Math.max(max,val);
		   
		   if(row-1>=0&&has[row-1][col]==false) {
			   queue.add(new Node(row-1,col,arr[row-1][col]));
			   has[row-1][col] = true;
               if(max-arr[row-1][col]>0) {
			   sum += max-arr[row-1][col];
		   }
		   }
		   if(col-1>=0&&has[row][col-1]==false) {
			   queue.add(new Node(row,col-1,arr[row][col-1]));
			   has[row][col-1] = true;
               if(max-arr[row][col-1]>0) {
			   sum += max-arr[row][col-1];
		   }
		   }
		   if(row+1<N&&has[row+1][col]==false) {
			   queue.add(new Node(row+1,col,arr[row+1][col]));
			   has[row+1][col]= true;
               if(max-arr[row+1][col]>0) {
			   sum += max-arr[row+1][col];
		   }
		   }
		   if(col+1<M&&has[row][col+1]==false) {
			   queue.add(new Node(row+1,col,arr[row][col+1]));
			   has[row][col+1] = true;
                if(max-arr[row][col+1]>0) {
			   sum += max-arrarr[row][col+1];
		   }
		   }		   
	   }
	   return sum;
	}

 刚开始加边界的时候 只加了右侧和上侧 忘记还有两边了

再有 每次应在加入节点时计算水 而不是弹出节点时计算水 我没想明白为啥 虽然没想明白弹出时有啥问题 但还是先这么写吧