2673. 使二叉树所有路径值相等的最小代价

题目描述

给你一个整数 n 表示一棵 满二叉树 里面节点的数目，节点编号从 1 到 n 。根节点编号为 1 ，树中每个非叶子节点 i 都有两个孩子，分别是左孩子 2 * i 和右孩子 2 * i + 1 。

树中每个节点都有一个值，用下标从 0 开始、长度为 n 的整数数组 cost 表示，其中 cost[i] 是第 i + 1 个节点的值。每次操作，你可以将树中 任意 节点的值 增加 1 。你可以执行操作 任意 次。

你的目标是让根到每一个 叶子结点 的路径值相等。请你返回 最少 需要执行增加操作多少次。

注意：

满二叉树 指的是一棵树，它满足树中除了叶子节点外每个节点都恰好有 2 个节点，且所有叶子节点距离根节点距离相同。
路径值 指的是路径上所有节点的值之和。

示例 1：

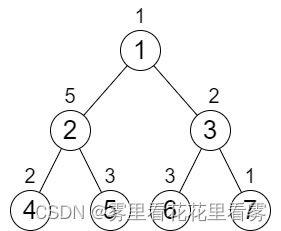
输入：n = 7, cost = [1,5,2,2,3,3,1]
输出：6
解释：我们执行以下的增加操作：
- 将节点 4 的值增加一次。
- 将节点 3 的值增加三次。
- 将节点 7 的值增加两次。
从根到叶子的每一条路径值都为 9 。
总共增加次数为 1 + 3 + 2 = 6 。
这是最小的答案。

示例 2：

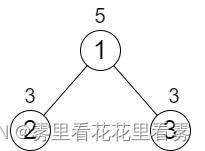
输入：n = 3, cost = [5,3,3]
输出：0
解释：两条路径已经有相等的路径值，所以不需要执行任何增加操作。

提示：

3 <= n <= 105
n + 1 是 2 的幂
cost.length == n
1 <= cost[i] <= 104

解题思路

思路：刚刚那题让我想到了这一题，虽然不太像，但是都是二叉树上的问题。要使得二叉树所有路径值相等的最小代价，那必定是从下往上更新，对于叶子节点，即将两者均更新为其中的最大值，其需要的代价是两者之间的差值绝对值，然后再将这个最大值传递到上方，依次类推。

int minIncrements(int n, vector<int>& cost) 
{
   // 满二叉树 可以使用数组表示
   int ans=0; //表示最少操作次数
   for(int i=n/2;i>0;i--) //i表示节点编号 如果对应数组的话要减一
   {
      ans+=abs(cost[2*i-1]-cost[2*i]);  //取兄弟节点的差值绝对值
      cost[i-1]+=min(cost[2*i-1],cost[2*i]); //将子节点代价加上
   }
   return ans;
}

总结：挺巧妙的！