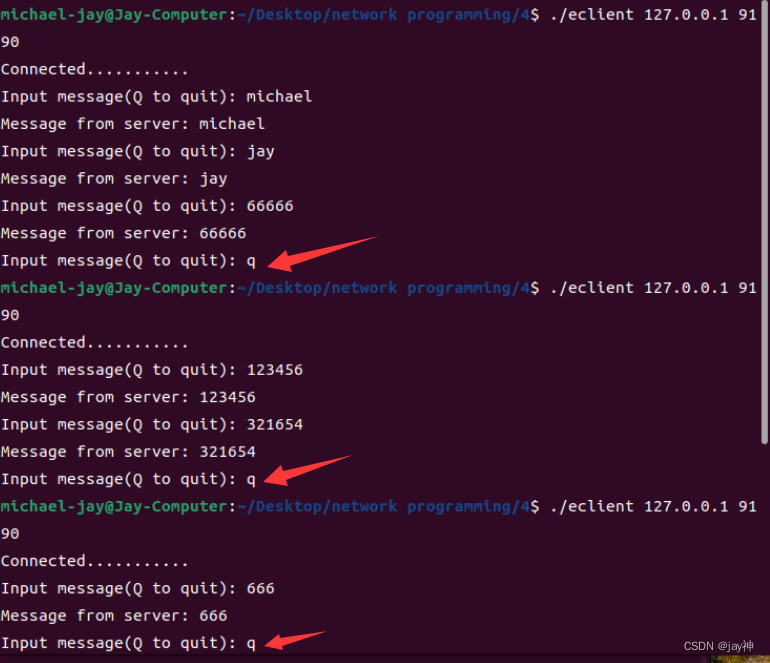
【R语言】机器学习-手撕逻辑回归

算法原理

逻辑回归是一种常用的分类算法，它在机器学习领域有着广泛的应用。在介绍具体的实现细节之前，我们先来了解一下逻辑回归的算法原理。

sigmoid函数

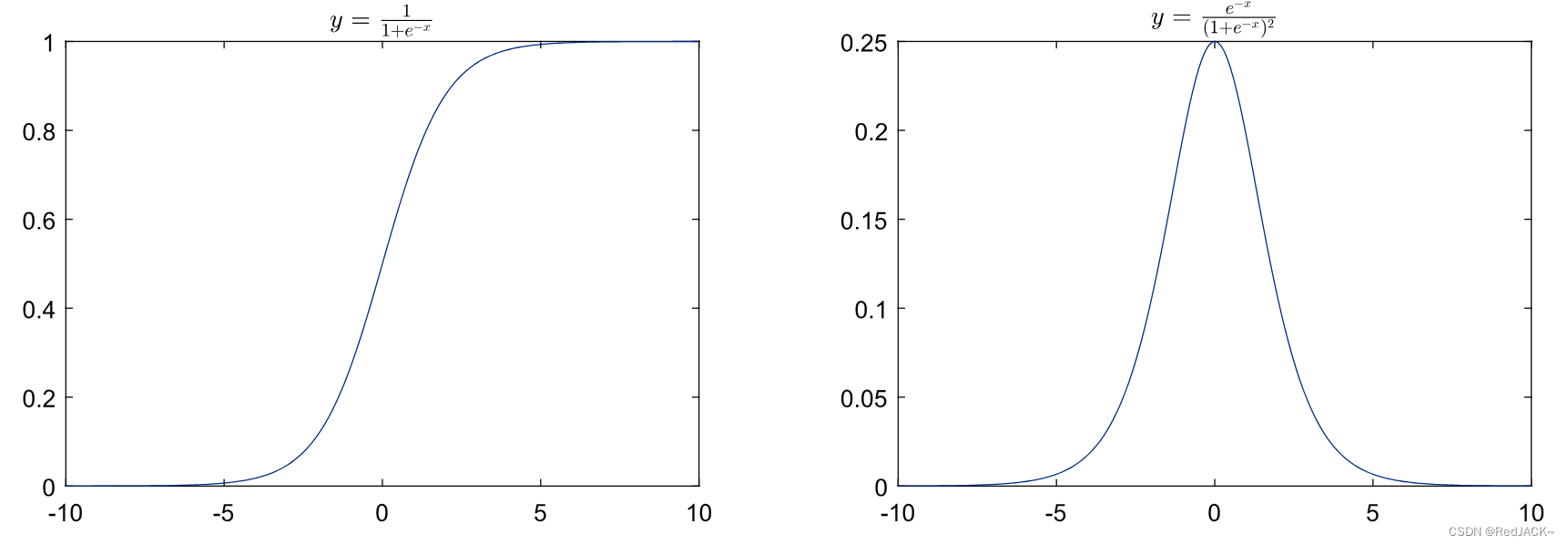
逻辑回归使用sigmoid函数（也称为逻辑函数）来进行分类。Sigmoid函数是一个S形曲线，它将输入值映射到0和1之间的概率值。它的定义如下：
$$S(x)=\frac{1}{1+e^{-x}}$$
其函数图像与导函数图像如下：

广义线性模型

逻辑回归是一种广义线性模型（Generalized Linear Model，简称GLM）。广义线性模型是一类包括逻辑回归在内的统计模型，它通过线性组合输入特征，并通过一个链接函数将线性组合映射到输出概率。

线性模型的矩阵表示
$$Z=\mathbf{X}{\theta }^T$$

• 输入的$\mathbf{X}$是$m\times (n+1)$维度的矩阵，$m$是样本数量，$n$是特征数。
• $\theta$是$(n+1)$维的权重向量，其转置${\theta }^T$是$(n+1)\times 1$维度的列矩阵

将线性模型代入sigmoid函数，得逻辑回归的矩阵表示
$$h_{\theta }(\mathbf{X})=\frac{1}{1+e^{-\mathbf{X}{\theta }^T}}$$

• $h_{\theta }(\mathbf{X})$是假设函数（hypothesis function），为$m\times 1$维度的矩阵，代表$m$个样本数据的预测概率值。

极大似然函数

极大似然估计（Maximum Likelihood Estimation，简称MLE）是一种常用的参数估计方法，用于在给定观测数据的情况下，估计出最有可能生成这些观测数据的模型参数值。

对某个多分类问题的数据集$D=\{({\mathbf{x}}_1,y_1),({\mathbf{x}}_2,y_2),\dots ,({\mathbf{x}}_m,y_m)\}$，$\mathbf{x}$为特征向量，其MLE表达式为
$$\begin{array}{rl}L(\mathbf{x},\theta )& =\prod _{i=1}^{m}p(y_i|{\mathbf{x}}_i,\theta )\\ & =p(y_1|{\mathbf{x}}_1,\theta )p(y_2|{\mathbf{x}}_2,\theta )\dots p(y_m|{\mathbf{x}}_m,\theta )\end{array}$$
在逻辑回归中，我们使用极大似然估计来估计模型的参数。极大似然估计的目标是找到一组参数，使得给定观测数据的条件下，观测到这些数据的概率最大化。对于二分类的逻辑回归，其预测值的概率分别可表示为
$$\begin{array}{rl}p(y=1|\mathbf{x})& =\frac{1}{1+e^{-\mathbf{x}{\theta }^T}}\\ p(y=0|\mathbf{x})& =1-p(y=1|\mathbf{x})=\frac{1}{1+e^{\mathbf{x}{\theta }^T}}\end{array}$$
则逻辑回归的最大似然估计可表示为
$$\begin{array}{rl}L(\mathbf{x})& =\prod _{i=1}^{k}p(y_i=1|{\mathbf{x}}_i)\prod _{i=k}^{m}p(y_i=0|{\mathbf{x}}_i)\\ & =\prod _{i=1}^{k}p(y_i=1|{\mathbf{x}}_i)\prod _{i=k}^m\left(1-p(y_i=1|{\mathbf{x}}_i)\right)\end{array}$$
设$h(\mathbf{x})=p(y=1|\mathbf{x})$得
$$L(\mathbf{x})=\prod _{i=1}^{k}h({\mathbf{x}}_i)\prod _{i=k}^m\left(1-h({\mathbf{x}}_i)\right)$$
利用 y ∈ { 0 , 1 } y \in \{0,1\} y∈{0,1}的特征可将上式整理为
$$L(\mathbf{x})=\prod _{i=1}^{m}h({\mathbf{x}}_i{)}^{y_i}(1-h({\mathbf{x}}_i){)}^{1-y_i}$$

损失函数

逻辑回归使用对数似然损失函数（log-likelihood loss）作为优化的目标函数。对数似然损失函数可以衡量模型的预测结果与实际观测值之间的差异。
$$l(\mathbf{x})=\ln L(\mathbf{x})=\sum _{i=1}^m{y}_i\ln (h({\mathbf{x}}_i))+(1-y_i)\ln (1-h({\mathbf{x}}_i))$$
为了结合梯度下降法求解最大似然估计的最大值，我们引入如下损失函数（loss function）
$$J(\theta )=-\frac{1}{m}{l}_{\theta }(\mathbf{x})=-\frac{1}{m}\sum _{i=1}^m{y}_i\ln (h_{\theta }({\mathbf{x}}_i))+(1-y_i)\ln (1-h_{\theta }({\mathbf{x}}_i))$$

梯度下降法

为了最小化损失函数，我们使用梯度下降算法来更新模型参数。梯度下降算法通过计算损失函数对参数的偏导数，并沿着负梯度方向更新参数值，从而逐步优化模型。
$$\begin{array}{rl}J(\theta )& =-\frac{1}{m}\sum _{i=1}^m{y}_i\ln (h_{\theta }({\mathbf{x}}_i))+(1-y_i)\ln (1-h_{\theta }({\mathbf{x}}_i))\\ & =-\frac{1}{m}\sum _{i=1}^m{y}_i\ln (\frac{h_{\theta }({\mathbf{x}}_i)}{1-h_{\theta }({\mathbf{x}}_i)})+\ln (1-h_{\theta }({\mathbf{x}}_i))\end{array}$$
将$h_{\theta }(\mathbf{x})=\frac{1}{1+e^{-\mathbf{x}{\theta }^T}}$代入公式得
$$\begin{array}{rl}J(\theta )& =-\frac{1}{m}\sum _{i=1}^m{y}_i{\mathbf{x}}_i{\theta }^T+\ln (\frac{1}{1+e^{{\mathbf{x}}_i{\theta }^T}})\\ & =-\frac{1}{m}\sum _{i=1}^m{y}_i{\mathbf{x}}_i{\theta }^T-\ln (1+e^{{\mathbf{x}}_i{\theta }^T})\end{array}$$
求解损失函数梯度
$$\begin{array}{rl}\frac{\partial J(\theta )}{\partial \theta }& =-\frac{1}{m}\sum _{i=1}^m{y}_i{\mathbf{x}}_i-\frac{{\mathbf{x}}_i{e}^{{\mathbf{x}}_i{\theta }^T}}{1+e^{{\mathbf{x}}_i{\theta }^T}}\\ & =-\frac{1}{m}\sum _{i=1}^m\left(y_i-\frac{1}{1+e^{-{\mathbf{x}}_i{\theta }^T}}\right){\mathbf{x}}_i\\ & =-\frac{1}{m}\sum _{i=1}^m\left(y_i-h_{\theta }({\mathbf{x}}_i)\right){\mathbf{x}}_i\end{array}$$
梯度下降迭代关系式为
$${\theta }^{(i+1)}={\theta }^{(i)}-\alpha \cdot \frac{\partial J(\theta )}{\partial \theta }$$

• $\alpha$为学习率（步长）

求解梯度函数也可用矩阵表示为
$$\frac{\partial J(\theta )}{\partial \theta }=-\frac{1}{m}{\mathbf{X}}^T\left(\mathbf{Y}-h_{\theta }(\mathbf{X})\right)$$

• $\mathbf{X}$是$m\times (n+1)$维度的矩阵
• $\mathbf{Y}$是$m\times 1$维度的矩阵

算法实现

模型训练

# 定义逻辑回归函数
logistic_regression <- function(data, epochs, learning_rate) {
  # 初始化权重和偏置
  w <- matrix(0, nrow = ncol(data) - 1, ncol = 1)
  b <- 0
  
  # 迭代更新权重和偏置
  for (epoch in 1:epochs) {
    # 计算线性模型的输出
    z <- as.matrix(data[, -ncol(data)]) %*% w + b
    # 应用逻辑函数
    a <- 1 / (1 + exp(-z))
    
    # 计算损失函数的梯度
    dw <- t(as.matrix(data[, -ncol(data)])) %*% (a - data[, ncol(data)]) / nrow(data)
    db <- sum(a - data[, ncol(data)]) / nrow(data)
    
    # 更新权重和偏置
    w <- w - learning_rate * dw
    b <- b - learning_rate * db
  }
  
  # 返回训练好的权重和偏置
  return(list("weights" = w, "bias" = b))
}

模型预测

# 使用训练好的模型进行预测
predict_logistic_regression <- function(model, new_data) {
  # 提取权重和偏置
  w <- model$weights
  b <- model$bias
  
  # 计算线性模型的输出
  z <- as.matrix(new_data) %*% w + b
  # 应用逻辑函数
  a <- 1 / (1 + exp(-z))
  
  # 将概率转换为分类标签
  predictions <- ifelse(a > 0.5, 1, 0)
  
  # 返回预测结果
  return(predictions)
}

完整代码

# 创建一个示例数据集
data <- data.frame(
  x1 = c(1, 2, 3, 4, 5),
  x2 = c(2, 4, 6, 8, 10),
  y = c(0, 0, 0, 1, 1)
)

# 定义逻辑回归函数
logistic_regression <- function(data, epochs, learning_rate) {
  # 初始化权重和偏置
  w <- matrix(0, nrow = ncol(data) - 1, ncol = 1)
  b <- 0
  
  # 迭代更新权重和偏置
  for (epoch in 1:epochs) {
    # 计算线性模型的输出
    z <- as.matrix(data[, -ncol(data)]) %*% w + b
    # 应用逻辑函数
    a <- 1 / (1 + exp(-z))
    
    # 计算损失函数的梯度
    dw <- t(as.matrix(data[, -ncol(data)])) %*% (a - data[, ncol(data)]) / nrow(data)
    db <- sum(a - data[, ncol(data)]) / nrow(data)
    
    # 更新权重和偏置
    w <- w - learning_rate * dw
    b <- b - learning_rate * db
  }
  
  # 返回训练好的权重和偏置
  return(list("weights" = w, "bias" = b))
}

# 使用逻辑回归函数进行训练
epochs <- 1000
learning_rate <- 0.01
model <- logistic_regression(data, epochs, learning_rate)

# 输出训练得到的权重和偏置
print(model)

# 使用训练好的模型进行预测
predict_logistic_regression <- function(model, new_data) {
  # 提取权重和偏置
  w <- model$weights
  b <- model$bias
  
  # 计算线性模型的输出
  z <- as.matrix(new_data) %*% w + b
  # 应用逻辑函数
  a <- 1 / (1 + exp(-z))
  
  # 将概率转换为分类标签
  predictions <- ifelse(a > 0.5, 1, 0)
  
  # 返回预测结果
  return(predictions)
}

# 创建一个新的数据集用于预测
new_data <- data.frame(
  x1 = c(3, 4),
  x2 = c(5, 6)
)

# 使用训练好的模型进行预测
predictions <- predict_logistic_regression(model, new_data)

# 输出预测结果
print(predictions)