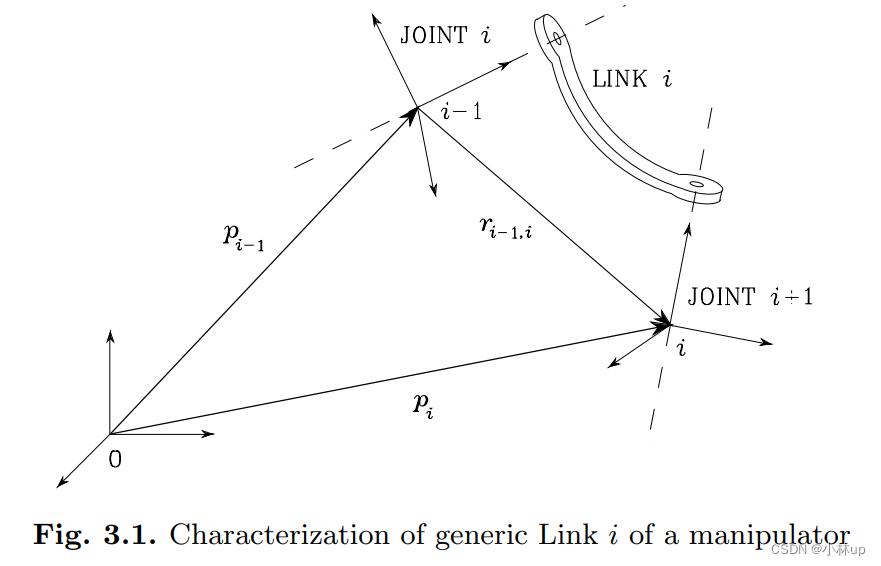
1. 线速度和角速度的递推通式推导

$${\mathbf{p}}_i={\mathbf{p}}_{i-1}+{\mathbf{R}}_{i-1}{\mathbf{r}}_{i-1,i}^{i-1}$$

${\mathbf{p}}_{i-1}$是 { i − 1 } \{i-1\} {i−1}坐标系的原点的向量，${\mathbf{p}}_i$是 { i } \{i\} {i}坐标系的原点的向量，对于向量如果没有上标默认在 { 0 } \{0\} {0}坐标系下表示(往后向量不说在哪个坐标系下表示默认是在 { 0 } \{0\} {0}坐标系下表示)。${\mathbf{r}}_{i-1,i}^{i-1}$是 { i } \{i\} {i}坐标系的原点相对于 { i − 1 } \{i-1\} {i−1}坐标系的原点构成的位置向量，这个向量在 { i − 1 } \{i-1\} {i−1}坐标系下表示。对上式求导：

$${\dot{\mathbf{p}}}_i={\dot{\mathbf{p}}}_{i-1}+{\mathbf{R}}_{i-1}{\dot{\mathbf{r}}}_{i-1,i}^{i-1}+{\omega }_{i-1}\times {\mathbf{R}}_{i-1}{\mathbf{r}}_{i-1,i}^{i-1}={\dot{\mathbf{p}}}_{i-1}+{\mathbf{v}}_{i-1,i}+{\omega }_{i-1}\times {\mathbf{r}}_{i-1,i}$$

上式中，${\mathbf{v}}_{i-1,i}$是 { i } \{i\} {i}坐标系的原点相对于 { i − 1 } \{i-1\} {i−1}坐标系的原点构成的线速度向量。

对于旋转矩阵，我们有：

$${\mathbf{R}}_i={\mathbf{R}}_{i-1}{\mathbf{R}}_i^{i-1}$$

对旋转矩阵求导我们有：$\dot{\mathbf{R}}(t)=\mathbf{S}(t)\mathbf{R}(t)$，其中$\mathbf{S}(t)$是一个反对称矩阵，带入上式我们有：

$$\mathbf{S}({\mathbf{\omega }}_i){\mathbf{R}}_i=\mathbf{S}({\mathbf{\omega }}_{i-1}){\mathbf{R}}_i+{\mathbf{R}}_{i-1}\mathbf{S}({\mathbf{\omega }}_{i-1,i}^{i-1}){\mathbf{R}}_i^{i-1}$$

上式中，${\omega }_{i-1,i}^{i-1}$是 { i } \{i\} {i}坐标系的原点相对于 { i − 1 } \{i-1\} {i−1}坐标系的原点构成的角速度向量，这个向量在 { i − 1 } \{i-1\} {i−1}坐标系下表示。

由于旋转矩阵是正交矩阵：

$${\mathbf{R}}_{i-1}\mathbf{S}\left({\mathbf{\omega }}_{i-1,i}^{i-1}\right){\mathbf{R}}_i^{i-1}={\mathbf{R}}_{i-1}\mathbf{S}({\mathbf{\omega }}_{i-1,i}^{i-1}){\mathbf{R}}_{i-1}^T{\mathbf{R}}_{i-1}{\mathbf{R}}_i^{i-1}$$

这里使用公式$\mathbf{RS}(\omega ){\mathbf{R}}^T=\mathbf{S}(\mathbf{R}\omega )$，我们有：

$${\mathbf{R}}_{i-1}\mathbf{S}({\mathbf{\omega }}_{i-1,i}^{i-1}){\mathbf{R}}_i^{i-1}=\mathbf{S}({\mathbf{R}}_{i-1}{\mathbf{\omega }}_{i-1,i}^{i-1}){\mathbf{R}}_i$$

于是前面的式子变成：

$$\mathbf{S}({\mathbf{\omega }}_i){\mathbf{R}}_i=\mathbf{S}({\mathbf{\omega }}_{i-1}){\mathbf{R}}_i+\mathbf{S}({\mathbf{R}}_{i-1}{\mathbf{\omega }}_{i-1,i}^{i-1}){\mathbf{R}}_i$$

于是我们有：

$${\mathbf{\omega }}_i={\mathbf{\omega }}_{i-1}+{\mathbf{R}}_{i-1}{\mathbf{\omega }}_{i-1,i}^{i-1}={\mathbf{\omega }}_{i-1}+{\mathbf{\omega }}_{i-1,i}=$$

总结我们得到的线速度和角速度的递推通式为：

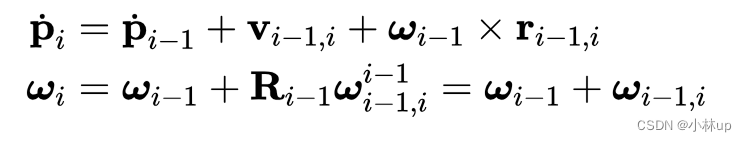
1.1 平移副情况

对于平移副，我们有角速度：

$${\mathbf{\omega }}_{i-1,i}=0$$

线速度：

$${\mathbf{v}}_{i-1,i}={\dot{d}}_i{\mathbf{z}}_{i-1}$$

${\mathbf{z}}_{i-1}$是 { i − 1 } \{i-1\} {i−1}坐标系沿着$\mathbf{z}$轴的单位向量。

带入前面的公式我们有：

$$\begin{array}{rl}{\mathbf{\omega }}_i& ={\mathbf{\omega }}_{i-1}\\ {\dot{\mathbf{p}}}_i& ={\dot{\mathbf{p}}}_{i-1}+{\dot{d}}_i{\mathbf{z}}_{i-1}+{\mathbf{\omega }}_i\times {\mathbf{r}}_{i-1,i}\end{array}$$

1.2 旋转副情况

对于旋转副，我们有角速度：

$${\mathbf{\omega }}_{i-1,i}={\dot{\vartheta }}_i{\mathbf{z}}_{i-1}$$

$${\mathbf{v}}_{i-1,i}={\mathbf{\omega }}_{i-1,i}\times {\mathbf{r}}_{i-1,i}$$

于是我们有：

$$\begin{array}{rl}{\mathbf{\omega }}_i& ={\mathbf{\omega }}_{i-1}+{\dot{\vartheta }}_i{\mathbf{z}}_{i-1}\\ {\dot{\mathbf{p}}}_i& ={\dot{\mathbf{p}}}_{i-1}+{\mathbf{\omega }}_i\times {\mathbf{r}}_{i-1,i}\end{array}$$

2. 雅克比矩阵计算

2.1 线速度雅克比分量

$${\dot{\mathbf{p}}}_e=\sum _{i=1}^n\frac{\partial {\mathbf{p}}_e}{\partial q_i}{\dot{q}}_i=\sum _{i=1}^n{\mathbf{J}}_{Pi}{\dot{q}}_i$$

上式可以看到，末端的线速度都是由每个关节的线速度贡献的，其中${\dot{q}}_i$是关节速度。

2.1.1 平移副情况

对于平移副我们有$q_i=d_i$：

根据：

$${\mathbf{v}}_{i-1,i}={\dot{d}}_i{\mathbf{z}}_{i-1}$$

$${\dot{q}}_i{\mathbf{J}}_{Pi}={\dot{d}}_i{\mathbf{z}}_{i-1}$$

于是我们有:

$${\mathbf{J}}_{Pi}={\mathbf{z}}_{i-1}$$

2.1.2 旋转副情况

对于旋转副我们有$q_i={\theta }_i$:

$${\dot{q}}_i{\mathbf{J}}_{Pi}={\mathbf{\omega }}_{i-1,i}\times {\mathbf{r}}_{i-1,e}={\dot{\vartheta }}_i{\mathbf{z}}_{i-1}\times \left({\mathbf{p}}_e-{\mathbf{p}}_{i-1}\right)$$

于是：

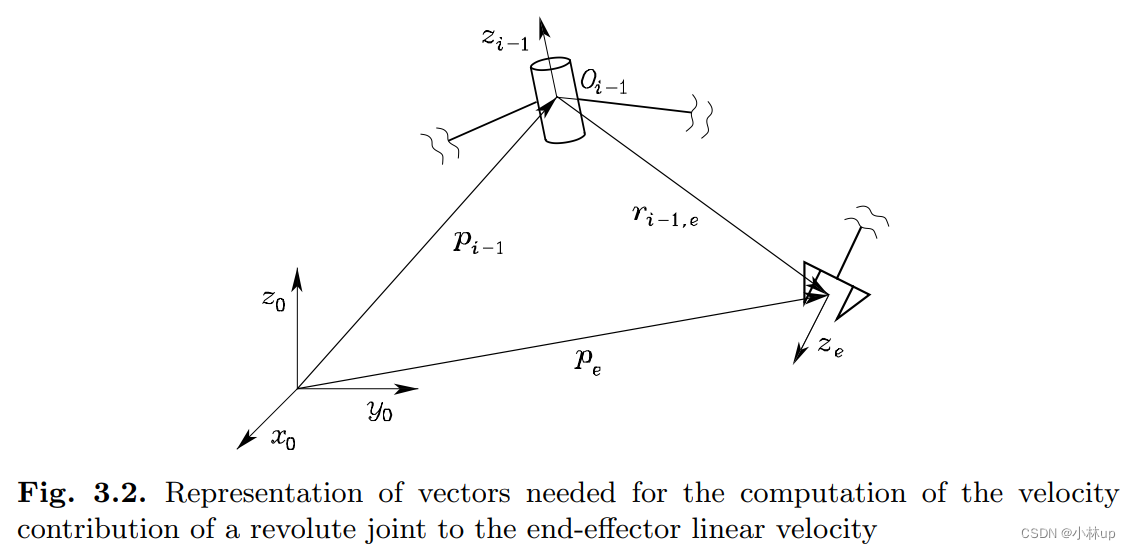
$${\mathbf{J}}_{Pi}={\mathbf{z}}_{i-1}\times \left({\mathbf{p}}_e-{\mathbf{p}}_{i-1}\right)$$

2.2 角速度雅克比分量

对于角速度我们有：

$${\mathbf{\omega }}_e={\mathbf{\omega }}_n=\sum _{i=1}^n{\mathbf{\omega }}_{i-1,i}=\sum _{i=1}^n{\mathbf{J}}_{Oi}{\dot{q}}_i$$

2.2.1 平移副情况

对于平移副我们有$q_i=d_i$：

$${\dot{q}}_i{\mathbf{J}}_{Oi}=0$$

于是有：

$${\mathbf{ȷ}}_{Oi}=0$$

2.2.2 旋转副情况

对于旋转副我们有$q_i={\theta }_i$:

$${\dot{q}}_i{\mathbf{J}}_{Oi}={\dot{\vartheta }}_i{\mathbf{z}}_{i-1}$$

于是有：

$${\mathbf{J}}_{Oi}={\mathbf{z}}_{i-1}$$

2.3 雅可比矩阵综合

我们可以把线速度和角速度的雅克比矩阵的分量合成，于是我们有：

$$\mathbf{J}=\left[\begin{array}{lll}{\mathbf{J}}_{P1}& & {\mathbf{J}}_{Pn}\\ & \dots & \\ {\mathbf{J}}_{O1}& & {\mathbf{J}}_{On}\end{array}\right]$$

可以分成平移副和旋转副来讨论雅克比矩阵中的分量：

$$\left[\begin{array}{l}{\mathbf{J}}_{Pi}\\ {\mathbf{J}}_{Oi}\end{array}\right]=\{\begin{array}{ll}\left[\begin{array}{c}{\mathbf{z}}_{i-1}\\ 0\end{array}\right]& \text{ 平移副 }\\ \left[\begin{array}{c}{\mathbf{z}}_{i-1}\times \left({\mathbf{p}}_e-{\mathbf{p}}_{i-1}\right)\\ {\mathbf{z}}_{i-1}\end{array}\right]& \text{ 旋转副 }\end{array}$$

关于上式的${\mathbf{z}}_{i-1}$、${\mathbf{p}}_e$、${\mathbf{p}}_{i-1}$计算如下：

3. 不同坐标系下雅克比矩阵的转换

不同坐标系下线速度和加速度的转换如下：

$$\left[\begin{array}{c}{\dot{\mathbf{p}}}_e^u\\ {\mathbf{\omega }}_e^u\end{array}\right]=\left[\begin{array}{cc}{\mathbf{R}}^u& 0\\ 0& {\mathbf{R}}^u\end{array}\right]\left[\begin{array}{c}{\dot{\mathbf{p}}}_e\\ {\mathbf{\omega }}_e\end{array}\right],$$

于是有：

$$\left[\begin{array}{c}{\dot{\mathbf{p}}}_e^u\\ {\mathbf{\omega }}_e^u\end{array}\right]=\left[\begin{array}{cc}{\mathbf{R}}^u& 0\\ 0& {\mathbf{R}}^u\end{array}\right]\mathbf{J}\dot{\mathbf{q}}$$

则有：

$${\mathbf{J}}^u=\left[\begin{array}{cc}{\mathbf{R}}^u& 0\\ 0& {\mathbf{R}}^u\end{array}\right]\mathbf{J}$$

这里的${\mathbf{J}}^u$就是在 { u } \{u\} {u}坐标系下表示的雅克比矩阵。

参考资料

[1]Siciliano B, Sciavicco L, Villani L, et al. . Robotics: Modelling, Planning and Control, 106-113