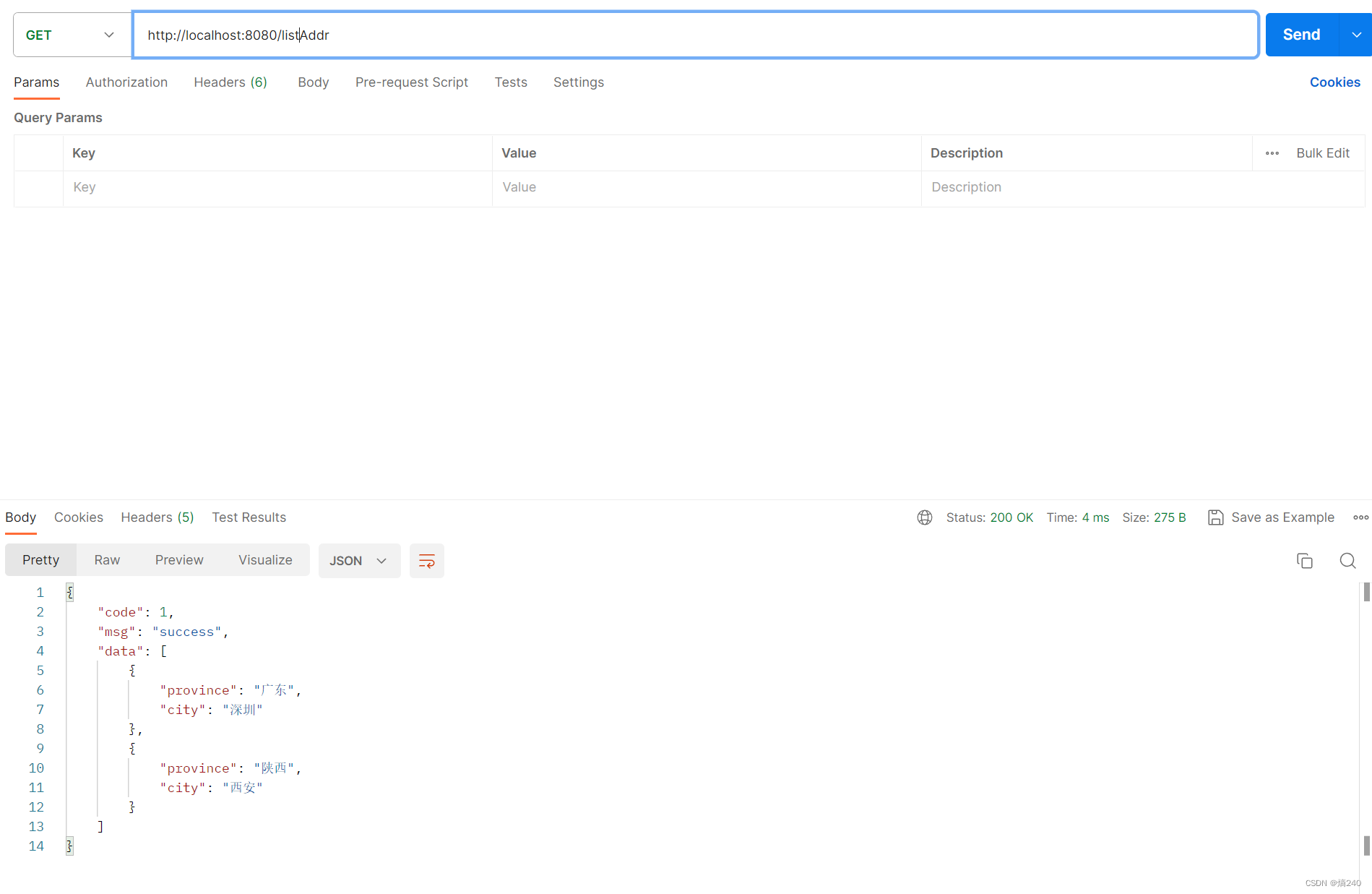
原文链接:https://blog.csdn.net/xzerui/article/details/118684260
一、基本概念
单调队列是指:单调递增或单调递减的队列。所以它也有如下几个性质:
1.队列中的元素在原来的列表中的位置是由前往后的(随着循环顺序入队)。
2.队列中元素的大小是单调递增或递减的。
3.从队尾入列,队首或队尾出列
时间复杂度:O(N)
二、例题
1.最大子序和(dp+单调队列优化)
题目描述
输入一个长度为n的整数序列,从中找出一段不超过m的连续子序列,使得整个序列的和最大。
例如 1,-3,5,1,-2,3
当m=4时,S=5+1-2+3=7
当m=2或m=3时,S=5+1=6
输入
第一行两个数n,m(n,m≤300000)(n,m \leq 300000)(n,m≤300000)
第二行有n个数,要求在n个数找到最大子序和
输出
一个数,数出他们的最大子序和
样例输入
6 4
1 -3 5 1 -2 3
样例输出
7
题解:
计算区间和的问题,一般转化为连个前缀和相减的形式进行求解。我们可以先求出S[i]表示序列里前i ii项的和,则连续子序列[L,R]中的和就等于S [ R ] − S [ L − 1 ].所以我们可以非常巧妙地将原问题转化为:找出两个位子h和t,使S [ h ] − S [ t ] 最大并且h − t < = m
首先枚举右端点i,当i固定时,问题就变为:找到一个右端点j,其中j属于[ i − m , i − 1 ]这个集合,并且S [ j ]最小.
如果我们比较一下任意的两个位子j和k,如果k<j<i,并且S[k]>=S[j],那么对于所有大于等于i的右端点,k永远不会成为最佳选择。这是因为不但S[k]不小于S[j],而且j离i更近,长度更不容易超过M,即j的生存能力比k更强。所以当j出现后,k就是个完全无用的位子。
以上比较可以让我们得出结论:可能成为最优选择的策论集合一定是一个"下标位置递增、对应的前缀和S的值也递增"的序列。我们可以用一个队列保存这个序列。随着右端点变从前向后扫描,我们对于每个i可以执行以下步骤:
- 1.判断队头决策与i的距离是否超过M的范围,若超则出队
- 2.此时队头就是右端点i时,左端点j的最优选择
- 3.不断删除队尾决策,直到队尾对应的S值小于S[i]。然后把i作为一个新的决策入队
public class Main {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt(),m=sc.nextInt();
sc.nextLine();
int[] nums=new int[n+1];
nums[0]=0;
for(int i=1;i<=n;i++){
nums[i]=sc.nextInt()+nums[i-1];
}
Deque<Integer> deque=new ArrayDeque<>();
deque.addFirst(0);
int ans= Integer.MIN_VALUE;
for(int i=1;i<=n;i++){
while(!deque.isEmpty()&&(i-deque.getFirst())>m) deque.removeFirst();
ans=Math.max(ans,nums[i]-nums[deque.getFirst()]);
while(!deque.isEmpty()&&nums[deque.getLast()]>nums[i]) deque.removeLast();
deque.addLast(i);
}
System.out.println(ans);
}
}
2.滑动窗口
题目描述
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
示例 2:
输入:nums = [1], k = 1
输出:[1]
提示:
1 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4
1 <= k <= nums.length
题解:
用暴力作法,需要O(nk)的时间复杂度,为了优化降低时间复杂度,可以用单调队列遍历整个数组,找最小值时将前面比新加入的数大的数都删去,每次只取队头,可以将时间复杂度降低到O(n).
步骤:
①用一个数组来存储输入的数,用另一个数组存储每个元素在原数组中的下标。
②分为找最大值和找最小值两步来写。
注意事项:
①q数组存储的是原数组中的下标
②注意过程中一些变量的初始值为零,有的地方要加1
③注意什么时候用队头,什么时候用队尾
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
//记录窗口内最大值和其位置,每次移动后需要比较窗口内最大值和新值之间的关系
if(k==1) return nums;
int n=nums.length;
int[] res=new int[n-k+1];
//赋初值
Deque<Integer> deque=new ArrayDeque<>();
deque.addFirst(0);
for(int i=1;i<k;i++){
while(!deque.isEmpty()&&nums[deque.getLast()]<nums[i]){
deque.removeLast();
}
deque.addLast(i);
}
res[0]=nums[deque.getFirst()];
for(int i=1;i<n-k+1;i++){
while(!deque.isEmpty()&&(i>deque.getFirst())){
deque.removeFirst();
}
res[i]=Math.max(nums[deque.getFirst()],nums[i+k-1]);
while(!deque.isEmpty()&&(nums[i+k-1]>nums[deque.getLast()])){
deque.removeLast();
}
deque.addLast(i+k-1);
}
//如果i-deque.getFirst()>=3, 队首元素过期, 执行出队操作, deque.removeFirst();
//此时比较队首元素所在数组的值和
//单调递减队列,队列中存储数组下标,如果nums[i]>nums[deque.getLast()]那么deque队列尾部的元素j就要出队deque.removeLast(),因为j<i,并且nums[i]>nums[j],那么往后分析肯定用不到nums[j]。
//deque.addLast();
return res;
}
}
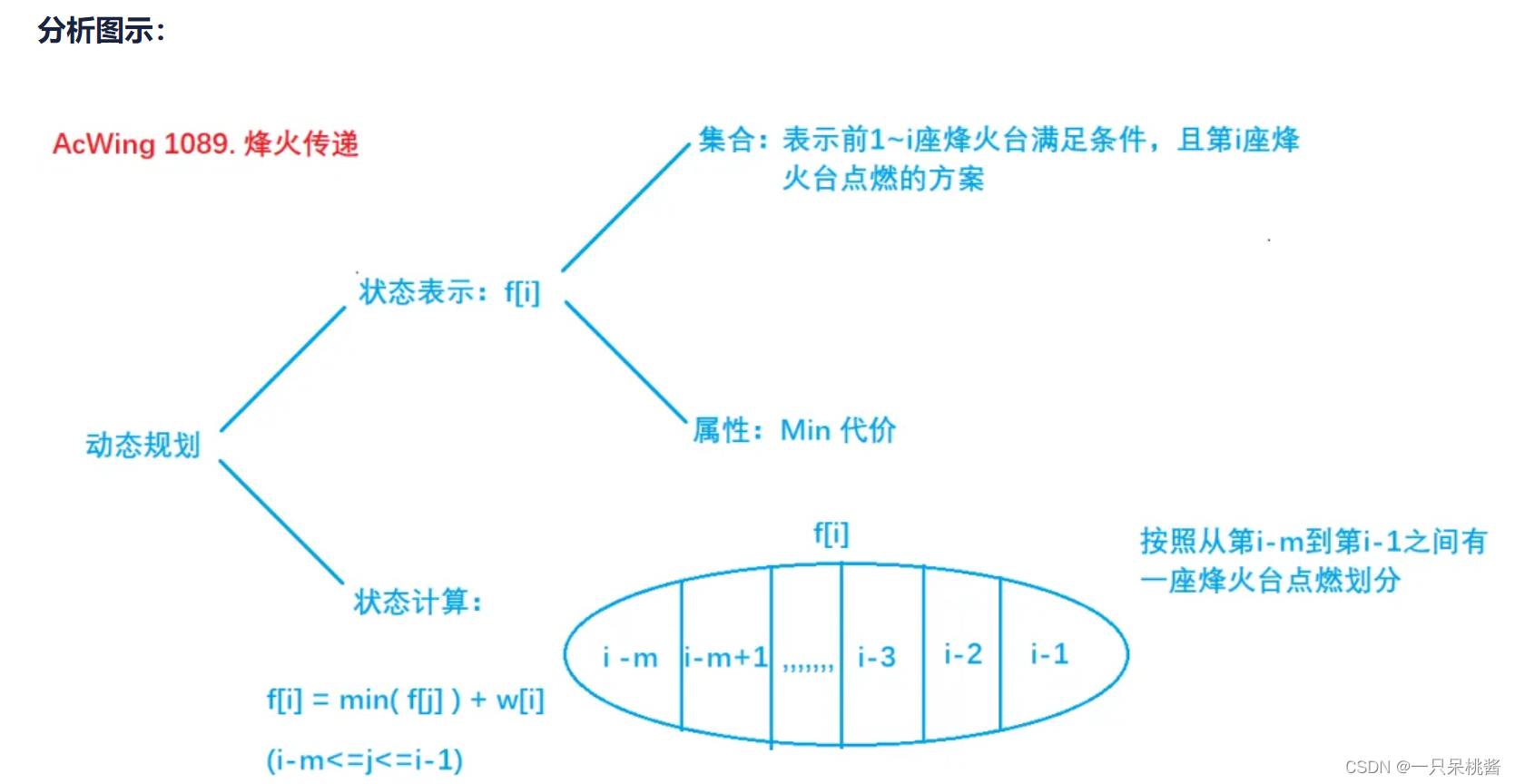
3. 烽火传递
题目描述
原题来自:NOIP 2010 提高组初赛 · 完善程序
烽火台是重要的军事防御设施,一般建在交通要道或险要处。一旦有军情发生,则白天用浓烟,晚上有火光传递军情。 在某两个城市之间有 n座烽火台,每个烽火台发出信号都有一定的代价。为了使情报准确传递,在连续 m 个烽火台中至少要有一个发出信号。现在输入n,m和每个烽火台的代价,请计算总共最少的代价在两城市之间来准确传递情报。
输入
第一行是 n,mn,m,表示 n 个烽火台和连续烽火台数 m;
第二行 nn 个整数表示每个烽火台的代价 ai。
输出
输出仅一个整数,表示最小代价。
样例输入
5 3
1 2 5 6 2
样例输出
4
提示
样例说明
在第 2,52,5 号烽火台上发信号。
题解:
单调队列维护dp
下面主要讲dp思想
设d p [ i ] dp[i]dp[i]表示从i个烽火台开始被点燃的花费最小值
则d p [ i ] = m i n ( d p [ i ] , d p [ j ] + a [ i ] ) ( i − m < = j < = i ) dp[i]=min(dp[i],dp[j]+a[i])(i-m<=j<=i)dp[i]=min(dp[i],dp[j]+a[i])(i−m<=j<=i)根据条件( i − m < = j < = i ) (i - m <= j <= i)(i−m<=j<=i)可知这是一个区间求单调递增队列问题

代码
public class Test {
public int test(int[] fees, int m) {
//fees={0,1,2,5,6,2}, m=3;
//记录窗口内最大值和其位置,每次移动后需要比较窗口内最大值和新值之间的关系
int n=fees.length;
if(m==1){
return Arrays.stream(fees).sum();
}
Deque<Integer> deque=new ArrayDeque<>();
int[] dp=new int[n];
dp[0]=fees[0];
deque.addFirst(0);
for(int i=1;i<n;i++){
while(!deque.isEmpty()&&(i-deque.getFirst()>m)) deque.removeFirst();
dp[i]=dp[deque.getFirst()]+fees[i];
while(!deque.isEmpty()&&deque.getLast()>fees[i]) deque.removeLast();
deque.addLast(i);
}
//两个城市之间有 n 座烽火台,每个烽火台发出信号都有一定的代价,为了使情报准确传递,在连续 m 个烽火台中至少要有一个发出信号。
// f [i] = min( f[j] ) + w[i] (i-m<=j<=i-1) f[i]表示前1-i座均满足要求,最后一座被点燃的是第i座
//用单调递增队列去维护f[j] (i-m<=j<=i-1),每次取队首元素
//维护单调递增队列,首先去除f[j]且j<i-m的数据,然后更新f[i],最后维护单调递增去除队尾元素大于f[i]的,最后将f[i]入队尾
int ans=Integer.MAX_VALUE;
for(int i=n-m;i<n;i++){
ans=Math.min(dp[i],ans);
}
return ans;
}
}