目录
- 三、极限的计算
- 概括
- (1)利用四则运算法则求极限
- 常用的结论(***)
- 未定式的分类以及做法(***)
- **例33 (93 数三)注意负无穷**
- (2)利用两个重要极限求极限
- (3)利用等价无穷小替换求极限
- 不可用洛必达(需要连续)
- 例40.1
- 例42(无穷个无穷小的和不一定为零)
- 例43(拉氏定理的应用)
- 例46(极限拆分,拆出的极限存在才可拆)
- 例50
- 例52(去极限号)
- (4)利用洛必达法则求极限
- 例53(凑等价无穷小)
- 例55(数列函数极限转换,替换n和x的目的是让解题简单)
- 例56(泰勒)
- 例64(抓大头,>>注意趋于无穷)
- 例65(包含抽象函数本身)
- 总结
三、极限的计算
概括
在微积分中,极限是一种重要的数学概念,用于描述函数在某一点或无穷远处的趋势。在计算极限时,可以使用以下四个方法:
-
四则运算法则(Arithmetic Operations Rule):根据四则运算的性质,可以将一个复杂的极限表达式拆解为多个简单的极限表达式,并利用已知的极限结果进行计算。例如,可以将一个极限表达式拆解为两个函数的和、差、积或商,并分别计算它们的极限。
-
无穷小替换法则(Substitution Rule):当计算极限时,可以将一个无穷小量替换为它的极限值。例如,如果一个极限表达式中包含一个无穷小量,可以将该无穷小量替换为它的极限值,从而简化计算过程。
-
重要极限法则(Limit Laws):这是一组用于计算常见函数的极限的法则。包括常数函数的极限、幂函数的极限、指数函数的极限、对数函数的极限、三角函数的极限等。根据这些法则,可以直接计算常见函数的极限,而不需要通过极限的定义进行推导。
-
洛必达法则(L’Hôpital’s Rule):洛必达法则用于计算形如"0/0"或"∞/∞"形式的不定型极限。根据洛必达法则,如果一个极限表达式满足某些条件,可以对该极限表达式中的分子和分母同时求导,并计算它们的极限。洛必达法则能够解决一些复杂的极限计算问题。
这些方法在计算极限时非常有用,能够简化计算过程并得到准确的结果。然而,需要注意的是,在应用这些方法时需要满足一定的条件,并且要谨慎处理不定型极限,以确保计算的准确性。在实际计算中,可以根据具体情况选择合适的方法来计算极限。
(1)利用四则运算法则求极限

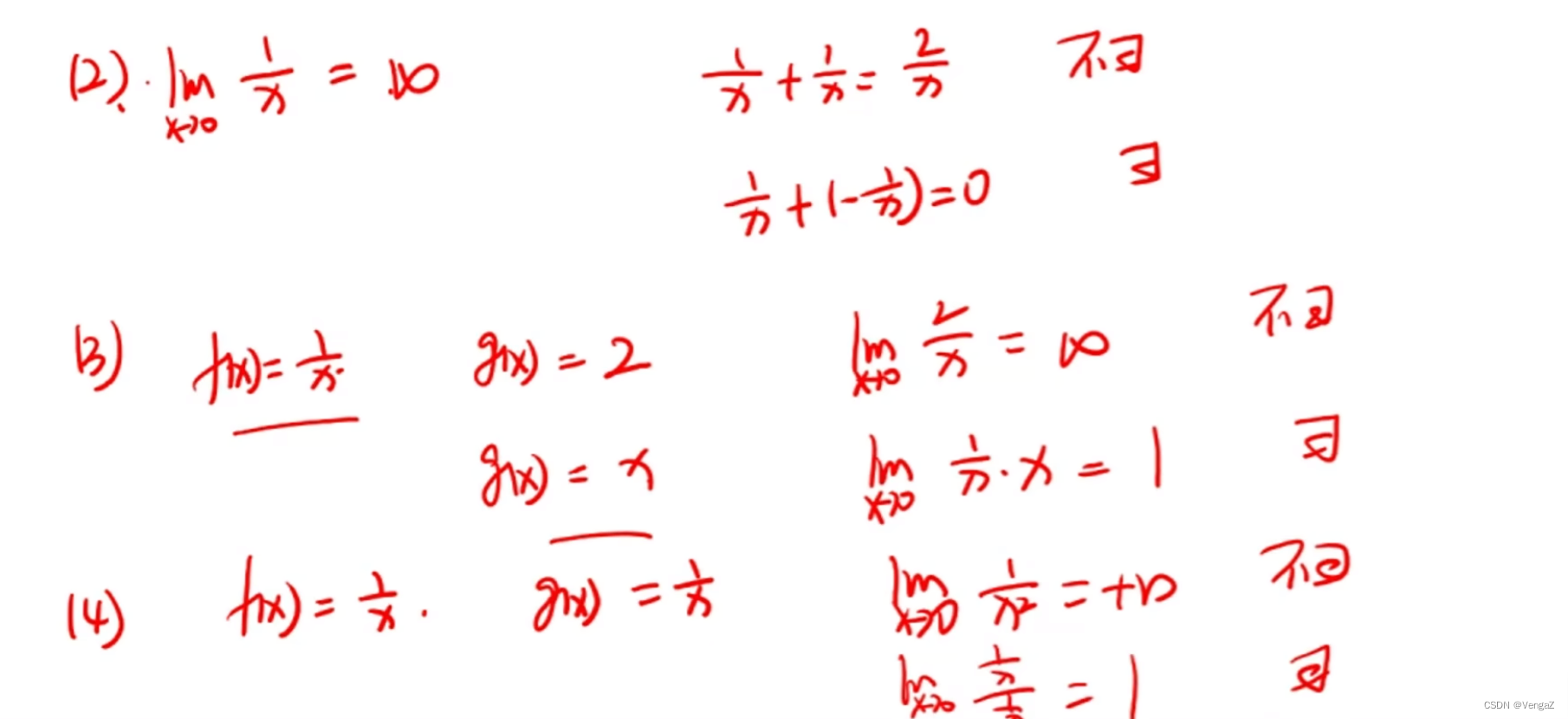

常用的结论(***)

重要结论:
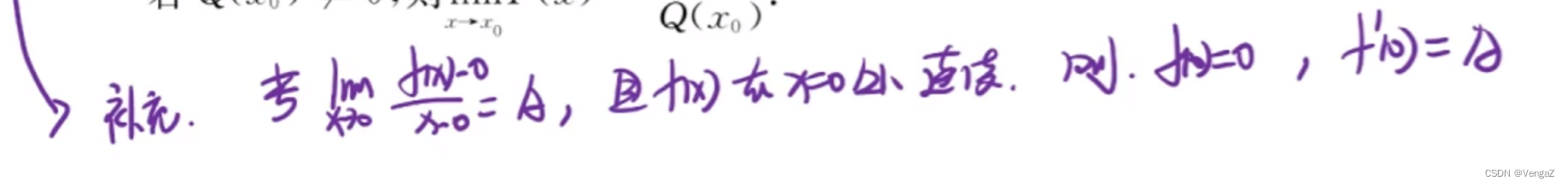
未定式的分类以及做法(***)
0/0的未定式采用
- 洛必达
- 等价替换
- 泰勒
- 拉氏
- 导数定义
无穷加减无穷的
- 遇到分式,通分
- 遇到根式,有理化
- 实在不行,倒带化
- 倒带化本质,提最高次
无穷比无穷
- 洛必达
- 抓大头
- 提最高次
- 同除最高次
1的无穷次方
- 利用第二重要极限
- 幂指转换
例33 (93 数三)注意负无穷

(2)利用两个重要极限求极限


(3)利用等价无穷小替换求极限
乘法随便换,加减要注意(不能抵消)

不可用洛必达(需要连续)
但是这题是数列,不连续

使用海因定理就可以洛必达了
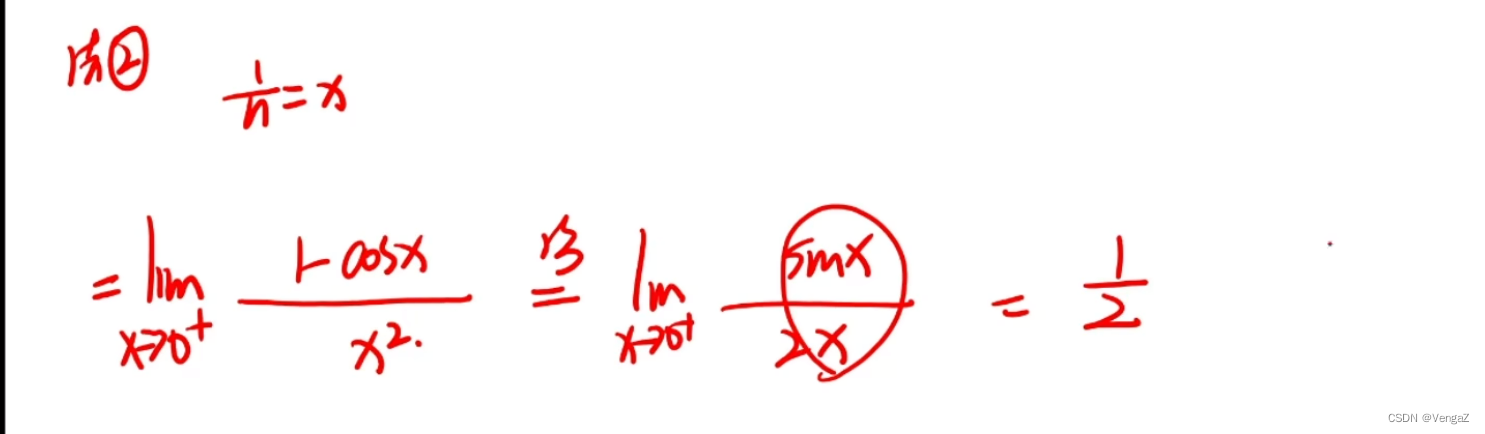
例40.1

例42(无穷个无穷小的和不一定为零)

这个经典错误,是因为忽略了无穷个n的次方的和,直接抓大头,但是这边是无穷个,所以需要特别注意。
例43(拉氏定理的应用)
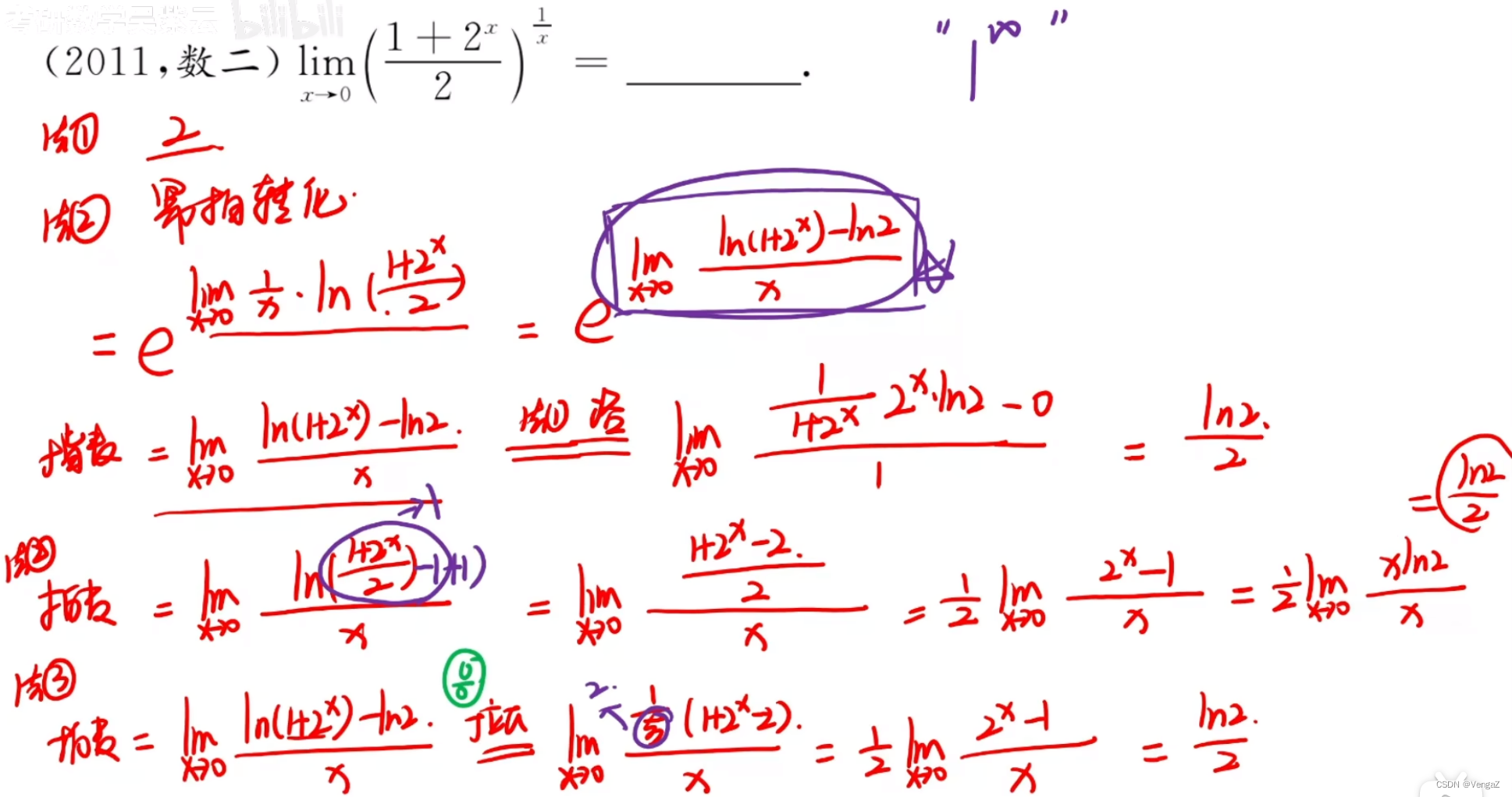
例46(极限拆分,拆出的极限存在才可拆)
1. 只要拆的存在,剩下的不存在,也能拆
2. 整体存在,拆出的两个一定都存在


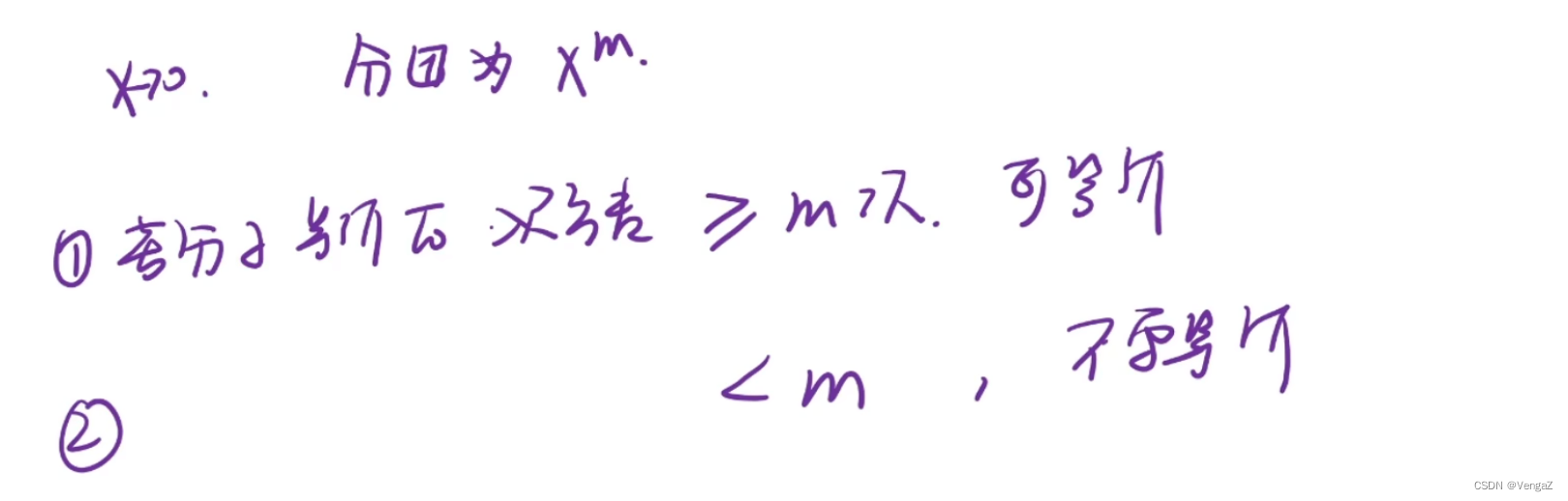
例50

例52(去极限号)

(4)利用洛必达法则求极限

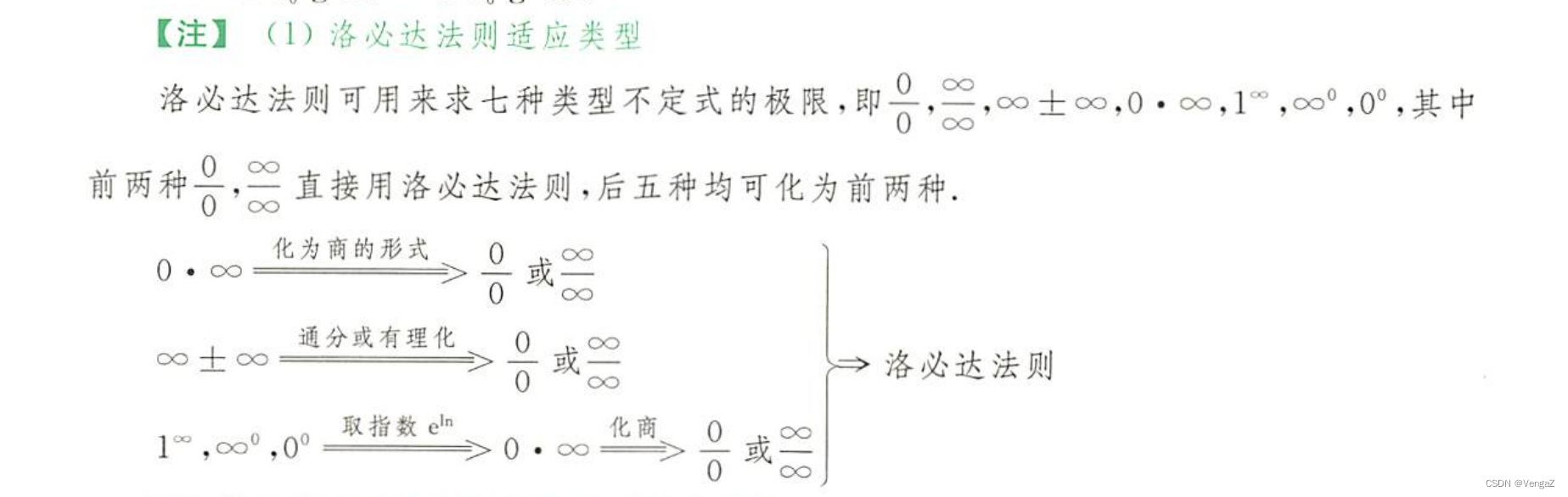
注意用前化简
例53(凑等价无穷小)

例55(数列函数极限转换,替换n和x的目的是让解题简单)

妙解
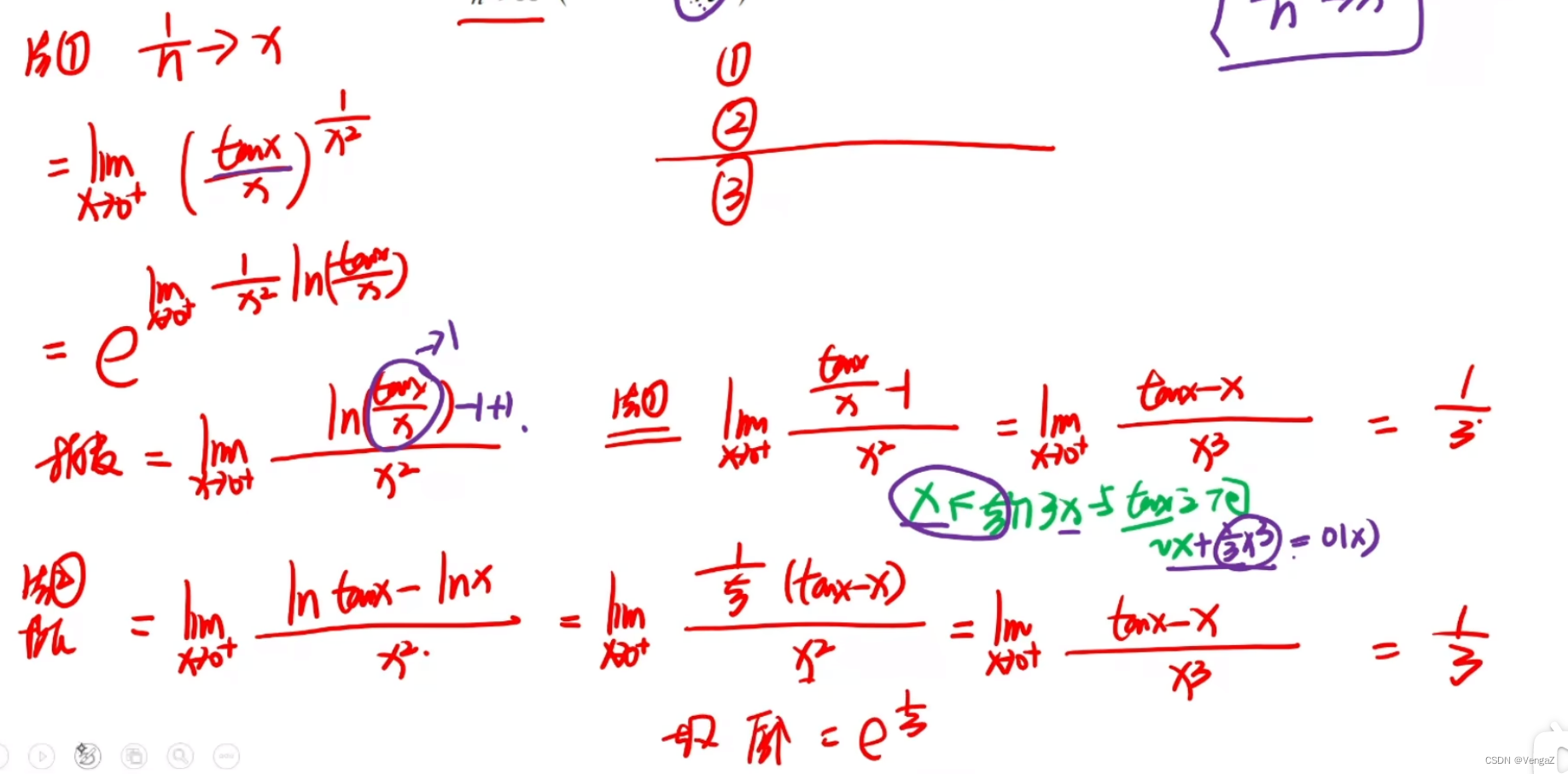
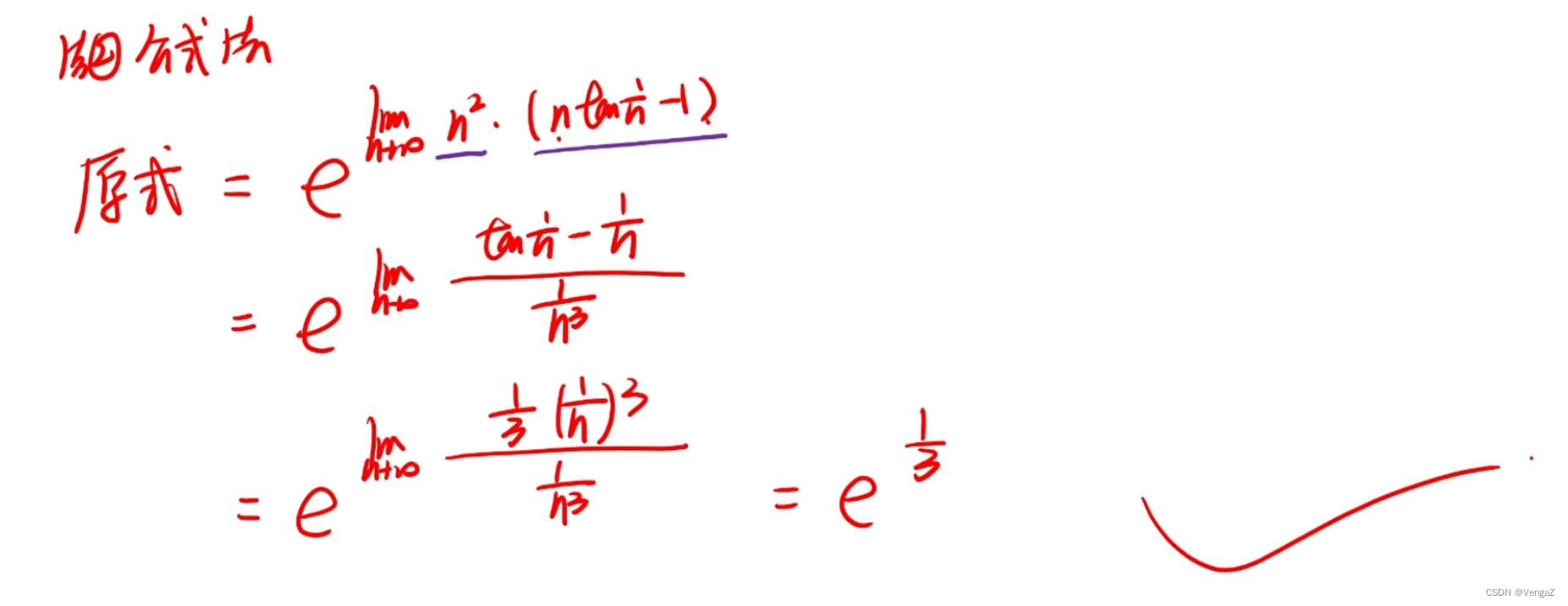
例56(泰勒)

例64(抓大头,>>注意趋于无穷)

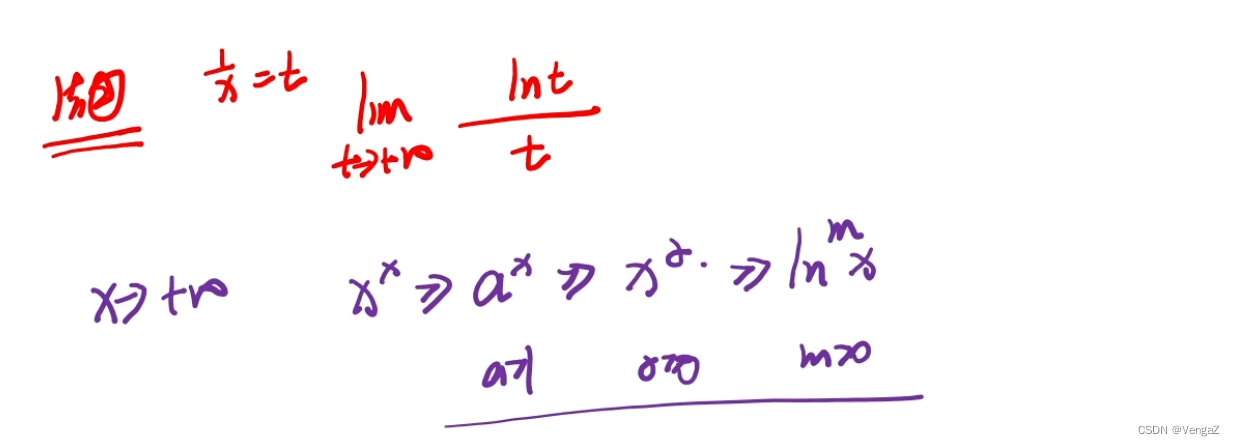
例65(包含抽象函数本身)
法一
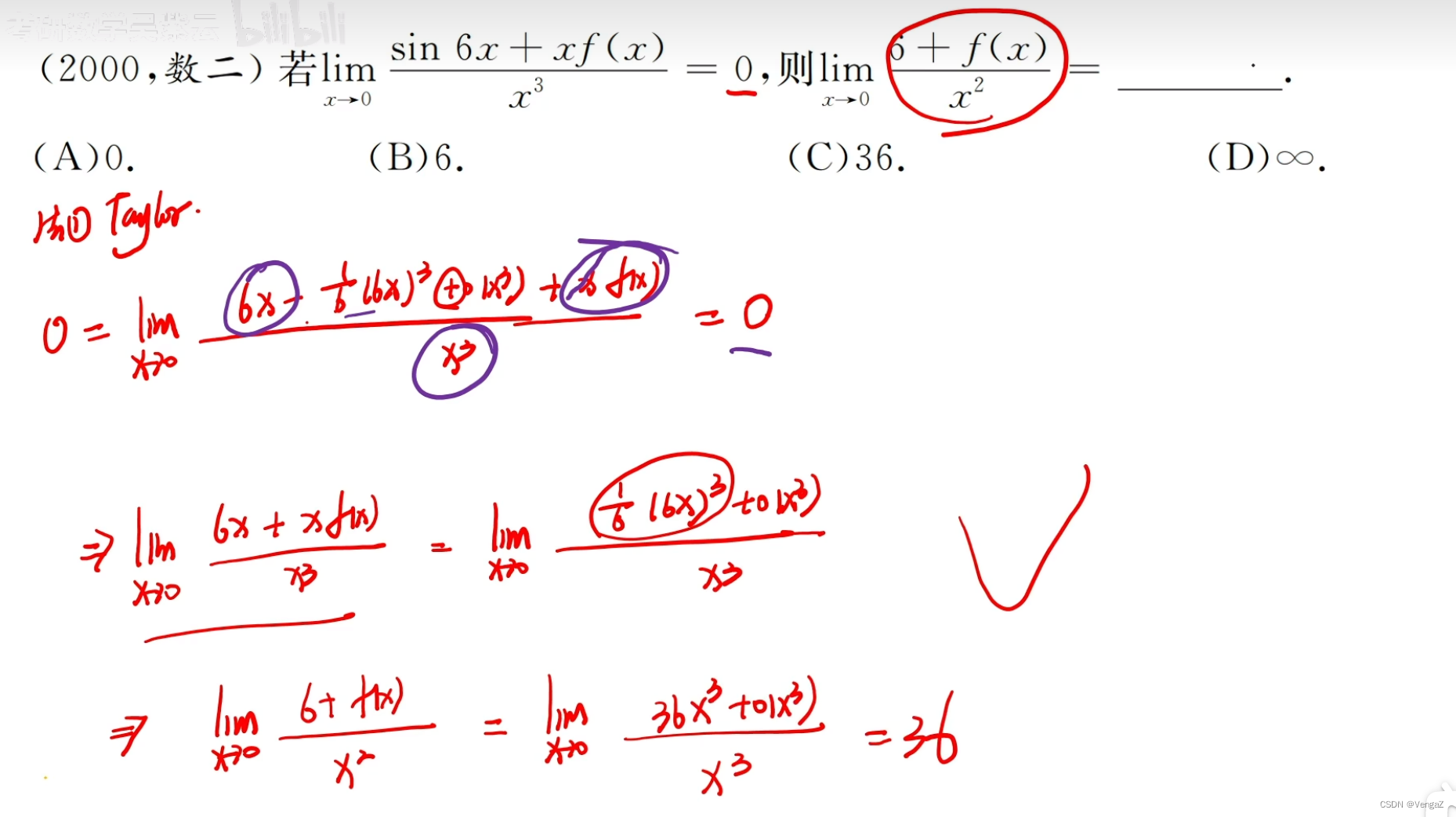
法二
这么凑的原因没有体现
下面说明一下
因为如果把右边的式子与左边的关联起来,就需要上下同乘x,并且分子加上,然后就能把零去掉,得到答案(类似法三,法二法三其实类似的)

法三

法四
这里需要注意脱极限号时需要考虑的去心邻域
思路:
让f(x)不再抽象,直接化为具体,再写出需要求出的式子,然后得出答案
属于无脑做法

总结
在数学中,极限是一种重要的概念,用于描述函数或数列在某个点或无穷远处的趋势。计算高数极限是解决数学问题和应用数学的基础,它涉及到一系列的技巧和方法。以下是一些关于高数极限计算的常见方法和技巧:
-
代入法:当计算极限时,我们可以尝试将变量代入函数中,然后计算当变量趋近于某个值时的函数值。这种方法适用于简单的函数和特定的极限情况。
-
基本极限公式:高数中有一些常用的基本极限公式,如常数的极限、幂函数的极限、指数函数的极限、三角函数的极限等。熟练掌握这些基本公式可以简化极限计算过程。
-
分子分母有理化:当计算含有分式的极限时,可以使用有理化方法,将分子分母进行有理化,从而简化计算。常用的有理化方法包括乘以共轭式或使用特定的代数公式。
-
利用夹逼定理:夹逼定理是计算极限中常用的方法之一。它的基本思想是找到一个比函数小但趋近于极限的函数和一个比函数大但趋近于极限的函数,通过夹逼函数的性质来确定极限值。
-
极限的分解和合并:有时候,可以将复杂的函数进行分解或合并,以便更容易计算极限。这涉及到函数的分解、合并、拆分等技巧,以便简化计算过程。
-
L’Hôpital法则:L’Hôpital法则是一种用于计算某些特定形式的极限的方法。它基于导数的概念,通过求导数来简化复杂的极限计算过程。
除了上述方法和技巧,高数极限计算还需要对数学理论和概念有深入的理解。掌握极限的定义、性质和运算规则,以及对函数的图像、性质和特点有良好的理解,可以帮助我们更好地进行极限计算。
需要注意的是,高数极限计算可能涉及到一些复杂的数学理论和技术,对于特定的问题可能需要更高级的数学工具和方法。因此,在进行高数极限计算时,建议结合具体的问题和学习教材,灵活运用不同的计算方法和技巧,以达到准确和高效地求解极限的目的。